nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: Radically Elementary Category Theory
Bottom of Page1 to 82 of 82
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeMar 21st 2010
- (edited Apr 11th 2010)
One of my all-time favorite books is:
Radically Elementary Probability Theory
Edward Nelson (1987)
Preface:
More than any other branch of mathematics, probability theory has developed in conjunction with its applications. This was true in the beginning, when Pascal and Fermat tackled the problem of finding a fair way to divide the stakes in a game of chance, and it continues to be true today, when the most exciting work in probability theory is being done by physicists working on statistical mechanics.
The foundations of probability theory were laid just over fifty years ago, by Kolmogorov. I am sure that many other probabilists teaching a beginning graduate course have also had the feeling that these measure-theoretic foundations serve more to salve our mathematical consciences than to provide an incisive tool for the scientist who wishes to apply probability theory.
This work is an attempt to lay a new foundations for probability theory, using a tiny bit of nonstandard analysis. The mathematical background required is little more than that which is taught in high school, and it is my hope that it will make deep results from modern theory of stochastic processes readily available to anyone who can add, multiply, and reason.
What makes this possible is the decision to leave the results in non-standard form. Nonstandard analysts have a new way of thinking about mathematics, and if it is not translated back into conventional terms then it is seen to be remarkably elementary.
Mathematicians are quite rightly conservative and suspicious of new ideas. They will ask whether the results developed here are as powerful as the conventional results, and whether it is worth their while to learn nonstandard methods. These questions are addressed in an appendix, which assumes a much greater level of mathematical knowledge than does the main text. But I want to emphasize that the main text stands on its own.
In it, he develops large swaths of probability theory using finite probability spaces.
In the preface above, I wish there was a text in which “probability theory” were replaced by “category theory”.
I honestly think that much of category COULD be understood with “little more [mathematical background] than that which is taught in high school.
Should we make a project of it? Create a reference in the same spirit as Nelson’s text?
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeMar 21st 2010
I disagree wholeheartedly. I mean, I'm probably one of the most extreme in terms of my preference for learning machinery without any motivation, but you really need to have some experience with algebra to get a decent grasp even on ordinary category theory, in my opinion.
-
- CommentRowNumber3.
- CommentAuthorEric
- CommentTimeMar 21st 2010
I take that to mean you won't be volunteering for the project :)
-
- CommentRowNumber4.
- CommentAuthorHarry Gindi
- CommentTimeMar 21st 2010
I'm saying that highschool students have a hard time understanding the definition of a group or a topological space if they haven't had any mathematical training. If those concrete things are too abstract, how could you ever hope to motivate category theory?
-
- CommentRowNumber5.
- CommentAuthorTim_Porter
- CommentTimeMar 21st 2010
If the aims of the project are to explain at an elementary level, choosing a particular audience will influence the choice of examples. I have done this with Biologists but they were used to thinking in terms of systems of interacting objects so ..... The experience was interesting and fruitful. The questions asked were searching and often difficult to answer.
I think that Nelson's book used non-standard analysis to make things simpler i.e. an intuition. Where Harry is right is that unless one finds a similar intuition for category theory then such a project would not be that successful. As to the definition of a group or a space, I think the first point is to get the ideas across not the definitions which should be a later step.
-
- CommentRowNumber6.
- CommentAuthorEric
- CommentTimeMar 21st 2010
Maybe it would actually be easier to understand a group or topological space, if they already understood "arrow theory'. In high school, I would probably call it "arrow theory" because "category theory" sounds intimidating.
Who couldn't understand manipulating a bunch of arrows? You can make games out of it. I'm sure John could figure out a clever way to teach arrow theory to (motivated) high school kids :)
-
- CommentRowNumber7.
- CommentAuthorEric
- CommentTimeMar 21st 2010
- (edited Mar 21st 2010)
Hi Tim,
The audience I had in mind is the same audience that might appreciate Nelson's book, e.g. me :)
To be honest, I have been following this n-community for many many years and there are still lots of basic things I do not understand. This is partially because there does not exist "Radically Elementary Category Theory". I think I should be able to understand most of the stuff, but don't. For example, Kan extension. I still do not have a clue about Kan extension, but I think it is important for physics, see e.g. An Exercise in Kantization.
My motivation is selfish, but I think such a project would be helpful to a lot of people. Especially given that the physics community seems to be showing increased interest in the subject.
-
- CommentRowNumber8.
- CommentAuthorTim_Porter
- CommentTimeMar 21st 2010
@Eric Without trying to sell it to you (I do not get royalties from Dover) in my book on Shape theory (with Cordier) we tried to use the intuitions of general spaces and polyhedra to get across ideas of Kan extensions. Given a general space singular cohomology is sort of trying to get approximations from maps of polyhedra into the space, whilst Cech cohomology is approximating by maps from the space into polyhedra. If you understand Cech theory you can use it as a lever for getting at Kan extensions. We have a notion of Cech extension for functors and relate it to Kan extensions.
-
- CommentRowNumber9.
- CommentAuthorHarry Gindi
- CommentTimeMar 21st 2010
- (edited Mar 21st 2010)
@Tim: If you don't get royalties, why don't you wink wink nudge nudge "release it into the wild", so to speak. If you're interested in more people reading it and you don't get paid anyway, I can't see why you wouldn't (although this is the first time I've ever talked to someone who has authored a book about copyright infringement).
-
- CommentRowNumber10.
- CommentAuthorTim_Porter
- CommentTimeMar 21st 2010
- (edited Mar 21st 2010)
I do not have a latex version. It was published quite a time ago and went out of print. Dover bought up the copyright and made a new version which sells at $11.66 on Amazon. Dover's system is they pay a one off sum to the author that is that. This I like because you don't have dribs and drabs of money coming in. It also means that if they want to make a profit it is up to them. With other publishers there seems flagging interest in selling the book after a very short time. ($12 is not a fortune!)
-
- CommentRowNumber11.
- CommentAuthorEric
- CommentTimeMar 21st 2010
I put it on my Amazon wishlist, but the shipping to HK would cost more than the book, so I'll wait until I can combine it with another order or try to find it in a bookstore here :)
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeMar 21st 2010
Basic notions of category theory, (namely category, functor, natural transformation and then adjoint, and limit and Kan extension) are elementary. All they require is, implicitly, some basic set theory and reason.
This is different from the Kolmogorv foundation of probability theory, which requires measure theory.
I am all in favor of having more elementary explanation of these concepts at our entries. Somebody should just do it. I can offer help, but need to know where help is needed.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeMar 21st 2010
- (edited Mar 21st 2010)
We should go through these items one by one and make sure that the entries contain explanations that make them seem entirely obvious.
Let's start with
and then dip our toes into
As far as just the definitions go, this is all elementary and hence should have an elementaty explanation. In as far as our entries fail to give this, we should improve them. So let's play a little question-and-answers game with these entries to improve them: you ask questions about aspects that are not clear, we answer them by working answers into the entries.
-
- CommentRowNumber14.
- CommentAuthorEric
- CommentTimeMar 21st 2010
The entry on category is fine, although it is sadly lacking in pictures. All of category theory, which could be called "arrow theory", is begging to be drawn. The fact there are no pictures is a big hole.
The entry on functor is "ok", but I am not personally 100% ok with the concept. Evidence of my confusion can be found many places, e.g. functor (discussion), Natural Transformation (ericforgy), etc. For the record, I don't going around proposing new definitions for fun. I tried hard to understand functor and couldn't. The way I know I understand something is when I can express it in my own way. That hasn't happened with functor yet.
The "concept" of what natural transformation is trying to say is clear, but I could not get myself to accept the standard definition. Why should it be restricted to functors sharing the same domain and codomain? That seems to me to illustrate a clear (an unsavory) bias to bigons. A natural transformation should encompass maps between functors with any domain and codomain.
For example, given two categories C and D, we can obtain a functor category [C,D], but the more interesting thing to look at in my opinion is Arr(Cat), i.e. the arrow category of categories. Since the morphisms in Cat are functors, the objects in Arr(Cat) are functors. So I think a better way to think of natural transformations are as morphisms in Arr(Cat). The standard definition of natural transformation would then correspond to "parallel" morphisms in Arr(Cat). In fact, before I started actually looking closer at the definition of natural transformation, this is what I thought they were all this time, i.e. morphisms in Arr(Cat).
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeMar 21st 2010
The entry on functor is "ok", but I am not personally 100% ok with the concept. Evidence of my confusion can be found many places,
Yes, I know. So we need to work on this. concretely. Let's do it.
I am puzzled by what you are puzzled about . You understand the notion of a homomorphism (of groups, say).
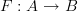 is a homomorphism if for all
is a homomorphism if for all 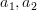 in A we have
in A we have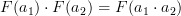 .
.Here on the left the dot is multiplicaion in A, on the right it is multiplicaiton in B.
Okay?
A functor is precisely the same thing, only that A and B are allowed to be categories. The dot now means composition of morphisms in A and in B, respectively.
This is elementary. If the explanation still does not work, it means there is some other kind of language problem here. Let's sort it out.
Last time that we discussed this it was you who drove the discussion away from being elementary. You started talking about graphs of functors and the like, and everyone here started commenting on that, making the discussion ever more advanced. I suspect it would be better if we really just sort out the simple elementary definition of functor and natural transformation first.
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeMar 21st 2010
The "concept" of what natural transformation is trying to say is clear, but I could not get myself to accept the standard definition.
I am willing to discuss non-standard definitions as soon as we are all on the same page concerning the standard definitions. We can't do elementary category theory and speculative category theory at the same time.
-
- CommentRowNumber17.
- CommentAuthorIan_Durham
- CommentTimeMar 21st 2010
I'll toss my two cents in on this one since I'm in the process of teaching myself category theory and since I teach undergrads. I really like Steve Awodey's book. His first chapter is almost radically elementary.
I agree partly with Harry, but given the types of homework problems my kids come home with (they're in first and third grades at a public school in a semi-rural district), today's students should be able to get it. -
- CommentRowNumber18.
- CommentAuthorDavidRoberts
- CommentTimeMar 22nd 2010
>So I think a better way to think of natural transformations are as morphisms in Arr(Cat). The standard definition of natural transformation would then correspond to "parallel" morphisms in Arr(Cat). In fact, before I started actually looking closer at the definition of natural transformation, this is what I thought they were all this time, i.e. morphisms in Arr(Cat).
and this is how you think of a double category. If you throw a natural transformation (the ordinary sort) into the square, you get what Ehresmann called the double category of quintettes Q(Cat) associated to the 2-category Cat. Then Cat is a sub-double category of Q(Cat) -
- CommentRowNumber19.
- CommentAuthorMike Shulman
- CommentTimeMar 22nd 2010
I don't have much to add to this, but I would like to point out that the radically in Nelson's title indicates that he is doing things in a totally different (and, at least arguably, more elementary) way from the vast majority of probability theorists, and in his case that is made possible by the tools of nonstandard analysis. While I'm all in favor of making category theory more comprehensible to the newcomer, I don't think that in this case there is any such "power tool" out there which can "radically" transform it to make it easier to understand. You really have to understand the motivating examples in order for category theory to make sense.
-
- CommentRowNumber20.
- CommentAuthorHarry Gindi
- CommentTimeMar 22nd 2010
@Ian: Did you ever take my advice about reading up on Topology? Surely that would be more important for a physicist than category theory regardless of the field in which said physicist works. I'd just like for you to consider that (I'm sure most other people would agree).
-
- CommentRowNumber21.
- CommentAuthorEric
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
<p>When it comes to functors, I think one thing that confuses me is something Toby mentioned <a href="https://ncatlab.org/nlab/show/functor+%28discussion%29">here</a>, i.e. the difference between <img src="/extensions/vLaTeX/cache/latex_7c29dd72c47018a1ce08a50ea116e0f6.png" title="\mapsto" style="vertical-align:-20%;" class="tex" alt="\mapsto" /> and <img src="/extensions/vLaTeX/cache/latex_164bbd9e6c19b06e40e853c61daee542.png" title="\to" style="vertical-align:-20%;" class="tex" alt="\to" />. We learn that morphisms are arrows between objects, so for a functor, maybe I expect/want an arrow</p> <img src="/extensions/vLaTeX/cache/latex_216fdbfffb9b8f566c68068c0c749067.png" title="x\to F(x)." style="vertical-align:-20%;" class="tex" alt="x\to F(x)." /> <p>This way, the standard definition could follow from saying something like "blah blah blah such that all diagrams commute".</p> <p>For example, if a functor came with actual component morphisms</p> <img src="/extensions/vLaTeX/cache/latex_a9482520eeefa75cfbb7d3458e6bbcba.png" title="\alpha_x: x\to F(x)" style="vertical-align:-20%;" class="tex" alt="\alpha_x: x\to F(x)" /> <p>and</p> <img src="/extensions/vLaTeX/cache/latex_ff0b4d356e3e1861a9b7873a0e332fa0.png" title="\alpha_y: y\to F(y)" style="vertical-align:-20%;" class="tex" alt="\alpha_y: y\to F(y)" /> <p>then the condition</p> <img src="/extensions/vLaTeX/cache/latex_c4f1737823f26473b9e2497837a6982a.png" title="F(f\circ g) = F(f)\circ F(g)" style="vertical-align:-20%;" class="tex" alt="F(f\circ g) = F(f)\circ F(g)" /> <p>would follow if all diagrams</p> <img src="/extensions/vLaTeX/cache/latex_6cf86a4f2f3d78bca1c221df450bcd6d.png" title="\array{ x & \stackrel{f}{\to} & y \\ \mathllap{\scriptsize{\alpha_x}}\downarrow && \downarrow\mathrlap{\scriptsize{\alpha_y}} \\ F(x) & \stackrel{F(f)}{\to} & F(y) }" style="vertical-align:-20%;" class="tex" alt="\array{ x & \stackrel{f}{\to} & y \\ \mathllap{\scriptsize{\alpha_x}}\downarrow && \downarrow\mathrlap{\scriptsize{\alpha_y}} \\ F(x) & \stackrel{F(f)}{\to} & F(y) }" /> <p>commute.</p> -
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
There are some ways to answer this, for instance in terms of functors that come equipped with a natural transformation from the identity functor.
But somehow I feel before getting into variations of standard definitions, it would serve to just sort the standard definitions out. The standard notions of category, functor and natural transformations are GoodDefinitions™ and we are not going to change them. They induces loads of related concepts, and I think this will cover everything you will ever come up with.
So it is of importance that we base everything on a clear understanding of the standard definitions of category/functor/natural-transformation.
The motivating example of a functor that you should keep in mind is that enocding a linear representation of a one-objecct groupoid.
Let G be a group,
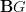 the corresponding one-object category and let
the corresponding one-object category and let 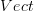 be the category of vector spaces. Then functors
be the category of vector spaces. Then functors 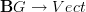 are precisely linear representations of the group G.
are precisely linear representations of the group G.Looking at this example should entirely clarify why the notion of functor is the way it is. This might also be a good test case to check what other definitions that you can dream up will look like.
-
- CommentRowNumber23.
- CommentAuthorHarry Gindi
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
@Eric: Remember that functors go between categories, so talking about morphisms between objects in two categories does not make sense (at least almost never, since you can look at natural transformations between endofunctors, but that's totally unimportant for this discussion). To specify a functor, you're specifying a function between sets (classes) of objects:
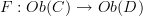
and a family of functions indexed by pairs of objects:
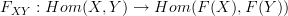 for all
for all  and
and 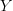 in
in 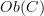 satisfying the compatibility condition:
satisfying the compatibility condition: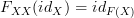
and the cocycle condition on morphisms (Let
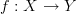 and
and 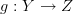 ).
).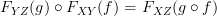 .
.(Unfortunately due to notation, this doesn't look like a cocycle condition because we write composition of morphisms backwards, but it is in fact a cocycle condition).
(Note that all uses of composition in this post are technically abusing notation, because composition is defined as a map between products of hom sets for each category. In the notation I will introduce in a moment, we take the same notational liberties.)
If we wanted to be cool guys and compose on the right, we could restate that as
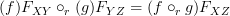 ,
,where
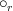 denotes reverse order composition. In this notation, the cocycle condition now becomes apparent.
denotes reverse order composition. In this notation, the cocycle condition now becomes apparent.There's quite a bit more nuance to this when we're talking about enriched functors between enriched categories, but in the case of ordinary functors, this works just fine. Enriching in categories where the objects do not have sets of points, however, is quite difficult, because you can't actually talk about actual morphisms in your enriched category.
Yes, there are weakenings to these conditions as well see for example pseudofunctor.
Now the definition you've got is almost right, but in fact, what Toby is saying that what you're doing wrong is trying to induce morphisms between categories, which makes no sense (as mentioned above). What Toby is saying to you is that you can describe the function
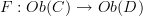 componentwise (since it's a function) as the function sending
componentwise (since it's a function) as the function sending 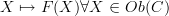 .
.I get the feeling that you're trying to pretend that the set of objects and the hom-sets aren't actually sets. If this is the case, remember that being overly cautious about evil is very likely to paralyze you. Sets are awesome and trying to avoid them whenever possible is a mistake. (Yes, I realize that this does not extend to the enriched case, but you have no business worrying about enriched categories and functors before you understand ordinary categories.)
-
- CommentRowNumber24.
- CommentAuthorIan_Durham
- CommentTimeMar 22nd 2010
@Harry: It is indeed on my extensive "to do" list. I've been out of town so I haven't had a chance to drop by the library yet, but hopefully this week I will get the time. I'm doing some stuff on closed timelike curves (yes, it's nuts, but I'm not the only one) and it will likely be very useful for that. -
- CommentRowNumber25.
- CommentAuthorHarry Gindi
- CommentTimeMar 22nd 2010
There are places on the internet where you can get the book for free...
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
Thanks, Harry, I suppose what you said is useful. To the extent that it isn't there yet, how about adding some of this to the entry on functor.
-
- CommentRowNumber27.
- CommentAuthorEric
- CommentTimeMar 22nd 2010
@Eric: Remember that functors go between categories, so talking about morphisms between objects in two categories does not make sense
@Harry: But as we discussed here, those morphisms do make sense in the cograph.
So I guess I'm picking up where we left off there. Given a functor, we obtain a cograph. Can we construct a functor given a cograph? Is this, in fact, a reasonable way to define a functor? I think somewhere Urs said it is.
-
- CommentRowNumber28.
- CommentAuthorHarry Gindi
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
If you do not understand functors, you should not be thinking about cographs, that's like trying to fly a plane before you can walk.
I do not think that you are being reasonable here. The notion of a functor that I just described is morally a "homomorphism" of morphisms. It fixes the identity (identities) and commutes with the operation (only morally, because there are some minor problems with defining it this way [this definition does not actually make sense formally]).
-
- CommentRowNumber29.
- CommentAuthorEric
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
I know what a functor is. I understand the definition. I wrote the example section at functor.
My questions are more about the motivations. What is a functor REALLY? I tend to think category theory is more than a convenient tool to calculate stuff and think it "speaks to nature". If spacetime is fundamentally a higher category, what does that REALLY mean?
For that reason, I think it is worthwhile trying to think deeply about "easy" stuff most people tend to take for granted.
For example, I tend to think category theory should ultimately transcend the english language. In a way, it is its own language. Perhaps it might even turn out to be the language of nature and/or of mathematics. If so, it shouldn't need human words to define the most basic constructions. They should be accessible through pictures alone. The standard definition of a functor requires human words, so I don't like it. If there is a way to define functor purely using pictures, I'd be happy. This would be "radical". A high school student could understand this.
It reminds me of one of my favorite thought experiments posed by John. How do you describe a rock without using coordinates? Nature manages to do it. So should we be able to once we find the right language.
-
- CommentRowNumber30.
- CommentAuthorHarry Gindi
- CommentTimeMar 22nd 2010
I don't agree with John's statement. I realize that it was metaphorical, but it still doesn't make sense to me, and I'm pretty sure that I understand what he meant.
-
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
I know what a functor is.
I am glad to hear this, but, you know, maybe as Harry and others, my impression was that you kept saying that you don't follow the definition of what a functor is. But I am relieved to see that this was a misunderstanding, because it kept baffling me.
If there is a way to define functor purely using pictures, I'd be happy. This would be "radical".
So what about the internal definition of functor. That is entirely arrow-theoretic.
In fact, all of category theory may be formulated internally this way, making every single statement an arrow-theoretic statement.
Maybe that's what you are looking for?
-
- CommentRowNumber32.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
Eric, for instance above you said:
I tried hard to understand functor and couldn't.
Maybe you need to clarify what you mean by such sentences.
-
- CommentRowNumber33.
- CommentAuthorEric
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
This might also be a good test case to check what other definitions that you can dream up will look like.
@Urs: Thanks for the challenge. For the record, I have nothing against functors. There are probably an infinite number of ways to define them. I just don't like the standard definition. It's not the concept I have trouble with. I'd be happy to find a different (but equivalent) definition.
In the case of a representation
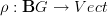 , for each
, for each 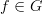 , we'd have a morphism
, we'd have a morphism 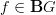 , two components
, two components 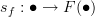 and
and 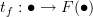 , such that
, such that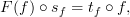
which is simply a statement that the obvious diagram commutes.
Similarly, for any other
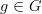 , we also have
, we also have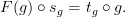
Since any two squares commute, when we compose them, we get a new commuting square
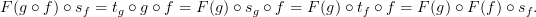
Therefore, on the image
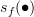 at least, we have
at least, we have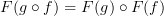
as a consequence of a commuting diagram. Not an axiom put in by hand.
-
- CommentRowNumber34.
- CommentAuthorEric
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
When there is only one object, the calculation actually seems more mysterious, so here is the same thing but in the more general case...
Given categories
 and
and  , for each morphism
, for each morphism 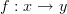 in
in  , a functor
, a functor 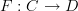 consists of two components
consists of two components 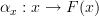 and
and 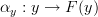 such that the obvious diagram commutes, i.e.
such that the obvious diagram commutes, i.e.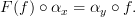
Given another morphism
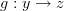 we also have
we also have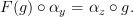
Now turn the crank...
Since composing two commuting squares gives a new commuting square, we have
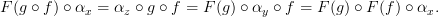
Edit: I like this because it seems to more "naturally" relate to the definition of natural transformation. You can even go the other direction and use something like this to define morphisms so you have a nice ladder of consistent concepts.
-
- CommentRowNumber35.
- CommentAuthorEric
- CommentTimeMar 22nd 2010
Maybe you need to clarify what you mean by such sentences.
@Urs: Sorry. There are different levels of the word "understand". I can recite the definition. I can construct examples. I can teach it to others. But I do not REALLY understand it. I doubt that helped clear things up, but I hope you get what I mean a little bit :)
Maybe that's what you are looking for?
Could be! I will have to have a look. Thanks
-
- CommentRowNumber36.
- CommentAuthorEric
- CommentTimeMar 22nd 2010
I don't agree with John's statement.
@Harry: If you can be so dismissive of one of the most profound statements I've ever heard, then we do not belong in the same conversation :)
I doubt even John meant it to be as profound as I took it to be, but thinking about that question has impacted the way I think about the world.
-
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
two components
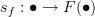
this seems to be the recurring source of confusion. What are these components? Where do they live? I don't understand what you mean here, and I think this is what others kept saying, too.
 is an object in
is an object in 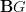 while
while 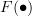 is an object in
is an object in 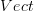 . What do you mean by writing
. What do you mean by writing 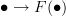 ?? And why do you insist on drawing this?
?? And why do you insist on drawing this?You should think of a category as a directed space. Objects are points, morphisms are paths. A functor is then just a map of spaces, of directed space. You map one into the other. This is supposed to be the most evident operation in the world! I am lacking intuition as to what it is you want to change about it.
-
- CommentRowNumber38.
- CommentAuthorEric
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
this seems to be the recurring source of confusion. What are these components? Where do they live?
We had this same conversation here:
Todd: What I was saying is that wherever these
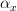 are supposed to live, it’s can’t be in
are supposed to live, it’s can’t be in 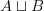 , because in
, because in 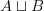 , there simply are no morphisms of that form.
, there simply are no morphisms of that form.Your picture suggests that you have in mind some category C into which A and B embed; it can’t be
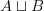 since your
since your 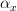 simply don’t exist there.
simply don’t exist there.[snip]
Urs Schreiber: concerning the nature of C: as I suggested before, it does make sense to take this to be the cograph of a functor. And indeed, in some situations it is useful to define the notion of functor in terms of the notion of cograph.
I mean the same thing here that I meant there. If we need to use the word "cograph", then let's if it helps :)
-
- CommentRowNumber39.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
If we need to use the word "cograph", then let's if it helps :)
I'd really rather not. Not in a thread on radically elementary category theory, anyway. And not before you admit that you understand -- in whatever sense of the word -- the plain notion of functor.
Because i feel we keep going in loops without every touching the ground, otherwise. You ask for different perspecives on elementary notions and we try to guess ever more sophisticated concepts that might model this. But we never quite know if we are making progress on communicating basic facts.
You said you wanted to understand Kan extensions. For that I would urge you not to try to think of functors in terms of the cographs. At least not to begin with.
The direct route would be to
first check if we agree on the standard definition of category, functor and natural transformation
and then try to see if we can get agreement on the notion of adjoint functor.
That's crucial for everything that will follow. You need to have a very clear idea of what adjoint functors are. In the standard way of talking about them. You need to feel at home with the standard way to talking about these things before inventing non-standard ways, I think.
-
- CommentRowNumber40.
- CommentAuthorEric
- CommentTimeMar 22nd 2010
<div> <blockquote>The direct route would be to <ul><li>first check if we agree on the standard definition of category, functor and natural transformation</li><li>and then try to see if we can get agreement on the notion of <a href="https://ncatlab.org/nlab/show/adjoint+functor">adjoint functor</a>.</li></ul> That's crucial for everything that will follow.</blockquote> <p>Yep yep. The map is pretty much what I expected. Category and functor are pretty easy to live with even for someone as dense as I am. I spent some time working on natural transformation. That process is actually what led to this train of thought (or chaos?).</p> <p>At this point, I'm pretty ok with the first stop on your route and know the next stop is <a href="https://ncatlab.org/nlab/show/adjoint+functor">adjoint functor</a>. I'm not ready yet to absorb anything you might have to say about that, so let me do some homework first and come back here when I'm ready to ask some questions.</p> </div> -
- CommentRowNumber41.
- CommentAuthorIan_Durham
- CommentTimeMar 22nd 2010
<div> <blockquote><br/>There are places on the internet where you can get the book for free...<br/></blockquote><br/><br/>@Harry: Yes, but I hate reading books and papers on my computer. I like the feel and smell of a good book. :) </div> -
- CommentRowNumber42.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
I'm not ready yet to absorb anything you might have to say about that, so let me do some homework first and come back here when I'm ready to ask some questions.
Okay. We had recently that discussion on the adjunction
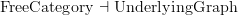 .
.Did you sort that out? Do you see why that is an adjunction?
This is of the kind of general standard examples that would be best to look at, first : free functors left adjoint to forgetful functors.
For instance it is good to convince oneself of the fact that the functor
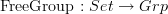 that sends a set to the free group on that set (elements are words in elements of the underlying set and formal inverses of these elements) is left adjoint to the functor
that sends a set to the free group on that set (elements are words in elements of the underlying set and formal inverses of these elements) is left adjoint to the functor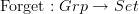
that takes a group and forgets everything except its underlying set.
This kind of stuff we need to eventually say "Kan extension". Because for
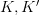 and
and  three categories, and
three categories, and 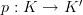 a functor, left and right Kan extension along
a functor, left and right Kan extension along 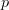 are the left and right adjoint functors to the evident functor of functor categories
are the left and right adjoint functors to the evident functor of functor categories![p^* : [K',C] \to [K, C] p^* : [K',C] \to [K, C]](/extensions/vLaTeX/cache/latex_c96959f50f9d4a5df917c07baa7fee7c.png) .
.So the roadmap towards understanding Kan extension is understanding what these ingredients mean, how
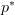 works and then finally what the left and right adjoint functors to
works and then finally what the left and right adjoint functors to 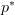 are like.
are like. -
- CommentRowNumber43.
- CommentAuthorHarry Gindi
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
@Urs:
So what about the internal definition of functor. That is entirely arrow-theoretic.
I believe that if we consider a category to be a presheaf on the 1-globe with two distinct edges (only mildly circular!), we can use a similar definition as well.
(And yes, circular was referring both to the reasoning and the 1-globe. =))
-
- CommentRowNumber44.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
So what about the internal definition of functor. That is entirely arrow-theoretic.
I believe that if we consider a category to be a presheaf on the 1-globe with two distinct edges (only mildly circular!), we can use a similar definition as well.
Yes, because that's just a slightly more succinct way of saying "category internal to Set": you encode the three items
object of objects
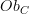
objects of morphism
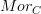
source and target morphisms:
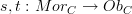
into the single statement:
- functor from
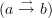 to Set.
to Set.
Yes, you can do that.
You can go further and notice that this is not so much a 1-globe in Set, as a span in Set. Using this you can go further and see that also the rest of the data of an internal category may be phrased this way: an internal category in Set is precisely a span in Set that is a monad in the category of spans.
(Do you see this? This is a pleasing exercise that everyone should do once.)
-
- CommentRowNumber45.
- CommentAuthorHarry Gindi
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
I don't like to talk about "categories internal to (U)-Set", since for me, this is equivalent to saying "(unenriched) (U)-small category", where the (...) denotes words that are left out for convenience. Of course, this is because there is no such thing as the proper class of all sets, because proper classes are not mathematical objects. When we say small, we mean "relatively small" with respect to some fixed universe that we implicitly fixed.
Because all (unenriched) categories have sets of objects and sets of morphisms!
-
- CommentRowNumber46.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
I don't like to talk about "categories internal to (U)-Set",
Fine, you don't need to talk about them if you don't like. Since you started talking about
...a presheaf on the 1-globe with two distinct edges
I thought you wanted to talk about this.
-
- CommentRowNumber47.
- CommentAuthorHarry Gindi
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
Oh, sure, I'm just complaining, don't mind me. I always find what you have to say interesting =)...
I just also like to complain.
-
- CommentRowNumber48.
- CommentAuthorDavidRoberts
- CommentTimeMar 23rd 2010
hopefully in a constructive direction... -
- CommentRowNumber49.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
Did you sort that out? Do you see why that is an adjunction?
Alas, not yet. This is a good homework problem though.
This is of the kind of general standard examples that would be best to look at, first : free functors left adjoint to forgetful functors.
Yeah, I like this. I've read it and believe it, but need to work through examples (like the ones above).
If we need to use the word "cograph", then let's if it helps :)
I'd really rather not.
Why not? I actually thought the cograph perspective would help with adjunctions. I remember you mentioning that somewhere.
Back to the first stop of the route to Kan extensions...
We have objects, morphisms, functors, and natural transformations. These are (as far as I can tell) generally thought to be different things that tie together to make a beautiful story. But I think they are all somehow secretly "the same". The "sameness" of objects and morphisms, I think, is more commonly accepted, e.g. by identifying objects with the identity morphisms, a category is just "all morphisms". What if functors could be thought of as special 2-morphism-like-thingies-of-some-kind?
I guess I'm pulling a Heaviside. Stop worrying about the meaning of
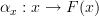 and start computing stuff with it. As I showed above, we get the standard definition of functor as a result of a computation, not a definition thrown in by hand. If these components were somehow placed in a context for which they made sense, then functors can be thought of as special 2-morphism-like-thingies and natural transformations become special 3-morphism-like-thingies. Maybe the context I'm looking for is the cograph context?
and start computing stuff with it. As I showed above, we get the standard definition of functor as a result of a computation, not a definition thrown in by hand. If these components were somehow placed in a context for which they made sense, then functors can be thought of as special 2-morphism-like-thingies and natural transformations become special 3-morphism-like-thingies. Maybe the context I'm looking for is the cograph context?I explained a similar alternative/speculative definition of natural transformation here in terms of "component functors" (the standard definition involves component morphisms).
-
- CommentRowNumber50.
- CommentAuthorDavidRoberts
- CommentTimeMar 23rd 2010
If a notation works for categories, it should work for sets. What is the meaning of
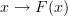 for a function
for a function 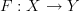 where
where  and
and 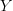 are sets? Is this more or less useful than the usual notation
are sets? Is this more or less useful than the usual notation 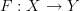 ? I would way less, because it doesn't identify the codomain of
? I would way less, because it doesn't identify the codomain of 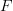 . This feels to me like writing
. This feels to me like writing 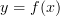 as per first-year calculus notation for a function. Actually it seems more like lambda calculus, but I don't think that introducing such things here would help to grok functors.
as per first-year calculus notation for a function. Actually it seems more like lambda calculus, but I don't think that introducing such things here would help to grok functors. -
- CommentRowNumber51.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
Hi David,
Thanks for your questions. They make me think, which is never a bad thing :)
I'm thinking out loud, but in the case of sets,
 and
and 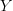 , the first thing to do I suppose is form the category of elements
, the first thing to do I suppose is form the category of elements 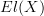 and
and 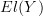 so that elements
so that elements 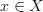 are promoted to objects in in
are promoted to objects in in 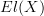 . Since
. Since  and
and 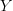 are just sets, there are no non-identity morphisms in
are just sets, there are no non-identity morphisms in 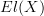 and
and 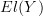 . Then
. Then 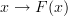 is a morphism in the disjoint union
is a morphism in the disjoint union 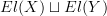 .
.In this case, the fact we are talking about cographs is explicit I think.
Note, when I write
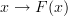 I mean there is literally an arrow from object
I mean there is literally an arrow from object  to object
to object 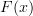 .
.Actually it seems more like lambda calculus, but I don't think that introducing such things here would help to grok functors.
Why not? Lambda calculus seems very natural to me. In fact, I've been using it for years on a daily basis (without explicitly knowing it) in my "real life" :)
Not a day goes by I don't write at least one anonymous function. My weapon of choice is Matlab, so the syntax is different than traditional lambda calculus, but the concepts are similar.
-
- CommentRowNumber52.
- CommentAuthorDavidRoberts
- CommentTimeMar 23rd 2010
I think people would be less confused all round if we all agreed on the definition of functor (which I think we do), and all the subsidiary notions that are being discussed are recognised as being the development of something different, but possibly equivalent (in the non-technical sense), to what everyone recognises as being functors. A main strength of category theory is that it deconflates definitions and ideas so that we can be really precise. A lot of this has felt like going backwards, in that it has been assumed that the NewFunctors(TM) are the same as functors, whereas the theory should be worked out solidly first, and made precise, and then we can try to see if what we have is the same. That being said, there is room for interplay, but it should be kept in mind that if you (Eric) are after some handy computational notation, then please don't give it the same name as what it is representing. Even the defining representation of a matrix group is held to be distinct from the group itself. -
- CommentRowNumber53.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
Sure, David. I'll do my best to not use the standard term when I mean the "speculative yet hopefully equivalent" alternative. I'm sure I slipped a few times.
Did my response above make any sense? When we are dealing with sets
 and
and 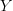 , we really do just form the cograph (I'm pretty sure) and
, we really do just form the cograph (I'm pretty sure) and 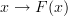 is a morphism in the resulting poset.
is a morphism in the resulting poset. -
- CommentRowNumber54.
- CommentAuthorDavidRoberts
- CommentTimeMar 23rd 2010
I would personally think of this as the Cech groupoid (internal to Set) for the function
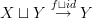 , and in that guise, it is very unintuitive in comparison to the definition of function, seeing as we already have to use the definition of function to define it. This is slightly reminiscent of the development of SEAR, in that relations are taken as fundamental, and functions derived from them. Are you implicitly defining a category with objects category and arrows discrete (op)fibrations (or something - the details are not important for your purposes for now), examples being cographs of functors in the ordinary sense, analogous to Rel, the category of sets and relations?
, and in that guise, it is very unintuitive in comparison to the definition of function, seeing as we already have to use the definition of function to define it. This is slightly reminiscent of the development of SEAR, in that relations are taken as fundamental, and functions derived from them. Are you implicitly defining a category with objects category and arrows discrete (op)fibrations (or something - the details are not important for your purposes for now), examples being cographs of functors in the ordinary sense, analogous to Rel, the category of sets and relations? -
- CommentRowNumber55.
- CommentAuthorUrs
- CommentTimeMar 23rd 2010
If we need to use the word "cograph", then let's if it helps :)
I'd really rather not.
Why not?
Because I am worried that we jump into sophisticated discussion before the plain basics have been straightened out.
I feel we already spent much time in similar discussions before with trying to guess sophisticated incarnations that might match your intuition. That is fun, too, but I am not sure if it really helps you understand what's going on. After all, the definition of category, functor and natural transformaiton is kindergarten stuff, and I don't tink it serves to obscure this continually.
For instance what you said last time about the adjunction
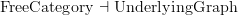 seemed to suffer from you insistence of not accepting the plain simple definition of functor.The adjunction
seemed to suffer from you insistence of not accepting the plain simple definition of functor.The adjunction 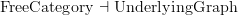 is also kindergarten-easy. Take a piece of paper and a pencil and 15 minutes of quietness and write out what this adjunction means. When you understand this, you will have understood what functors really are.
is also kindergarten-easy. Take a piece of paper and a pencil and 15 minutes of quietness and write out what this adjunction means. When you understand this, you will have understood what functors really are. -
- CommentRowNumber56.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
Hey wait a minute! [feigns indigination]
The discussion you are referring to is here. I won't say it is impossible that what I said "suffer[ed] from the insistence of not accepting the plain simple definition of functor", but I don't think that is the case. What I said certainly suffered from a lack of understanding of adjunctions for sure, but that was one of the main points of my line of questions, i.e. learning about adjunctions.
And to say that adjunctions are "kindergarten stuff" indicates that you have really lost touch with reality :)
Of course everything is "kindergarten easy" once you understand it, so us mortals actually have to suffer to learn things :P
Anyway, I'll try not to be too hurt by your comment [hmmpf!] :)
I still appreciate that
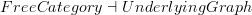 is a simple example and I intend to spend some time on it, but since I am mortal, I assure you it will be more than 15 minutes :)
is a simple example and I intend to spend some time on it, but since I am mortal, I assure you it will be more than 15 minutes :) -
- CommentRowNumber57.
- CommentAuthorUrs
- CommentTimeMar 23rd 2010
Sorry, Eric, but I am confused about what you are confused about. Back in that discussion I had the impression that you had a wrong idea about what the functors
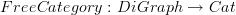 and the functor
and the functor 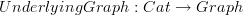 do. And it seemed to me that this was caused by an insistence of thinking about functors in a funny way.
do. And it seemed to me that this was caused by an insistence of thinking about functors in a funny way.I don't know, i am just trying to be of help and suggest that you concentrate on the simple facts first. You have to understand that I am a bit confused by the fact that we discuss the plain notion of functors for weeks. I might be misunderstanding what you are really thinking about, of course,
if you like, ignore the adjunction property for the time being. Let's just see if we can agree on what exactly the two functors
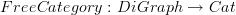 and
and 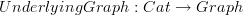 do.
do. -
- CommentRowNumber58.
- CommentAuthorUrs
- CommentTimeMar 23rd 2010
Maybe to recall, the statement in question was this one:
for
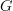 a directed graph and
a directed graph and 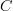 a category, a functor
a category, a functor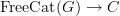
is "the same thing" as a morphism of graphs
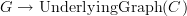 .
.I don't want to be posing exercises as any stupid math book. I am willing to explain this in lots of detail. But I am unsure which part is clear and where the non-clarity begins.
-
- CommentRowNumber59.
- CommentAuthorHarry Gindi
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
I e-mailed him exercises as well. This is in fact a problem from that packet (Show that Pa: Dia -> Cat is left adjoint to U: Cat -> Dia).
Where Pa denotes the path category i.e. the free category, and U denotes the forgetful functor.)
Dia is the category of Diagram schemes (i.e. quivers, i.e. oriented graphs).
-
- CommentRowNumber60.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
You wouldn't know it by the quantity of posts, but in the weeks we've been talking about this, if you sum up all the time I have been able to actually think about it, it probably adds up to about 30 minutes :)
I've always been a pretty hard worker, but the new life in HK is tough. I'm sitting down now after a very intense 14 hour day at work. This place being my only solace for distractions.
David mentioned something in that other thread about underlying graphs that illustrated an extra degree of confusion on my part. Given a category with 3 objects
 ,
, 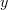 , and
, and  and three non-identity morphisms
and three non-identity morphisms 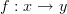 ,
, 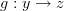 and
and 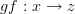 , what is its underlying graph? There are two options I can think of:
, what is its underlying graph? There are two options I can think of: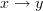 ,
, 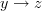 , and
, and  , or
, or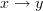 and
and 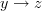
What David said (if I understood correctly, which is always a big "if") seemed to indicate the correct choice is 1.) , whereas I always thought it should be 2.). I always thought
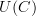 should be the "smallest" graph such that you can recover
should be the "smallest" graph such that you can recover  (or something "equivalent" in some way) when constructing the quiver
(or something "equivalent" in some way) when constructing the quiver 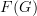 . I figured you wouldn't need the directed edge
. I figured you wouldn't need the directed edge  in
in 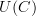 because this comes for free when you construct the quiver of the TWO directed edges
because this comes for free when you construct the quiver of the TWO directed edges 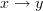 and
and 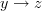 .
.Basically, two different directed graphs can have the same quiver, so which one should you take as the underlying one? The "full one" (including all composite edges) or the "smallest" one (containing only non-composite edges)?
I should probably try to clear that up before moving on. Which is it? Is
 in
in 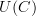 ?
?Thank you very much for all your help.
-
- CommentRowNumber61.
- CommentAuthorHarry Gindi
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
No, the underlying (read: forgetful) graph is just if you do the stupid thing and turn all of your objects into vertices and if you turn all of your morphims into directed paths.
Similarly, the free category is if you do the stupid thing again and just generate a catgory from a graph by composing by concatenation and letting the concatenation of no paths at an object be the identity.
This is also in those notes I sent you.
-
- CommentRowNumber62.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
Thanks Harry. Yeah, I am looking for the notes you gave me. My filing system is not great :o It should be here somewhere... Edit: Found it!
-
- CommentRowNumber63.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
I'm trying to fight the temptation of asking "why" the forgetful functor can't forget the maximum amount of information...
I will hold off on that one for another time and just accept that the forgetful functor is the "stupid" one for now.
PS: Thanks again for the notes Harry. These are good. When I started reading them the first time, I got scared pretty quickly. On second glance, I might have given up too easily.
-
- CommentRowNumber64.
- CommentAuthorHarry Gindi
- CommentTimeMar 23rd 2010
Remember that that functor is not a functor from some given category to a graph, but rather a functor from the 1-category of categories to graphs. It sends each category
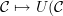 . Note the arrow that I've used here.
. Note the arrow that I've used here. -
- CommentRowNumber65.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
The devil on my left shoulder tells me to ask. The angel on my right shoulder tells me to forget it. Unfortunately, the devil almost always wins.
Let me denote
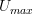 to be a map (I won't call it a functor, because the answer to my question may lay in the fact that
to be a map (I won't call it a functor, because the answer to my question may lay in the fact that 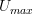 may not be a functor)
may not be a functor)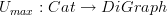
that given a category
 produces the smallest directed graph such that
produces the smallest directed graph such that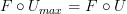
where
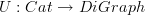 is the usual forgetful functor.
is the usual forgetful functor.Is
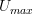 a functor?
a functor?Edit: Light bulb. I'm going to go out on a limb and assume
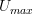 is a functor, but note that
is a functor, but note that 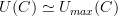 for any category
for any category  because there is an isomorphism between the "smallest" and the "fullest" graphs. For example, starting with the "fullest" graph, we can forget all composites to get the "smallest" graph. We can exactly recover the "fullest" graph from the "smallest" graph by inserting all composites.
because there is an isomorphism between the "smallest" and the "fullest" graphs. For example, starting with the "fullest" graph, we can forget all composites to get the "smallest" graph. We can exactly recover the "fullest" graph from the "smallest" graph by inserting all composites.Edit^2: Now that that is cleared up, I really can move on. Yay!
-
- CommentRowNumber66.
- CommentAuthorHarry Gindi
- CommentTimeMar 23rd 2010
Functors must preserve morphisms and commute with composition. You have not shown this, therefore all that you've done is map a category to a graph. This is not valid, and it means that you are still misunderstanding the notion of a functor.
-
- CommentRowNumber67.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
@Harry: In these notes, what he calls
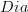 is the same as what we call
is the same as what we call 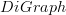 . However, a diagram scheme (or directed graph)
. However, a diagram scheme (or directed graph) 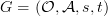 does not necessarily include all composite edges. For example, if
does not necessarily include all composite edges. For example, if 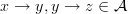 , then it is not necessary that
, then it is not necessary that  is in
is in 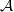 . Therefore, generally speaking,
. Therefore, generally speaking, 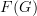 is not necessarily a category as described. To make sure that
is not necessarily a category as described. To make sure that 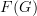 is a category, we need to associate a morphism to each
is a category, we need to associate a morphism to each 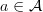 and then ALSO add morphisms to fill in the missing composites. Unless I'm overlooking something, this last step appears to be missing from the notes.
and then ALSO add morphisms to fill in the missing composites. Unless I'm overlooking something, this last step appears to be missing from the notes.Edit: I didn't see your comment above before writing this, so responded below.
-
- CommentRowNumber68.
- CommentAuthorIan_Durham
- CommentTimeMar 23rd 2010
I'm following this conversation as an interested observer and someone who is in Eric's shoes (actually well-behind Eric in my knowledge level). I just wanted to say to Eric: I can empathize with your work schedule. Mine is similar. :) -
- CommentRowNumber69.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
Functors must preserve morphisms and commute with composition. You have not shown this, therefore all that you've done is map a category to a graph. This is not valid, and it means that you are still misunderstanding the notion of a functor.
@Harry: I have shown that for any category
 that
that 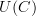 and
and 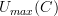 are isomorphic. I believe this is enough to conclude that
are isomorphic. I believe this is enough to conclude that 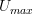 is indeed a functor. It is kind of cool.
is indeed a functor. It is kind of cool. -
- CommentRowNumber70.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
- (edited Mar 24th 2010)
I specialize in hand waving, but here is my best attempt at an actual proof...
The objects of
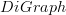 can be partitioned into three disjoint sets:
can be partitioned into three disjoint sets:[Edit: This partition is not 100% correct as stated. It needs some work, but the basic idea should remain. This issue is pointed out In a comment below from David. We need to take care of digraphs having non-trivial loops, but that can be sorted out, so in what follows, consider it to be restricted to "digraphs without non-trivial loops".]
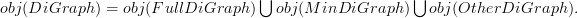
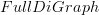 is a full subcategory of
is a full subcategory of 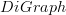 consisting of those digraphs for which all composite edges are included, i.e. if
consisting of those digraphs for which all composite edges are included, i.e. if 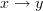 and
and 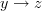 are directed edges, then
are directed edges, then  is also a directed edge.
is also a directed edge.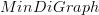 is a full subcategory of
is a full subcategory of 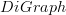 consisting of those digraphs that contain no composite edges, i.e. if
consisting of those digraphs that contain no composite edges, i.e. if 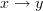 and
and 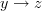 are directed edges, then
are directed edges, then  is NOT a directed edge.
is NOT a directed edge.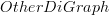 is a full subcategory of
is a full subcategory of 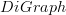 consisting of all other digraphs, i.e. the ones that are neither full or minimal.
consisting of all other digraphs, i.e. the ones that are neither full or minimal.Given any full digraph, we can obtain a minimal digraph by removing all composite edges. Conversely, given any minimal digraph, we can obtain a full digraph by adding all composite edges. This process is reversible.
Let
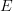 be an endofunctor on
be an endofunctor on 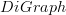 defned by (evil alert!)
defned by (evil alert!)- For any
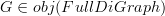 ,
, 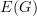 is the corresponding minimal digraph
is the corresponding minimal digraph - For any
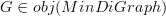 ,
, 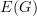 is the corresponding full digraph
is the corresponding full digraph - For any
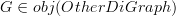 ,
, 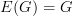
and it does the obvious thing to morphisms.
A neat thing about this is the endofunctor squares to an identity functor and we have
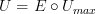
and
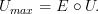
From here, it is obvious (even to me) that
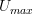 is a functor since both
is a functor since both 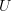 and
and 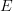 are functors.
are functors. -
- CommentRowNumber71.
- CommentAuthorEric
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
The above calculation also answered my follow up question, 'What is the left adjoint of
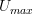 ?"
?"SInce
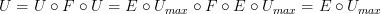
we can apply
 to the left to get
to the left to get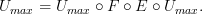
Similarly,
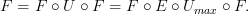
Pre-composing
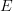 on the right, we get
on the right, we get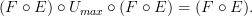
If I'm not mistaken, the above two facts imply that
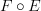 is the left adjoint of
is the left adjoint of 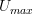 .
. -
- CommentRowNumber72.
- CommentAuthorHarry Gindi
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
You never addressed my comment about morphisms. Are you familiar with what the morphisms are in the 1-category of small 1-categories are?
To be clear, you need to show that the "functor" you're defining commutes with composition of functors and sends identities to identities as well. In this case, Hom(C,D) is the set of functors between C and D.
Basically your definitions are broken and don't make any sense.
The way that the standard definition of this forgetful functor actually works is as follows:
For any category C in (1-Cat of small 1-Cats)
Let C_0=Ob(C) is a set of points. For every element of Hom(X,Y), give an edge from the point X to the point Y.
This pair U(C):=(C_0, C_1) defines a quiver.
Then to show that this is functorial: Given a functor C->D, U(C->D) gives a morphism of graphs because functors send objects to objects and hom sets to hom sets, so applying the construction, this gives us a well-defined map of quivers.
U(Id_C) is obviously the map that we want, since it is the identity on points and edges.
U(G o F) commutes with composition again for the obvious reason (functors map objects to objects and arrows to arrows, so this gives us morphisms of graphs that do the same thing).
Do you see what I've just done? I've described the behavior of morphisms (functors in this case) under the action of the functor.
You're being willfully ignorant here. The definition of a functor is a good one (modulo strictness and constructibility concerns, which are irrelevant.)
-
- CommentRowNumber73.
- CommentAuthorUrs
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
I'm trying to fight the temptation of asking "why" the forgetful functor can't forget the maximum amount of information...
A category is a directed graph with the extra information of how to compose morphisms. Therefore we want to speak of the forgetful functor that forgets precisely this extra information.
but note that
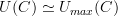
as far as I understand what you wrote, in fact
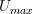 is the same as
is the same as  .
.What Harry says above is correct. For
 a category with set of objects
a category with set of objects 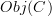 and set of morphisms
and set of morphisms 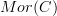 and maps
and maps 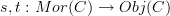 that send each morphisms to its source and target object, and with some composition operation, the underlying directed graph
that send each morphisms to its source and target object, and with some composition operation, the underlying directed graph 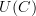 is precisely this data, but forgetting that there is a composition operation.
is precisely this data, but forgetting that there is a composition operation.So the set of vertices of
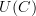 is the set
is the set 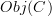 and the set of edges of
and the set of edges of 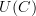 is
is 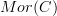 and the maps that send each edge to its source and target are
and the maps that send each edge to its source and target are  and
and 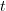 , respectievly.
, respectievly.For
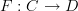 a functor between categories, which is given by some maps of objects
a functor between categories, which is given by some maps of objects 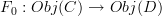 and some maps of morphisms
and some maps of morphisms 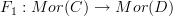 the value of the functor
the value of the functor 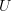 on
on 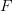 is the morphism of graphs
is the morphism of graphs 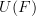 that has precisely the same action, now regarded as a map between sets of vertices and edges of graphs.
that has precisely the same action, now regarded as a map between sets of vertices and edges of graphs.One can see easily that for
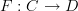 and
and 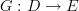 two functors, i.e. two morphisms in the category of categories, we have the relation
two functors, i.e. two morphisms in the category of categories, we have the relation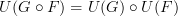
between morphisms of directed graphs. So
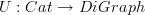 is indeed a functor.
is indeed a functor.Okay?
-
- CommentRowNumber74.
- CommentAuthorDavidRoberts
- CommentTimeMar 24th 2010
Eric,
in trying to construct some 'minimal quiver' of which a category is a path category on, you will, run into trouble. Given a groupoid with 3 objects a,b,c, all of which are uniquely isomorphic (so we have arrows a -> b, b -> c, a -> c, b -> a, c -> b, c -> a plus identity arrows, such that what we have here are inverses of each other) how do we pick, *in a systematic way* (or natural way) the arrows which supposedly form this minimal quiver? And so on for all other finite groupoids, all other finite categories and so on to all small categories.
If you have a (deloopong of a) monoid, i.e. a category with one object, then sending it to the underlying graph forgets two things: which arrows are composites of other arrows, and which arrow was the identity. So the underlying graph functor cannot remember the identity arrow to throw it out. So when above you said
>What David said (if I understood correctly, which is always a big "if") seemed to indicate the correct choice is 1.) , whereas I always thought it should be 2.)
actually it's neither, as you need to include the identity arrows as well (recall I said there should be six edges in the underlying directed graph of your category.
You do need to be careful about making statements like 'such and such is a functor from Cat to DiGrph', based on the consideration of a single specialised example at the extreme end of a spectrum. Other extreme examples, like the monoid above, or the groupoid need to be considered. It's all very well and good considering something that we know to be the free category on a finite directed graph (of a simple sort) and, by hand and outside the rules of the game, reconstructing the graph. But not all categories are of this form, and not even categories of this form plus some conditions (c.f. the monoid above).
Using the axiom of choice you can construct a map Ob(Cat) -> Ob(DiGrph) of the sort you describe, but you *cannot* make all the choices and still respect the algebraic structure (i.e. the arrows) of Cat and DiGrph. This latter point is the most important. Categories are algebraic structures, and you need all constructions to work with the maps between them. -
- CommentRowNumber75.
- CommentAuthorEric
- CommentTimeMar 24th 2010
- (edited Mar 24th 2010)
Too bad! I actually spent a lot of time thinking last night to demonstrate that I'm trying (even though I was exhausted). I lost a lot of sleep because of it. I was very happy with what I came up with, so I am kind of sad that there was no "Good job" or "That is interesting". All I got was "You're being willfully ignorant here."
Harry answered my question about what the underlying graph
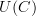 should be. There were two options, he told me the correct one. I accepted it happily. His answer agreed with what David said and is double confirmed by Urs. The "correct" forgetful functor is the one that keeps all composite edges. Fine.
should be. There were two options, he told me the correct one. I accepted it happily. His answer agreed with what David said and is double confirmed by Urs. The "correct" forgetful functor is the one that keeps all composite edges. Fine.THIS IS A FUNCTOR. OBVIOUSLY! I never said it was not a functor. Ever.
I had a different functor in mind, but that is fine as long as I understand everything.
as far as I understand what you wrote, in fact
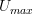 is the same as
is the same as 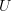 .
.Argh. No. Here is a concrete example. Given a category
 with three objects
with three objects 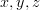 and 3 non-identity morphism
and 3 non-identity morphism 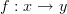 ,
, 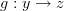 , and
, and 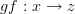 (as above)
(as above)[Note: I'll address David's super helpful (as always) comments about groupoids a little later.]
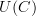 is the directed graph consisting of three nodes and THREE (non self-looping) edges corresponding to the non-identity morphisms and three self-loops corresponding to the identities (per David's comment above).
is the directed graph consisting of three nodes and THREE (non self-looping) edges corresponding to the non-identity morphisms and three self-loops corresponding to the identities (per David's comment above).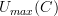 is the directed graph consisting of three nodes and only TWO (non self-looping) edges corresponding to the non-composite non-identity edges. It does not contain an edge corresponding to the morphism
is the directed graph consisting of three nodes and only TWO (non self-looping) edges corresponding to the non-composite non-identity edges. It does not contain an edge corresponding to the morphism 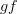 .
.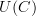 has three (non self-looping) edges.
has three (non self-looping) edges. 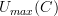 has two (non self-looping) edges. How can they be the same????
has two (non self-looping) edges. How can they be the same????I then proceeded to construct a[n] (what I thought was a very neat) endofunctor on
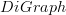 . I used the fact the
. I used the fact the 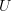 was a functor and
was a functor and 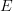 was a functor to prove that
was a functor to prove that 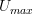 is also a functor. I didn't follow Harry's suggestion and prove it was a functor by showing it preserves compositions and identities, but so what? If
is also a functor. I didn't follow Harry's suggestion and prove it was a functor by showing it preserves compositions and identities, but so what? If 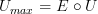 and both
and both 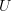 and
and 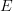 are functors, then
are functors, then 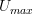 is obviously a functor.
is obviously a functor.Of course
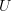 is a functor. I would not say otherwise or I'd be accusing everyone here AND MacLane AND Pratt and Harry's professor of being wrong. That would be "willfully ignorant". But I never did that.
is a functor. I would not say otherwise or I'd be accusing everyone here AND MacLane AND Pratt and Harry's professor of being wrong. That would be "willfully ignorant". But I never did that.I had a misunderstanding of what
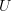 was. That misunderstanding was cleared up. I defined a new forgetful functor
was. That misunderstanding was cleared up. I defined a new forgetful functor 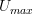 , but that doesn't imply anything about
, but that doesn't imply anything about 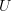 .
.Later, I even used the fact that
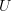 was a functor AND even that
was a functor AND even that 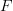 is its adjoint functor to construct an adjoint to
is its adjoint functor to construct an adjoint to 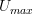 .
.Now if by
as far as I understand what you wrote, in fact
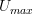 is the same as
is the same as 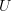 .
.you meant "equivalent", then that is true in the sense that there is an isomorphism
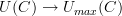 for any category
for any category  , but even though two directed graphs, each having different number of edges, can be mapped to each other in a reversible matter, I'd still (from a graph theory perspective) consider them different objects if they had different numbers of edges.
, but even though two directed graphs, each having different number of edges, can be mapped to each other in a reversible matter, I'd still (from a graph theory perspective) consider them different objects if they had different numbers of edges.Regarding David's comment...
Good point! Thank you :)
You are right. For
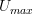 to be defined unambiguously, its domain must be restricted to somehow "causal" categories. Maybe generalized direct category or generalized Reedy category or something. Basically, to categories without non-trivial loops. This excludes groupoids as you pointed out.
to be defined unambiguously, its domain must be restricted to somehow "causal" categories. Maybe generalized direct category or generalized Reedy category or something. Basically, to categories without non-trivial loops. This excludes groupoids as you pointed out.But this is not as bad as it sounds at first. As I was trying to describe recently, a groupoid can always be "extruded" to a "causal" category (yet to be defined, but is probably one of the two: direct or Reedy).
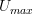 is unambiguously defined on "categories with direction" and I hope to prove some day that any category can be extruded to a category with direction. At the moment, most terms in that statement are yet to be defined. It is one of my homework assignments.
is unambiguously defined on "categories with direction" and I hope to prove some day that any category can be extruded to a category with direction. At the moment, most terms in that statement are yet to be defined. It is one of my homework assignments.So my conclusion from this is that
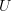 is the right functor.
is the right functor. 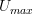 may or may not be interesting, so we can forget about it. Most important, I have learned something.
may or may not be interesting, so we can forget about it. Most important, I have learned something.Note to Urs: Please please know that I understand
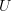 is a functor. I even know it is the RIGHT functor. I knew that when I wrote my comment above last night, so please, with that in mind, have another look at what I wrote. I do think it is interesting.
is a functor. I even know it is the RIGHT functor. I knew that when I wrote my comment above last night, so please, with that in mind, have another look at what I wrote. I do think it is interesting. -
- CommentRowNumber76.
- CommentAuthorHarry Gindi
- CommentTimeMar 24th 2010
The reason that I provided a proof was to give you an example of what a proof of functoriality entails. Then Urs posted his version of the proof because my version wasn't very clear.
Still, you're missing the point. This case is very confusing because you're talking about the functor U, and the "functors", i.e. the 1-cells in the 1-category of small 1-categories. The problem with what you're doing is that you're trying to give a morphism between a category and a graph, which is strictly not something that can be done. What you have to prove is precisely that your functor U_max commutes with composition and sends identities to identities. The internal structure other category has remarkably little to do with the actual problem.
-
- CommentRowNumber77.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
- (edited Mar 24th 2010)
Eric,
you defined
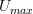 as follows:
as follows:Let me denote
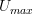 to be a map (I won't call it a functor, because the answer to my question may lay in the fact that U_{max} may not be a functor)
to be a map (I won't call it a functor, because the answer to my question may lay in the fact that U_{max} may not be a functor)
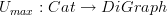 that given a category
that given a category  produces the smallest directed graph such that
produces the smallest directed graph such that 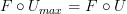 .
.I think this definition makes them the same. The free category functor is injective on objects: if two graphs are different, then their free categories are different.
The two concrete examples of graphs you call
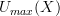 and
and 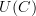 in your latest comment are not equal. But they are also not isomorphic.
in your latest comment are not equal. But they are also not isomorphic.I am not sure what
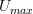 is needed for!
is needed for!Another thing: above you write
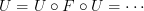
Here
 is still the free category functor? Then
is still the free category functor? Then  is the graph whose edges are words in the morphisms of
is the graph whose edges are words in the morphisms of  . But
. But 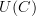 is the graph whose edges are just the morphisms in
is the graph whose edges are just the morphisms in  . The former is much bigger.
. The former is much bigger. -
- CommentRowNumber78.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
Note to Urs: Please please know that I understand U is a functor. I even know it is the RIGHT functor. I knew that when I wrote my comment above last night, so please, with that in mind, have another look at what I wrote. I do think it is interesting.
I am looking. But now where are we? So we understand the functor
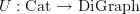 now. What we are after is understanding that for
now. What we are after is understanding that for 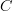 any category and
any category and 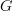 any graph, functors
any graph, functors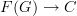
are in bijection with graph morphisms
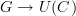 .
.Do you see how this works?
-
- CommentRowNumber79.
- CommentAuthorEric
- CommentTimeMar 24th 2010
Thanks Urs and sorry for the detour. I was confused about
 . Now I'm not. I'll do some work offline to iron out what I mean by
. Now I'm not. I'll do some work offline to iron out what I mean by  , but that is not important for the current exercise you've re-focused things on. I'm headed for a train now (and another intense day), so attention will be sporadic for a while...
, but that is not important for the current exercise you've re-focused things on. I'm headed for a train now (and another intense day), so attention will be sporadic for a while... -
- CommentRowNumber80.
- CommentAuthorHarry Gindi
- CommentTimeMar 24th 2010
The best you are going to get with
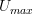 is
is 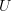 , and at worst, you won't get a functor at all.
, and at worst, you won't get a functor at all. -
- CommentRowNumber81.
- CommentAuthorEric
- CommentTimeMar 24th 2010
- (edited Mar 24th 2010)
In the other thread, you phrased the question in a nice digestible way (for me):
given a functor
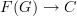 , which graph morphism
, which graph morphism 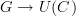 do you send it to? And how do you go the other way round?
do you send it to? And how do you go the other way round?The graph morphism we send
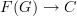 to would be
to would be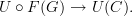
To go back the other way, the obvious thing to try would be
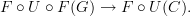
Although I mistakenly wrote
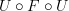 equals (which it doesn't)
equals (which it doesn't) 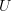 above, the other expression was correct, i.e. it is true that
above, the other expression was correct, i.e. it is true that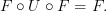
Therefore, going back the other way, we have a morphism
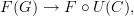
which is not exactly what we started with, but close.
So to finish the exercise, we need to demonstrate an isomorphism
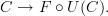
It seems obvious, i.e. there are corresponding objects and morphisms, but my time has expired for the moment...
-
- CommentRowNumber82.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
- (edited Mar 24th 2010)
we need to demonstrate an isomorphism
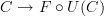 .
.This can't exist. There is a canonical functor the other way round:
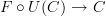 . But it is not an isomorphism (and not an equivalence) in general:
. But it is not an isomorphism (and not an equivalence) in general:the category
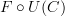 is the category whose objects are those of
is the category whose objects are those of  , and whose morphisms are words of composable morphisms in
, and whose morphisms are words of composable morphisms in 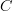 . Composition in
. Composition in 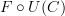 is just concatenation of such words.
is just concatenation of such words.Now, every such word in composable morphisms can be evaluated to one single morphism in
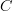 : we we just take all the morphisms in the word and form their composite using the composition rule provided with
: we we just take all the morphisms in the word and form their composite using the composition rule provided with 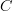 . This assignment
. This assignment 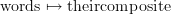 is easily seen to be a functor from
is easily seen to be a functor from 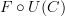 to
to  . This functor is called the counit of the adjunction . Of the adjunction that we are wanting to establish.
. This functor is called the counit of the adjunction . Of the adjunction that we are wanting to establish.To get that, we should try to explitly say what it is that a functor
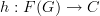 does. Say out in words which data you have to specify in order to describe such a functor
does. Say out in words which data you have to specify in order to describe such a functor 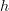 to me.
to me.Here is a hint: the functor
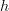 needs to send every morphism in
needs to send every morphism in 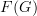 to a morphism in
to a morphism in 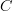 , such that this respects composition. The morphisms in
, such that this respects composition. The morphisms in 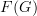 are words of consecutive edges in the graph
are words of consecutive edges in the graph 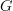 . Their composition operation is just the concatenation of words.
. Their composition operation is just the concatenation of words.So in particular there are the words of length 1, and the functor
 needs to send each of them to some morphism in
needs to send each of them to some morphism in  . Suppose this assignment of a morphism in
. Suppose this assignment of a morphism in  for each morphism in
for each morphism in 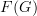 that is a word of length 1 is given. What other information is there needed in order to specify a functor
that is a word of length 1 is given. What other information is there needed in order to specify a functor 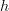 , i.e. in order to specify what it does to words of legnth greater than 1 ? Is there any further information needed? Can we use the functoriality of
, i.e. in order to specify what it does to words of legnth greater than 1 ? Is there any further information needed? Can we use the functoriality of 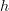 (the fact that it respects composition) in order to deduce what it does to words of length greater than 1?
(the fact that it respects composition) in order to deduce what it does to words of length greater than 1?The answer is yes. Do you see how this works?
So from this reasoning we find that specifying a functor
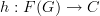 is the same thing as giving a map of sets
is the same thing as giving a map of sets 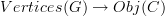 and a map of sets
and a map of sets 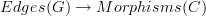 that matches the previous assignment on source and target objects. And nothing else. By functoriality of
that matches the previous assignment on source and target objects. And nothing else. By functoriality of  alone it follows that this fixes what
alone it follows that this fixes what  does on all morphisms of
does on all morphisms of 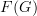 .
.But what we just specified is manifestly nothing but a map of graphs
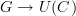 .
.So functors
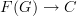 encode precisely the same informaton as morphisms of graphs
encode precisely the same informaton as morphisms of graphs 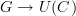 .
.This is the adjunction isomorphism. We may write it as a bijecton of sets
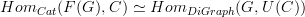 .
.Do you see what I mean?
(In fact to establish an adjunction we also need to check that this bijection is "natural". But let's not worry about that for the time being.)
1 to 82 of 82