nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorHarry Gindi
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
Would anyone be opposed to giving the definition of pointwise Kan extension as a Kan extension that is preserved by all co-representable functors (i.e.
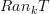 is a pointwise kan extension if
is a pointwise kan extension if 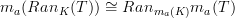 where
where 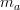 denotes the functor
denotes the functor 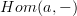 .
.I looked this up in Mac Lane's Categories Work, but I'm not sure that I interpreted "preserved by
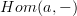 for all objects a" correctly.
for all objects a" correctly.Mac Lane also makes the point of assuming that the category has small Hom-sets, but I think that distinction is unnecessary unless we're being cardinality-strict for no reason.
-
- CommentRowNumber2.
- CommentAuthorMike Shulman
- CommentTimeMar 23rd 2010
Of course not. Mac Lane's assumption of local smallness is just because a category that is not locally small has no hom-functors landing in Set, so the definition is meaningless. Not everyone believes that proper classes are just sets of some bigger universe in disguise.
-
- CommentRowNumber3.
- CommentAuthorHarry Gindi
- CommentTimeMar 23rd 2010
I don't see the use of assuming otherwise. Is there a good argument for having hom sets that are actually proper classes? I mean, on questions that are independent of set theory, shouldn't we take the answer that allows us to do the most?
-
- CommentRowNumber4.
- CommentAuthorDavidRoberts
- CommentTimeMar 23rd 2010
Given Set (not U-Set, but some non-strict category of all sets, say), then the category of presheaves with values in Set has whopping big hom-sets, if I remember rightly -
- CommentRowNumber5.
- CommentAuthorHarry Gindi
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
We can systematically excise every occurrence of Set in any mathematical document by replacing Set with U-Set and making the necessary changes to be relative to U.
This gives us the Yoneda embedding for any category, which is no trivial matter.
-
- CommentRowNumber6.
- CommentAuthorDavidRoberts
- CommentTimeMar 23rd 2010
But we might not want to assume the axiom of universes...
-
- CommentRowNumber7.
- CommentAuthorHarry Gindi
- CommentTimeMar 23rd 2010
To what end?
-
- CommentRowNumber8.
- CommentAuthorDavidRoberts
- CommentTimeMar 23rd 2010
centipede mathematics, perhaps. People around here, I've noticed, tend to try and do this sort of thing. You might as well ask, why do without the axiom of associativity? The answer is, of course, why not? If things break, we want to know precisely why and how.
1 to 8 of 8