nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorMike Shulman
- CommentTimeJan 6th 2010
How would people feel about renaming distributor to profunctor? I seem to recall that when this came up on the Cafe, I was the main proponent of the former over the latter, and I've since changed my mind.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeJan 6th 2010
sure, fine with me
-
- CommentRowNumber3.
- CommentAuthorTodd_Trimble
- CommentTimeJan 6th 2010
I rather prefer profunctor to distributor, and I have a slight preference for bimodule over profunctor.
-
- CommentRowNumber4.
- CommentAuthorTobyBartels
- CommentTimeJan 6th 2010
I'm moderately in favour of the proposed move.
-
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeJan 9th 2010
I made the change moving distributor to profunctor. If you want, Todd, we could discuss whether to use bimodule instead, but I think that term is too confusing for most mathematicians, and/or not specific enough.
-
- CommentRowNumber6.
- CommentAuthorEric
- CommentTimeJan 10th 2010
I think I know a little bit about bimodules (not much) and I know I don't know anything about profunctors (I even struggle with functors). I remember when Urs had his first Eureka moment about bimodules. I wish I could reproduce that feeling. Is there a way to understand it for someone who thinks of bimodules as "kind of like vectors"? In what way is a profunctor "kind of like a vector space"?
When I look at profunctor, it is completely intimidating and I do not understand a word.
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeJan 10th 2010
- (edited Jan 10th 2010)
Eric,
the basic kind of module that you are familiar with is a vector space: an additive group (vectors and their addition) on which you can act with a number field, say with the real numbers.
A bimodule is like a vector space, only that there are two possibly different actions of the real numbers on it. A way to multiply a vector by a number from the left -- or from the right.
Every vector space is hence also a bimodule over the ground field, where we take the left and the right multiplication by a number on a vector to be the same.
You know the tensor product of vector spaces. That's "tensoring over the field" that acts on them. If we think of vector spaces as bimodules over te ground field (multiplication by real numbers on vectors from left and right) then the tensor product of
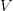 with
with 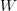 is to be thought of cancelling the right action on V with the left action on W, leaving
is to be thought of cancelling the right action on V with the left action on W, leaving 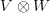 with the left action on V remaining and the right action on W.
with the left action on V remaining and the right action on W.In this way tensoring with W gives an assignment
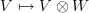 .
.This perspective generalizes. There is a way to replace in the above picture vector spaces regarded as one-sided modules with presheaves (one-sided modules) and vector spaces regarded as bimodules with profunctors (= 2-sided modules).
-
- CommentRowNumber8.
- CommentAuthorEric
- CommentTimeJan 10th 2010
.. and don't forget my favorite example of bimodules, i.e. discrete differential forms :)
The key is the last paragraph of course. I'll have to try to understand that. Thanks!
-
- CommentRowNumber9.
- CommentAuthorzskoda
- CommentTimeJan 10th 2010
Profunctoris far more suggestive than distributor for outsiders, which does not even remind of functor...
-
- CommentRowNumber10.
- CommentAuthorTobyBartels
- CommentTimeJan 10th 2010
The term ‘bimodule’ is so general, encompassing the case that Urs describes in #7 above as well, that I would want to keep bimodule what it is, and make profunctor (or distributor, but we've already discussed that) the page that focusses on the case at hand.
-
- CommentRowNumber11.
- CommentAuthorTodd_Trimble
- CommentTimeJan 12th 2010
Okay, that's fine. Profunctor it is, then, for this case.
-
- CommentRowNumber12.
- CommentAuthorMike Shulman
- CommentTimeApr 2nd 2010
I did some reorganizing of profunctor, and also added the two ways to describe them as fibrations or cofibrations.
@Toby #10, bimodule is currently actually about profunctors. I would prefer that bimodule be more general, as you seem to be suggesting, since for many/most mathematicians it is used restricted to the one-object case; with anything there that is specifically about profunctors moved to profunctor. In any case, bimodule should not duplicate profunctor, so if we decide that bimodule should be mostly about profunctors, then I think it should instead just redirect to profunctor.
-
- CommentRowNumber13.
- CommentAuthorTim_Porter
- CommentTimeApr 3rd 2010
Given recent remarks on the cat list, perhaps a separate entry on distributors with references to Benabou's work would be a good thing to include, of course, with a clear link to the profunctor page.
-
- CommentRowNumber14.
- CommentAuthorMike Shulman
- CommentTimeApr 3rd 2010
In general, I disagree with the idea of having multiple pages about the same thing, regardless of how many names that thing might have. I think it's better to pick a particular name, explain up-front that there are others in use, and use redirects. Of course, adding any additional references to Benabou's work on the profunctor page would be a great idea.
-
- CommentRowNumber15.
- CommentAuthorHurkyl
- CommentTimeOct 1st 2018
I know that I’m rather late to the party, but the name “profunctor” seems to conflict with the choice of convention that Prof(C,D) to be a functor D^op x C -> Set.
I understand that the motivation for the convention is based on the idea of generalizing the codomain of a functor to be the colimit-completion: i.e. a functor C -> PSh(D). But from the prefix “pro” I would have expected instead generalizing to the limit-completion, and thus to the alternate convention C^op x D -> Set. The given convention might be better named “indfunctor”.
Is the given choices just that profunctor is everyone’s favorite name and the colimit completion is everyone’s favorite concept, and so the two are paired? Or is there some other motivation that I’m missing?
-
- CommentRowNumber16.
- CommentAuthorTodd_Trimble
- CommentTimeOct 1st 2018
The naming conflict with the ’pro-’ as in ’profinite’ is well-known. ’Profunctor’ is not “everyone’s favorite name”, but the problem is that the name is ancient and entrenched, and we have no plans to change it. (I’m pretty sure we discussed this in another thread.) I don’t know of any case where the conflict led to real confusion.
-
- CommentRowNumber17.
- CommentAuthorMike Shulman
- CommentTimeOct 1st 2018
None of the existing terms for these objects — profunctor, distributor, (bi)module — is ideal. If we could (1) find a term that is completely unproblematic and (2) instantly convince all mathematicians to start using it, and retroactively edit all mathematical papers from the past to use it as well, then I think that would be a good thing. But in practice, even if we could do (1) (note that “ind-functor” is not perfect either, as it has the problem of suggesting a cocompletion under directed colimits only), what would actually happen is that instead of 3 competing terms there would be 4 competing terms, and even more confusion would be produced. As Jaap van Oosten said, “the only thing worse than bad terminology is continually changing terminology”. If a particular terminology is really bad, and nearly everyone agrees that it is bad and can be convinced to switch to the same alternative, then it is sometimes worth trying to change an established term (e.g. triple monad); but that case is extremely rare. As Todd says, this particular conflict rarely if ever leads to any actual confusion.
-
- CommentRowNumber18.
- CommentAuthortimhosgood
- CommentTimeJul 14th 2019
-
- CommentRowNumber19.
- CommentAuthorRichard Williamson
- CommentTimeJul 15th 2019
[Administrative note: I have merged an old thread, comments #1-#17, into this one. There is also this old thread, but I’ll not merge that one, since it covers both anafunctors and profunctors, and could fit into either latest changes thread.]
-
- CommentRowNumber20.
- CommentAuthorRichard Williamson
- CommentTimeJul 15th 2019
-
- CommentRowNumber21.
- CommentAuthorMike Shulman
- CommentTimeJul 17th 2019
I don’t quite understand what the paragraph is saying, but it doesn’t look right to me. Firstly, the profunctors having right adjoints are actually the ones that appear in the Cauchy completion; if the codomain is not Cauchy complete then they may not all be representable. Secondly, not all profunctors are Mealy morphisms either; I forget exactly what the characterization is in profunctorial terms but it’s not all of them (otherwise the term “Mealy morphism” wouldn’t have been introduced).
-
- CommentRowNumber22.
- CommentAuthorRichard Williamson
- CommentTimeJul 17th 2019
- (edited Jul 17th 2019)
(In case it is not clear, Mike in #21 is replying to #18). In case it helps, Mike’s first point more directly is I think that it is not necessarily true in the non-Cauchy complete case that profunctors corresponding to functors are exactly those with a right adjoint. It would be nice with an explicit counterexample!
MIke’s second point is I think that the correct statement is that Mealy morphisms determine profunctors, and that a profunctor can be obtained in this way if and only if it is ’discrete valued’. It comes from a functor if and only if it is total and discrete valued. See these slides of Paré. Thus we have ’inclusions’
Functors -> Mealy morphisms -> Profunctors
where the difference between Functors and Mealy morphisms is totality, and the difference between Mealy morphisms and Profunctors is discrete valuedness. In the Cauchy complete case, totality and discrete valuedness must be equivalent to having a right adjoint.
It would be great to improve the nLab entries on this, and in particular as I say with explicit counterexamples to show that the inclusions are strict, etc. I am no expert, but hopefully somebody else can do it. Great that you have begun on this, Tim!
-
- CommentRowNumber23.
- CommentAuthorMike Shulman
- CommentTimeAug 13th 2019
-
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeOct 15th 2021
Moving this old discussion from out of the entry to here:
begin forwarded discussion
+–{.query} Todd: There is an inevitable debate here about whether one should use or . My own convention is to use the latter. For example, every functor yields a profunctor by composition with the Yoneda embedding on .
Mike: My convention is . I agree with your reasoning for why should be contravariant; I like to put it first because in the hom-functor the contravariant variable appears first.
Sridhar Ramesh: But surely, just as well, a functor from to yields a contravariant functor from to and thus a profunctor , by composition with the contravariant Yoneda embedding of into ? At the moment, I still do not see why there is reason to prefer in the abstract general one to the other of and , though it’s not an issue I’ve thought very much about or have strong emotions regarding. Are there further reasons beyond the above?
Mike Shulman: Well, the covariant Yoneda embedding is arguably more natural and important than the contravariant one. If a profunctor ⇸ is a functor , then we can think of it as assigning to every a presheaf on , which may or may not be representable. The profunctor “is” a functor just when all its values are representable presheaves. Of course, if instead a profunctor ⇸ were a functor , i.e. , then we could think of it as assigning to each a functor , which might or might not be (co)representable. However, for a bunch of reasons it’s often more natural to think of an object of as determined by the maps into it, rather than the maps out of it—in other words by its generalized elements, or in yet other words by the presheaf it represents. Although of course formally, there is a complete duality. =–
end forwarded discussion
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeOct 15th 2021
- (edited Oct 15th 2021)
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeOct 21st 2021
- (edited Oct 21st 2021)
added pointer to:
- Maren Justesen, Bikategorien af Profunktorer, Aarhus 1968 (pdf)
(via user varkor, here)
Interesting: the entry used to claim that the original reference is Bénabou 1973 – only to list a couple more references from the 1960s.
I have now put the early references into chronological order.
Also I removed the claim that “the theory has mainly been developed by Bénabou”. If this needs to be said, let’s add it back in with some substantiation (e.g. saying what it is that Bénabou 1973 proves which other authors missed).
Also removed the claim that Bénabou 2000 is “excellent”. If this needs to be said, let’s add it back in with explanation of what is more excellent here than elsewhere.
-
- CommentRowNumber27.
- CommentAuthorSam Staton
- CommentTimeMay 4th 2022
-
- CommentRowNumber28.
- CommentAuthormaxsnew
- CommentTimeMay 17th 2022
-
- CommentRowNumber29.
- CommentAuthorvarkor
- CommentTimeSep 6th 2022
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeOct 4th 2022
added pdf link to
- Jean Bénabou, Les distributeurs, Université Catholique de Louvain, Institut de Mathématique Pure et Appliquée, rapport 33 (1973) [pdf]
-
- CommentRowNumber31.
- CommentAuthorJohn Baez
- CommentTimeApr 21st 2023
Changed
In general, right adjoint profunctors correspond to profunctors into the Cauchy completion of their codomain.
to
In general, right adjoint profunctors correspond to functors into the Cauchy completion of their codomain.
I think that’s what was meant here.
-
- CommentRowNumber32.
- CommentAuthorarbipher
- CommentTimeNov 5th 2024
The typesetting is broken on section 9. -
- CommentRowNumber33.
- CommentAuthorMatt Earnshaw
- CommentTimeNov 12th 2024
1 to 33 of 33