nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorTobyBartels
- CommentTimeApr 4th 2010
Possibly we need to go through the Lab and consistently use the term ‘quiver’ for a presheaf on
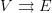 , which is the kind of graph that a strict category has as its underlying graph: directed, possibly infinite, possibly with loops, possibly with unequal parallel arrows.
, which is the kind of graph that a strict category has as its underlying graph: directed, possibly infinite, possibly with loops, possibly with unequal parallel arrows.We have used ‘digraph’ and ‘directed graph’ (and maybe even just ‘graph’) for this, for which there are arguments, but which is at best ambiguous and at worst wrong. We have also used ‘quiver’ for the free category on the graph, for which there are also arguments (much as we might conflate a preordered set with the co-free category on it), and we decided to stop that, but there might still be some examples of that usage around.
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Yes, I totally agree.
However, the thing about a quiver being a presheaf on that category, I've got a question. Isn't there a way to add more to that diagram to make any presheaf over it a legitimate category? Something like that you have to add an identity assigning morphism in the other direction and also have some composition rules as well? (Like if we require the base category to be look like the arrow-theoretic definition of an internal category.)
-
- CommentRowNumber3.
- CommentAuthorTobyBartels
- CommentTimeApr 4th 2010
Well, the 1-category Cat is not a topos, so there's no way to find any category C such that presheaves on C are categories (at least, not with functors as presheaf morphisms). Of course, you can get the definition of category if you start with presheaves on
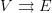 , then define strict categories as presheaves with certain extra structure. Or you can define a category as a limit-preserving presheaf on
, then define strict categories as presheaves with certain extra structure. Or you can define a category as a limit-preserving presheaf on 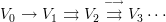 (a category which is not free on a quiver but whose laws I hope you can guess), which is similar to (but not quite an example of) a Lawvere theory.
(a category which is not free on a quiver but whose laws I hope you can guess), which is similar to (but not quite an example of) a Lawvere theory.But I mentioned presheaves only to have a quick and precise way to define what I meant without using any of the terms that I was trying to discuss. (^_^)
-
- CommentRowNumber4.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Yeah, I was thinking about it earlier, and I came to that exact same picture (wrt the picture that looks like
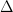 ).
).I saw a diagram describing homotopical descent in Toen's notes on stacks, and somehow he managed to stack up 7 arrows going back/forth/back/forth using LaTeX.
Was he using XYPic, or is there something like $\arrows{lrlrlrlr...}$ to add arrows that go back/forth (left right left right...) without xypic, or is it only single and double arrows?
-
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeApr 4th 2010
Interesting. Would an n-globular set then be an n-quiver?
-
- CommentRowNumber6.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
What do you mean by n-quiver?
-
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeApr 4th 2010
An n-globular set, of course! (-:
-
- CommentRowNumber8.
- CommentAuthorEric
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
"Quiver" seems to be a loaded word. Can we avoid using that word on diagram? I'd prefer to say
However, we often use the term ‘diagram’ for something that we can actually see on the page, in which case we mean a functor whose domain is the free category on a directed graph (often a finite one).
? Please? :)
Edit: I went ahead and made this change. Let me know if you want me to change it back (or just change it back, either way).
-
- CommentRowNumber9.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
No, because the word "directed graph" is incorrect, as Toby noted in the thread on quivers. The correct term is precisely quiver/multidigraph/diagram scheme. I have reverted the change.
-
- CommentRowNumber10.
- CommentAuthorEric
- CommentTimeApr 4th 2010
We had this discussion long ago before you were around around and for the purposes of the nLab, we "Played Bourbaki". A quiver is now a free category on a directed graph. This is pervasive throughout the nLab at this point.
And regardless of what "directed graph" may mean outside the nLab, for the purposes of the nLab a directed graph is precisely what it says it is at directed graph.
Are we going to have to rewrite the entire nLab whenever a new student joins in?
-
- CommentRowNumber11.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
No, this is incorrect. Toby agrees with me as well, as does every other standard source on the subject (including but not limited to every single reference document on the entry quiver, Wikipedia, and every single book that covers quiver representations). Also, your dismissive (and hypocritical) statement is not appreciated, Eric. You've made a rather drastic change over at the definition of functor, which has thrown a good deal of the nLab into circularity (although I admit that this is resolvable circularity, you can see the new thread that I've started and my argument about why this is not at all the direction in which we should go).
Then I pose the following question, are we going to rewrite the entire nLab every time you decide you don't like the way a notion is defined?
I'm dying to change the definition of a prestack so it makes sense, but this is unfortunately impossible because it is used in Algebraic geometry. Similarly, representation theory uses the word "quiver" to describe this concept. If I can't change prestack, a term that deserves to be changed much more than quiver, then changing quiver should be out of the question entirely!
-
- CommentRowNumber12.
- CommentAuthorEric
- CommentTimeApr 4th 2010
Then I pose the following question, are we going to rewrite the entire nLab every time you decide you don't like the way a notion is defined?
I was trying to answer this question on your "circular" thread while you were writing it here :)
No, we are not going to rewrite the entire nLab every time I decide I don't like the way a notion is defined. Rather, if a notion does not resonate with the way I'd prefer to think of it (which isn't to say the notion is wrong), I will ADD to the nLab so that others who might be similarly confused (and I assure you there are others just as confused as I am) might avoid some trouble.
I like the idea of defining functors as maps that "preserve commutative diagrams". It resonates with the way I think about things, but I would never remove the standard definition.
Regarding "quiver" vs "directed graph", I'd be ok with a global replacement of the word "directed graph" with "quiver" whenever we are talking about a presheaf on
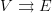 , but that is not how we started things. Note, that was precisely my first question on the discussion of quiver.
, but that is not how we started things. Note, that was precisely my first question on the discussion of quiver.Are we now saying that we want to undo John's "Bourbaki" renaming?
If that is the case, we should merge directed graph and quiver and put a redirect to graph for directed graph. I'm not entirely against the idea.
-
- CommentRowNumber13.
- CommentAuthorHarry Gindi
- CommentTimeApr 4th 2010
- (edited Apr 4th 2010)
Are we now saying that we want to undo John's "Bourbaki" renaming?
Precisely.
What we should do is change "directed graph" to "quiver", "quiver" to "free category on a quiver", and merge "free category" into this new article. However, let's wait for someone with authority to approve this change, as I don't want to be seen as acting unilaterally or forcing you to accept it.
A directed graph is a quiver with at most one edge between any two objects. This is the point of the "directedness" in the name. It means that you can't go backwards on the graph.
-
- CommentRowNumber14.
- CommentAuthorEric
- CommentTimeApr 4th 2010
I would not be opposed to such a change, but will defer to the experts as well.
I actually liked the terminology in your professor's notes: diagram scheme.
-
- CommentRowNumber15.
- CommentAuthorTobyBartels
- CommentTimeApr 4th 2010
@ Harry: Actually, that is not the point of ‘directed’ in the name. A quiver is also directed; it is a directed multigraph. And even in a simple directed graph, it is possible to have one edge going each way:
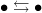
Anyway, that is a technicality; I'm guessing that you just didn't write what you meant to write?
@ Eric:
The term ‘quiver’ really is least ambiguous, I think. While ‘directed graph’ is often used by category theorists in the sense that we want, it is also used in the more restrictive sense that Harry indicates (that is a quiver with at most one edge from any one object to any other one object, and also many would demand no edge from any object to itself). But ‘quiver’ is used almost only for the sense that we want, and even using it for the free category on the graph can be seen as simply an abuse of language (or not even an abuse), identifying a graph with its free category (much as we identify a set with the discrete category on it).
-
- CommentRowNumber16.
- CommentAuthorHarry Gindi
- CommentTimeApr 5th 2010
- (edited Apr 5th 2010)
@Toby: I was thinking of an oriented (simple) graph =). -
- CommentRowNumber17.
- CommentAuthorEric
- CommentTimeApr 5th 2010
What do we call a "directed graph without composites"?
In a directed graph (as I use it... and as Humpty Dumpty would) we can have directed edges
 and
and  without having a directed edge
without having a directed edge  . This would never happen in a free category on a graph.
. This would never happen in a free category on a graph. -
- CommentRowNumber18.
- CommentAuthorTodd_Trimble
- CommentTimeApr 5th 2010
- (edited Apr 5th 2010)
You call it a ... directed graph. By definition, a directed graph has no (given) composition law.
If you want to know what do we call a directed graph for which there exists no composition law, then that's a different story, and I have no idea. But I don't think it would be a very useful concept; you couldn't build much of a theory around them. More rudely, I'd say they're really not worth thinking about. In Jonathan Vos Post's "Ideocosm", it'd be sitting in a landfill somewhere.
-
- CommentRowNumber19.
- CommentAuthorEric
- CommentTimeApr 5th 2010
There is an entire field call "graph theory" based on graphs without composition laws :)
identifying a graph with its free category
Statements like this confuse me because a directed graph doesn't need composites, but a free category does. So to get a free category from a directed graph, you need to "fill in" composites. So to identify a graph with its free category, you must be restricting yourself to special kinds of directed graphs, i.e. ones containing all composites.
In Urs and my paper we discussed "graphs without intermediate edges". They were critical for the entire formulation. What this means is that if your directed graph contains edges
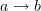 and
and 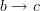 it CANNOT contain an edge
it CANNOT contain an edge  .
.you couldn't build much of a theory around them.
Then you haven't read our paper :) (But I don't blame anyone for that, it is not the easiest paper in the word to read. I hope to rewrite the gist one day (maybe from the nPOV) because I think it is important.)
The idea is that starting with a special kind of "directed graph without composites", big chunks of Lorentzian differential geometry essentially fall on your lap in a purely combinatorial way.
-
- CommentRowNumber20.
- CommentAuthorEric
- CommentTimeApr 5th 2010
- (edited Apr 5th 2010)
Sorry for quoting myself...
What this means is that if your directed graph contains edges
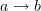 and
and 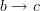 it CANNOT contain an edge
it CANNOT contain an edge  .
....but wanted to highlight an important point related to the above statement.
Although directed edges
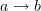 and
and 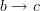 imply there cannot be an edge
imply there cannot be an edge  , it DOES imply the existence of a fourth node
, it DOES imply the existence of a fourth node 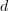 and two edges
and two edges 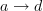 and
and 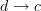 , i.e. the basic shape in our paper is a "directed cube" that we lovingly called a "diamond".
, i.e. the basic shape in our paper is a "directed cube" that we lovingly called a "diamond". -
- CommentRowNumber21.
- CommentAuthorHarry Gindi
- CommentTimeApr 5th 2010
Eric, your paper has nothing to do with the algebraic structure on the graph... -
- CommentRowNumber22.
- CommentAuthorEric
- CommentTimeApr 5th 2010
- (edited Apr 5th 2010)
How do you define "algebraic structure"? As far as I'm concerned it is nothing BUT algebraic structure on a directed graph. Any disagreement here must surely be semantic.
PS: I am impressed that Harry can read our paper and draw such a conclusion in less than 100 seconds :)
-
- CommentRowNumber23.
- CommentAuthorHarry Gindi
- CommentTimeApr 5th 2010
- (edited Apr 5th 2010)
Yes, I absolutely can tell that this paper does not deal with the _relevant_ kind of algebraic structure in 100 seconds. Whether or not it deals with what can be called algebraic structure on a graph is up to whether or not you consider homology and cohomology to be "algebraic structure on the graph". -
- CommentRowNumber24.
- CommentAuthorTodd_Trimble
- CommentTimeApr 5th 2010
Hm... I'm not sure that your question at #17 was very well posed then.
It sounds in #19 like you are considering the condition
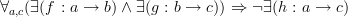 . Is that right? If so, that's a lot stronger than inexistence of a composition law on a directed graph, which is what I was guessing you might have been asking about in #17.
. Is that right? If so, that's a lot stronger than inexistence of a composition law on a directed graph, which is what I was guessing you might have been asking about in #17. -
- CommentRowNumber25.
- CommentAuthorEric
- CommentTimeApr 5th 2010
- (edited Apr 5th 2010)
Hi Todd. I asked about the softer condition in #17, i.e. graphs that may not have composites. You responded with something that sounded like you were saying such things were not interesting. I replied by saying that there were interesting graphs that were even stronger, i.e. no composites at all, in #19.
My point is that these graphs are interesting (which is a subjective statement I know) to Urs and I at least since these are the graphs our paper dealt with.
-
- CommentRowNumber26.
- CommentAuthorHarry Gindi
- CommentTimeApr 5th 2010
- (edited Apr 5th 2010)
Anyway, this is not really relevant. I haven't read the paper in detail, but it looks to me like you and Urs really meant an honest directed graph (at least from the pictures), since I did not see any loops or multiple arrows. -
- CommentRowNumber27.
- CommentAuthorTodd_Trimble
- CommentTimeApr 5th 2010
Point remains: I don't know what you call them. If you want to argue that something or other is interesting, go ahead -- but I really don't know what you're on about at this point. Sorry.
-
- CommentRowNumber28.
- CommentAuthorTobyBartels
- CommentTimeApr 10th 2010
@ Eric:
If you identify a quiver with its free category, you don't identify the edges of the quiver with the morphisms of the category; as you say, that would only be correct for very special quivers (in fact, only for the empty quiver!). Instead, you identify the edges of the quiver with the indecomposable morphisms of the category, and you identify paths of the quiver with the morphisms of the category. (A morphism
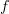 is indecomposable if, whenever
is indecomposable if, whenever 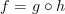 , then
, then 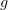 xor
xor 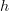 is an isomorphism.)
is an isomorphism.)Or put another way: Every category has an underlying quiver whose edges are the morphisms of the category, but we cannot simultaneously identify a quiver with its free category and a category with its underlying quiver, since it is simply not true that a quiver is isomorphic to the underlying quiver of its free category (except for the empty quiver). However, every category has another associated quiver, whose edges are the indecomposable morphisms of the category. And it is true that a quiver is isomorphic to the quiver of indecomposable morphisms of its free category. It is in this way that we may pass back and forth between a quiver and its free category.
-
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeApr 10th 2010
identifying a graph with its free category
Statements like this confuse me because a directed graph doesn’t need composites, but a free category does.
So let’s sort this confusion out: one often identifies some thing with very different things. That works as soon as we have a bijection between two different sets of things, that preserves the relevant structure of these things.
Here what we do is the following: we use the functor
to identify the collection of directed graphs with their image in .
It is not a particularly good identification, though, because this is not a full and faithful functor (it is not full). But this is what is meant.
-
- CommentRowNumber30.
- CommentAuthorDavidRoberts
- CommentTimeApr 11th 2010
And it is true that a quiver is isomorphic to the quiver of indecomposable morphisms of its free category
excellent: this is what Eric has been looking for. However, if I have
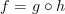 indecomposable, and
indecomposable, and 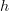 an isomorphism, then is
an isomorphism, then is 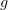 counted among the indecomposables? Would we rather pass to equivalence classes of indecomposables (in the obvious way -
counted among the indecomposables? Would we rather pass to equivalence classes of indecomposables (in the obvious way - 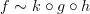 for
for 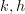 isomorphisms)
isomorphisms) -
- CommentRowNumber31.
- CommentAuthorTobyBartels
- CommentTimeApr 11th 2010
- (edited Feb 13th 2011)
Re #29
Note that this functor is full on isomorphisms. Mike Shulman would say that being (the free category of) a quiver is a property-like structure on a category, while I would say that is simply a property, but quiver morphisms and functors aren’t the same. (Specifically, a quiver morphism is a functor that preserves indecomposability.) More precisely, we have an embedding (an -functor that is -surjective for all ) between -groupoids , even though this does not extend to an embedding between -categories . (Note that happens to be a -category and a -category, so the reader may replace ‘’ with ‘’ if desired.)
Re #30
Good question! I can see two answers:
- Just use strict categories. After all, a free category on a quiver is naturally a strict category, and we need a strict category if we want to take its underlying quiver, so everything works if we just use strict categories everywhere.
- Modify (or phrase more carefully) the definition of the ‘quiver of indecomposables’ (if I may call it that) so that it is not evil: the set of vertices is the set of isomorphism classes of objects, and the set of edges is (as you suggested) the set of isomorphism classes of indecomposable morphisms.
H’m, this gives two definitions of the quiver of indecomposables; even applied to a skeleton, the latter definition may cause us to identify morphsisms which are not equal. I’m not sure whether it is best to use the non-evil operation or the evil operation that applies only to strict categories.
For the free category on a quiver, however, it makes no difference; in that strict category, every isomorphism is an identity.
(In a strict category, there are also two possible definitions of indecomposable: the one that I gave, and one where xor must be an identity; one may call such a morphism strictly indecomposable. So there are really three different notions of the quiver of indecomposables of a strict category, only one of which generalises to a non-evil operation on categories. But again, it makes no difference in the free category on a quiver; up to natural isomorphism, there is only one quiver of indecomposables of such a category, and it agrees with the original quiver.)
-
- CommentRowNumber32.
- CommentAuthorTodd_Trimble
- CommentTimeApr 11th 2010
That sounds correct to me, David. In this way, “indecomposables” are like prime elements in a principal ideal domain, and you suggestion is reminiscent of looking at prime ideals instead.
-
- CommentRowNumber33.
- CommentAuthorEric
- CommentTimeApr 11th 2010
Toby said:
you identify the edges of the quiver with the indecomposable morphisms of the category, and you identify paths of the quiver with the morphisms of the category. (A morphism is indecomposable if, whenever , then xor is an isomorphism.)
This sounds like a quiver is to a category what a Hasse diagram is to a poset. Is that right? In fact, would a quiver of a poset be a Hasse diagram? In case I got that wrong, in an attempt to avoid terminology confusion in the following, I will use the term “generalized Hasse diagram” for this analogue and if it is the same as “quiver”, I’ll start calling it quiver instead.
If so, that sounds like what I was trying to describe starting here. Then the map
described here (if it exists) sends a category to its generalized Hasse diagram as opposed to
which sends a category to its full underlying directed graph which includes composite edges.
I would be surprised if all categories admitted a “generalized” Hasse diagram like this, but happy if they did. In any case, I would be interested in knowing what kind of category admitted a generalized Hasse diagram.
By the way, I am happy to see a discussion about “indecomposables”. I think it is an interesting concept. I think some interesting categories do not have indecomposables. For example, the path category of a smooth manifold where objects are points and morphisms are paths. There, any path can be decomposed. Something I consider to be an undesirable feature.
-
- CommentRowNumber34.
- CommentAuthorHarry Gindi
- CommentTimeApr 11th 2010
Here what we do is the following: we use the functor
FreeCategory:DiGraph→Cat
to identify the collection of directed graphs with their image in Cat.
It is not a particularly good identification, though, because this is not a full and faithful functor (it is not full). But this is what is meant.
I thought that it was the forgetful functor that was faithful.
-
- CommentRowNumber35.
- CommentAuthorEric
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
By the way, this seems related to my comment here, which I will quote taking some liberty to fix some terms (since I used “quiver” to mean “free category of a graph”)
David mentioned something in that other thread about underlying graphs that illustrated an extra degree of confusion on my part. Given a category with 3 objects , , and and three non-identity morphisms , and , what is its underlying graph? There are two options I can think of (Edit: Ignoring identity morphisms):
- , , and , or
- and
What David said (if I understood correctly, which is always a big “if”) seemed to indicate the correct choice is 1.) , whereas I always thought it should be 2.). I always thought should be the “smallest” graph such that you can recover (or something “equivalent” in some way) when constructing the free category . I figured you wouldn’t need the directed edge in because this comes for free when you construct the free category of the TWO directed edges and .
Basically, two different directed graphs can have the same free category, so which one should you take as the underlying one? The “full one” (including all composite edges) or the “smallest” one (containing only non-composite edges)?
I should probably try to clear that up before moving on. Which is it? Is in ?
In the subsequent discussion, I accepted that 1.) was the correct choice. If I understand, Toby is talking about 2.) which is also interesting.
Then David came up with a nice example of a category with 3 objects , , and 3 non-identity morphisms forming a loop
implying the opposite loop is also there
The map 1.) is unambiguous, but the map 2.) involves a choice, i.e. the generalized Hasse diagram may not be unique.
-
- CommentRowNumber36.
- CommentAuthorEric
- CommentTimeApr 11th 2010
@Todd: Interesting observation! :)
Thinking about decomposables might somehow be related to thinking about primes. Hmm…
-
- CommentRowNumber37.
- CommentAuthorTobyBartels
- CommentTimeApr 11th 2010
Yes, I suppose that you could regard taking the quiver of indecomposables of a category as taking a generalised Hasse diagram.
For the vast majority of categories, of course, you cannot recover the category from its quiver of indecomposables. (So the generalised Hasse diagram may not describe the category correctly.) You can only do that for quivers (that is, for free categories on quivers). In fact, for quite a lot of categories, there are no indecomposable morphisms at all! So even when we identify quivers with certain categories, they are very special categories.
-
- CommentRowNumber38.
- CommentAuthorEric
- CommentTimeApr 11th 2010
I would be interested in knowing what kind of categories admit a generalized Hasse diagram.
The path category of a smooth manifold does not admit a generalized Hasse diagram because there are no non-decomposable morphisms.
A category with “loops” does not admit a unique generalized Hasse diagram because there will be three object loops, each with an opposite loop, and you can pick either one for the diagram.
It would seem that something along the lines of “small categories with countable set of objects and no loops” admit unique generalized Hasse diagrams. Maybe “countable directed spaces”?
-
- CommentRowNumber39.
- CommentAuthorTobyBartels
- CommentTimeApr 11th 2010
I would be interested in knowing what kind of categories admit a generalized Hasse diagram.
If what you call ‘a generalized Hasse diagram’ is the same thing as what I call a ‘quiver of indecomposables’, and if a category ‘admits a generalized Hasse diagram’ precisely when it is the free category on this quiver, then it is exactly the free categories on quivers that admit generalised Hasse diagrams.
For an example of a small category with a countable set of objects and no loops that does not admit a generalised Hasse diagram in this sense, take the category with three objects and four non-identity morphisms , , and . Its quiver of indecomposables is , but the free category on that quiver has five non-identity morphisms, with .
For an example of a large category with an uncountable set of objects and loops that does admit a generalised Hasse diagram in this sense, take the free category on any large quiver with a loop. More specifically, take the disjoint union of the delooping of the monoid and the discrete category on any large set; the generalised Hasse diagram of this category is the disjoint union of a vertex with a single loop and a large discrete graph.
I could be talked into not counting the last example as a generalised Hasse diagram, by adding restrictions on which quivers we accept as generalised Hasse diagrams, so you could convince me that a category that admits a generalised Hasse diagram must be small, with a countable set of objects and no loops. But I hope that you agree that my first example (the one with the picture) does not have a generalised Hasse diagram.
-
- CommentRowNumber40.
- CommentAuthorEric
- CommentTimeApr 11th 2010
But I hope that you agree that my first example (the one with the picture) does not have a generalised Hasse diagram.
Yes, I agree. It doesn’t have a generalized Hasse 1-diagram, but it has a generalized Hasse 2-diagram :)
I have formed an opinion (that might wrong) that a 1-diagram that does not commute implies the existence of a non-identity 2-morphism between the two paths. In your example, the little diagram does not commute so , which implies a non-identity 2-morphism so you really have a 2-category. A countable 2-category with no loops admits a generalized Hasse 2-diagram, i.e. a minimal directed 2-graph.
Maybe we should be talking about Hasse computads :)
-
- CommentRowNumber41.
- CommentAuthorTobyBartels
- CommentTimeApr 11th 2010
- (edited Feb 13th 2011)
Well, I do really have a -category; I hardly have any doubts about that. I could spell out its multiplication table in full detail, and we could check the associativity law, etc. Every -category can be interpreted as a -category, but there is no -morphism from to in that -category.
-
- CommentRowNumber42.
- CommentAuthorEric
- CommentTimeApr 11th 2010
Right right. Sorry. I stated that very poorly.
What I’m trying to say is that for a 1-category with noncommuting diagrams, there is an -category with “fillers” that fill any noncommutating diagram whose -diagrams commute such that the original category is a projection of this one.
This idea is inspired by Urs’ and Domenico’s discussion and making an analogy between “commutative diagrams” and “flat connections”.
Just as every connection is flat when viewed in a higher category, every diagram commutes when viewed in some higher category.
So there is a 2-category with 2-morphism fillers such that all 2-diagrams commute and your category is a projection. This means there are 2-morphisms and , but since this 2-diagram commutes, it means . There is a Hasse 2-diagram for this 2-category which projects down to your 1-category.
I hope that is a little better, but I imagine it still is pretty vague (maybe incomprehensibly so). Worse, what I said could be totally wrong…
-
- CommentRowNumber43.
- CommentAuthorHarry Gindi
- CommentTimeApr 11th 2010
Just as every connection is flat when viewed in a higher category, every diagram commutes when viewed in some higher category.
This is palpably false.
-
- CommentRowNumber44.
- CommentAuthorMike Shulman
- CommentTimeApr 11th 2010
Eric, I feel like we’ve told you a bunch of times that you can’t represent inequalities by morphisms in a higher category, because inequalities can’t be composed: if and , it doesn’t follow that . My apologies if you’re saying something different now, but it seems like the same thing to me.
-
- CommentRowNumber45.
- CommentAuthorEric
- CommentTimeApr 11th 2010
Hi Mike,
I think (hope!) I am saying something different. The composition of two non-identity 2-morphisms can be an identity 2-morphism. So implies a non-identity 2-morphism and implies a non-identity 2-morphism , but if , I don’t think there is a contradiction. If , it means the composite is the identity 2-morphism, i.e. .
Then, in case , this implies a non-identity 2-morphism AND a non-identity 3-morphism .
The picture here is very pretty. I would be sad if there was no truth to it.
From what I can tell, this is a pure analogy to Urs’ and Domenico’s discussion of flat connections. A non-flat 1-connection is a projection of a flat 2-connection. A noncommuting 1-diagram is a projection of a commuting 2-diagram. If a 2-connection is not flat, you can fill it to obtain a flat 3-connection. If a 2-diagram does not commute, you can fill it to obtain a commuting 3-diagram. It is very pretty. I wish I could express myself better…
-
- CommentRowNumber46.
- CommentAuthorEric
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
PS: I am going to reproduce Domenico’s comment here since it is so cool
I guess this is well known, but let me try writing it here and see what happens.
If a connection on a principal -bundle is locally represented by the 1-form with values in , then the connection is flat if and only if the curvature 2-form vanishes, that is, if is a solution of the Maurer-Cartan equation.
Now, what is interesting is that one can see curvature only on 2-dimensional paths (it is a 2-form): if one restricts to a 1-dimensional submanifold, then there is clearly a solution to the Maurer-Cartan equation. so, if I think of an infinitesimal 1-simplex and look at my connection there, I could say that my connection is 1-flat. then, moving to an infinitesimal 2-simplex I see that the connection is (generally) not 2-flat: holonomy along two sides of the 2-simplex is not the same thing as holonomy along the third side. not the same, but in a very precise way: the curvature exactly measures the gap to go from a horn of the 2-simplex to the third edge. this is very 2-categorical, and suggests I could cure the lack of flatness of my original connection by adding a copy of in degree -1 and cooking up a 2-Lie algebra . Maurer-Cartan equation for this 2-Lie algebra would coincide with the original one one the 1-simplex (since only degree 1 elements are 1-forms with values in . but on the 2-simplex we would have, in addition to these elements, also 2-forms with coefficients in , and the Maurer-Cartan equation on teh simplex would look like where is the differential of the -algebra (and it should be induced by the identity of , thought as a degree 1 map from to ). So the original equation telling that had curvature is now equivalent to say that is flat.
in other words, what seemed a non-flat connection was so since I was not seeing the 2-bundle, but only a 1-bundle approximation. and on a 1-bundle I can only clearly see up to 1-simplices, wher my connection was actually flat.
once curvature has come in, we can repeat the argument: now we have a 2-flat connection and test it on the 3-simplex. if it has 3-curvature, that will presumibly be because we are not seeing the 3-bundle, yet. so I find it natural to wonder (to conjecture) whether any connection on a principal bundle (and more generally any -flat connection on an -bundle) can be seen as a flat connection on an -bundle.
What I’m talking about is trying to be a simplified version of this where instead of talking about trivial holonomies, i.e. flat connections, we are talking about commuting diagrams (which I think are closely related)
We can “test” all 1-diagrams to see if they 1-commute. If one does not, we can “fill” it with 2-morphisms to make the individual filled 2-diagram 2-commute. Then we can test all subsequent 2-diagrams to see if they 2-commute. If one does not, we can fill it with 3-morphisms to make it 3-commute. Etc etc.
Something like that anyway…
PS: The prescription chosen for “filling” a category like this could be called something like the “-curvature of an -category”, where the category itself is essentially an -connection.
-
- CommentRowNumber47.
- CommentAuthorHarry Gindi
- CommentTimeApr 11th 2010
- (edited Apr 11th 2010)
What???
Eric, you should give the first chapter of HTT a shot before you try to formulate this definition. It appears that you're trying to formulate the definition of a quasicategory, but you aren't really doing it right. It would save you and us a lot of time if you paged through HTT.
-
- CommentRowNumber48.
- CommentAuthorTobyBartels
- CommentTimeApr 11th 2010
@ Eric
I’m trying to understand the -category that you propose in response to my example of a category with no generalised Hasse diagram in #39. You would put in -morphisms and , yes? And based on your comment #45, I think that you would also have (since ) and (since ). And I guess that the whiskerings and should be the identity on .
OK, now we have a strict -category, that’s fine. But this strict -category is equivalent (as a strict -category) to (the -category produced from my example by identifying and , interpreted as a -category). This is because and are isomorphisms (since they have inverses: each other), so they serve to identify and up to isomorphism. Yet in my original -category, and are as distinct as distinct can be; they should not be made isomorphic. So your -category (if I understand it) doesn’t really have much to do with my -category.
Even if it is relevant, I don’t see how you can expect to get this -category from some sort of -quiver. After all, it has loops: and .
I want to repeat that I agree with your remark at the beginning of comment #38 that it is interesting to ask which categories admit generalised Hasse diagrams. I just don’t agree with your answer to that question at the end of comment #38.
-
- CommentRowNumber49.
- CommentAuthorMike Shulman
- CommentTimeApr 12th 2010
Toby said what I was going to say: if you have a unique identity 2-morphism between equal arrows, and a unique nonidentity morphism between unequal arrows, then any two arrows are uniquely isomorphic, so your resulting 2-category is equivalent to a poset. So at least if you want to treat this 2-category 2-categorically, then it is not encoding the difference between equality and inequality of arrows.
-
- CommentRowNumber50.
- CommentAuthorEric
- CommentTimeApr 12th 2010
- (edited Apr 12th 2010)
Thanks Toby and Mike.
I need to take a step back in the lab maze because I took a wrong turn, but I still think the idea is pretty. I’m just failing to say it correctly.
I added the second 2-morphism at the last minute as I was typing. I should probably spend some time on my wikiweb to think this through. I understand now that having both would mean and are equivalent, so my immediate thought is that we should not keep both. We should fill the diagram with just 1 2-morphism (as I originally had in mind).
I think what I’m trying to do should somehow be related to computads. I think I mentioned somewhere the idea could probably be described as a “Hasse computad”.
-
- CommentRowNumber51.
- CommentAuthorMike Shulman
- CommentTimeApr 12th 2010
Are you saying that if , you want to have a 2-morphism but not ? That seems problematic, given that inequality is a symmetric relation; how do you “tell” which direction the 2-morphism goes?
-
- CommentRowNumber52.
- CommentAuthorEric
- CommentTimeApr 12th 2010
Yep yep. That is one thing I need to think about.
I printed out some papers on computads and skimmed them on the way home. I also had another look at Street’s AOS paper again. I drew some pictures…
If you were to think of Toby’s example
as a “space”, would you think of it as a loop on a handle (like the metal of a magnifying glass) with empty space between and or as a solid paddle with the space between and filled? If you know what I mean, which I would be surprised if you did since that is so vague…
-
- CommentRowNumber53.
- CommentAuthorDavidRoberts
- CommentTimeApr 13th 2010
Empty space between f and g. Don't forget that everything needs to work for groupoids also, if you claim it for all categories, and so should be interpretable as a space with only
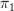 non-trival (for various basepoints if not connected). Then non-equal arrows should correspond to holes in the space. And adding even non-invertible higher arrows plays absolute havoc with the space (well, the homotopy type), because then these add non-trivial homotopy groups in (potentially) an infinite number of dimensions.
non-trival (for various basepoints if not connected). Then non-equal arrows should correspond to holes in the space. And adding even non-invertible higher arrows plays absolute havoc with the space (well, the homotopy type), because then these add non-trivial homotopy groups in (potentially) an infinite number of dimensions. -
- CommentRowNumber54.
- CommentAuthorEric
- CommentTimeApr 13th 2010
Thank you David. That helps me a lot more than you might think. Although throwing a symbol in there doesn’t help my intuition much, but this statement makes a lot of sense:
Then non-equal arrows should correspond to holes in the space.
I’ve been thinking about non-equal parallel arrows as “paddles” with the hole filled in. So, as everyone already knew from the beginning, my idea was doomed.
Maybe now we can get back to what Toby said:
I want to repeat that I agree with your remark at the beginning of comment #38 that it is interesting to ask which categories admit generalised Hasse diagrams.
-
- CommentRowNumber55.
- CommentAuthorMike Shulman
- CommentTimeApr 13th 2010
What is the definition of “generalised Hasse diagram” and when does a category admit one? I wasn’t quite clear from the previous discussion – does it just mean that the category is free on a quiver? If so, then I’m not sure what more of an answer one could expect than “those categories which are free on quivers.”
-
- CommentRowNumber56.
- CommentAuthorDavidRoberts
- CommentTimeApr 13th 2010
A related question: is there a characterisation (algebraic, say) of a free category without saying it is in the essential image of the free category functor
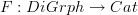 ? I should hope so.
? I should hope so. -
- CommentRowNumber57.
- CommentAuthorEric
- CommentTimeApr 13th 2010
- (edited Apr 13th 2010)
@David #56: That is a good question. A “free category” should be a category (I hope), and thinking of this example is probably what made me think the image of a functor (i.e. a diagram) should be a category. Is there something special about an adjoint functor that makes its image “essential”. I’m guessing (in the 2 minutes I have to think about this before asking my question) that “essential image” means the image is an object of the target category, so should be a category.
PS: Ok! I spent an extra 60 seconds checking essential image to verify this.
PPS: If the image of an adjoint functor is always “essential”, that would be a neat bit of trivia we could add to the respective nLab pages.
PPPS: Apologies in advance if I totally botched this.
-
- CommentRowNumber58.
- CommentAuthorDavidRoberts
- CommentTimeApr 13th 2010
I may not have meant essential image exactly. I meant the collection of objects in the image of the object component of the functor, together with all objects isomorphic to something in the image. An instructive example to think of (I hope) is vector spaces, and the functor
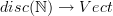 sending
sending  to
to 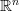 . Then the analogue of what I was talking about in the free category case is all finite dimensional vector spaces, not just the collection of
. Then the analogue of what I was talking about in the free category case is all finite dimensional vector spaces, not just the collection of 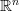 s. Note that
s. Note that 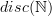 here is the category with set of objects
here is the category with set of objects 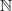 and only identity arrows.
and only identity arrows.Sorry for confusing the issue. :)
-
- CommentRowNumber59.
- CommentAuthorDavidRoberts
- CommentTimeApr 13th 2010
We'll just leave the essential image bit alone - it's not necessary here and not what I meant at all :S
-
- CommentRowNumber60.
- CommentAuthorMike Shulman
- CommentTimeApr 13th 2010
You could probably say something like “there exists a set of indecomposable morphisms such that every morphism factors uniquely as a composite of indecomposables.”
-
- CommentRowNumber61.
- CommentAuthorDavidRoberts
- CommentTimeApr 13th 2010
Not as a sort of 'there hold no non-trivial relations' type statement? Or perhaps what you wrote is that sort of thing, and I need to think about it a bit first. hmmm.... <thinks>
(PS: I'm not necessarily thinking of a small category, but of course that's immaterial for the present) -
- CommentRowNumber62.
- CommentAuthorMike Shulman
- CommentTimeApr 13th 2010
I would think of a uniqueness of factorization into indecomposables as being that sort of thing.
-
- CommentRowNumber63.
- CommentAuthorDavidRoberts
- CommentTimeApr 13th 2010
Yes, I think you're right. Because any relation can be expanded out uniquely as a relation between indecomposables, and by uniqueness this will be a trivial relation. Cool! -
- CommentRowNumber64.
- CommentAuthorzskoda
- CommentTimeApr 13th 2010
I should say that I did not follow details on quiver basic here, but I got from my student Matija who was recently at a winter school on representation theory that as soon as he finishes few homeworks due soon, he plans to start doing a bit of nlabing starting with filling few entries on the role of quivers in the rep theory of fin dimensional algebras, I mean things like tilted modules, Auslander-Reiten theory and so on. He delivered a couple of seminars in Zagreb on this and I was too busy and hence missed the second one.
-
- CommentRowNumber65.
- CommentAuthorEric
- CommentTimeApr 14th 2010
Awesome!
1 to 65 of 65