nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeApr 5th 2010
- (edited Apr 5th 2010)
Just in case anyone is wondering:
I am back from a small vacation. Will probably not have much time to catch up with accumulated discussion here, but maybe a bit.
-
- CommentRowNumber2.
- CommentAuthorIan_Durham
- CommentTimeApr 5th 2010
Hope you had a nice vacation! -
- CommentRowNumber3.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 6th 2010
me back, too :)
relaxed and eager to add a new bit to structures in an (oo,1)-topos. today's challenge is.. cobordims! I feel we have discussed path groupoids enough to be ready for this further step. we've been discussing something related here but remaining somehow halfway. -
- CommentRowNumber4.
- CommentAuthorEric
- CommentTimeApr 6th 2010
What is this thing called "vacation" of which you speak? :)
Welcome back :)
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeApr 6th 2010
- (edited Apr 6th 2010)
relaxed and eager to add a new bit to structures in an (oo,1)-topos.
Okay, good! :-)
today's challenge is.. cobordims! I feel we have discussed path groupoids enough to be ready for this further step. we've been discussing something related here but remaining somehow halfway.
There are some loose ends that me personally I need to tie up, and be it only to write them up. Right this moment I am polishing differential cohomology in an (oo,1)-topos.
Concerning cobordisms:
I am interested in the following slight variant of the usual lore:
we know that dual to cobordism representations is factorization algebras on cobordisms. I happen to know from my work on AQFT that functors out of the path oo-groupoid of paths in a given cobordism give rise, if the cobordism is equipped with a Lorentzian structure, to a "Lorentzian factorization algebra" (a local net of algebras).
The way this works suggests that one wants to do the following: consider a Lorrentzian manifold
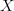 as a smooth poset, namely an
as a smooth poset, namely an 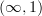 -category valued presheaf on CartSp whose plots in degree 0 are smooth spacelike maps
-category valued presheaf on CartSp whose plots in degree 0 are smooth spacelike maps 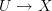 , and whose plots in degree 1 are U-families of future-directed paths.
, and whose plots in degree 1 are U-families of future-directed paths.Then the definition of path oo-groupoid of an oo-stack/
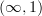 -sheaf generalizes to this
-sheaf generalizes to this 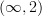 -sheaf situation, and we find a smooth oo-category whose k-morphisms are something like these causal subsets used everywhere in AQFT.
-sheaf situation, and we find a smooth oo-category whose k-morphisms are something like these causal subsets used everywhere in AQFT.I would like eventually to think about how to produce representations of n-categories of Lorentzian cobordisms from representations of these Lorentzian path oo-groupoids by taking some colimit or something.
-
- CommentRowNumber6.
- CommentAuthorEric
- CommentTimeApr 6th 2010
The finite version of this, of course, being
 -diamonds :)
-diamonds :)I'll be curious to see if you just need "future" directed paths or if "piecewise lightlike" directed paths somehow work out nicer. My gut tells me the latter...
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeApr 6th 2010
- (edited Apr 6th 2010)
I'll be curious to see if you just need "future" directed paths or if "piecewise lightlike" directed paths somehow work out nicer. My gut tells me the latter...
Right, I am still experimenting. But I think what I really meant to refer to above is really just morphisms in the poset that underlies the (globally hyperbolic, say) Lorentzain spacetime, i.e. just pairs of points with one in the future of the other.
Somehow the causal diamond should appear from this by some universal construction. Because every open subset in a (globally hyperbolic) Lorentzian spacetime has this universal causal hull, which is the intersection of all the complements of the lightcones of all its points. Somehow this must have a good and simple poset-categorical description...
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeApr 6th 2010
Somehow the causal diamond should appear from this by some universal construction.
Sorry for being so vague, i was distracted by something else. Of course given any set of points in the Lorentzian spacetime, regarded as a poset whose morphism are precisely the pairs of points where one is in the future of the other, the causal subsets are precisely the limit and colimit cones (joins and meets) over that set.
-
- CommentRowNumber9.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 6th 2010
what I had in mind was something less structured, i.e., without a Lorentian structure on the target manifold. basically, I was thinking of the 1-path groupoid of a differential manifold X; (suitably regular) representations of this groupoid in finite dimensinal vector spaces are finite rank vector bundles on X endowed with a connection. but once we have this datum, we can naturally extend it to a 1-dimensional QFT on X, with traces of holonomy assigned to loops in X (Wilson lines). having chosen finite dimensional vector spaces hides the difficulties connected with duals (every finite dimensional vector space is a fully dualizable object in the sense of Lurie).
in some very confuded way, all this suggests me that there should be a parametrized version of the cobordism hypothesys -
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeApr 6th 2010
- (edited Apr 6th 2010)
Domenico,
yes, I know what you mean. There is a bit of discussion of what one might expect here, precisely along the lines you just indicated, in the query box here.
I am still interested in that approach, too.It just occurred to me that I might be able to say more interesting things about that variant that I mentioned. What is interesting about that variant is that it differs from most (all) of the other discussion of higher categorical QFT in that it does make sense for Lorentzian signature. And in fact crucially depends on it. This is an interesting aspect all by itself that eventually deserves to be expounded on more.
-
- CommentRowNumber11.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 6th 2010
Urs,
yes, I'm familiar with that query box there.. :-)
what I was missing at that time was in which sense the QFT built from a vector bundle equipped with a connection was canonical. this canonicity was for me a "how else would you extend it?" but I was lacking canonicity of the construction in the rigorous sense. but now I have a hint: when we look at a vector bundle with a connection as a representation , we are forgetting about the tensor structure on Vect. the extended functor , instead, is a tensor functor. so, by saying that the datum of the latter representation is the same thing as the datum of the representation , we are giving a universal property, and we are saying something like is the free tensor category generated by .
this seems to hint to a natural generalization for X an object in an arbitrary (smooth) (oo,1)-topos -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeApr 6th 2010
something like
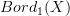 is the free tensor category generated by
is the free tensor category generated by 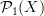 .
.That's an interesting thought. Maybe it's not the free tensor category, but the free tensor category with duals for objects. Because it is these duals that give the basic morphisms missing in
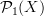 . For instance the path category cannot regard a path as a morphism from the empty object to the union of its two endpoints (with orientation). It's precisely the step of giving every point a dual object that makes this work.
. For instance the path category cannot regard a path as a morphism from the empty object to the union of its two endpoints (with orientation). It's precisely the step of giving every point a dual object that makes this work.Notice that something like this is correct for the case that
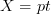 . Because in that case
. Because in that case 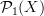 is itself the point, and by the cobordism hypothesis-theorem we know that
is itself the point, and by the cobordism hypothesis-theorem we know that 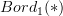 is something like the free
is something like the free 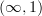 -category with some such properties.
-category with some such properties.Hm, so that's an interesting thoought, then. There must be still a bit more fine-print, since in the case with
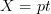 we know that not every parallel transport -- which is just a choice of a single object -- extends to a cobordism representation, but it needs to be a "fully dualizable" object, e.g. a finite dimensional veector space. So it can't be quite true that
we know that not every parallel transport -- which is just a choice of a single object -- extends to a cobordism representation, but it needs to be a "fully dualizable" object, e.g. a finite dimensional veector space. So it can't be quite true that 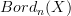 is simply the image of a left adjoint to the functor that forgets just monoidal structure. But something close might be true. Hm...
is simply the image of a left adjoint to the functor that forgets just monoidal structure. But something close might be true. Hm... -
- CommentRowNumber13.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 6th 2010
- (edited Apr 8th 2010 by Mathforge Admin)
not the free tensor category, but the free tensor category with duals for objects
for sure! my fault: I tend to call them just monoidal when they have not duals. -
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeApr 6th 2010
- (edited Apr 6th 2010)
I have this half-dormant project to think about oo-stacks with values in dendroidal sets, i.e. dendroidal set-valued presheaves satisfying some descent condition.
Together with Thomas Nikolaus we have pretty much convinced ourselves that a dendroidal set that fills all inner horns and all outer corolla horns is precisely one coming from an symmetric monoidal (oo,1)-category. This should be useful for speaking about
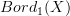 including both its smooth structure as well as its symmetric monoidal structure: the smooth structure is encoded in the presheaf of dendroidal sets, the monoidal structure in the fact that these dendroidal sets are objectwise symmetric monoidal (oo,1)-categories.
including both its smooth structure as well as its symmetric monoidal structure: the smooth structure is encoded in the presheaf of dendroidal sets, the monoidal structure in the fact that these dendroidal sets are objectwise symmetric monoidal (oo,1)-categories. -
- CommentRowNumber15.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 6th 2010
- (edited Apr 8th 2010 by Mathforge Admin)
So it can't be quite true that is simply the image of a left adjoint to the functor that forgets just monoidal structure. But something close might be true.
right. the cobordism hypothesis can be stated as follows: "given a symmetric monoidal (oo,n)-category with duals , evaluation of a functor on the point is an equivalence of (oo,n)-categories". but we can straightforwardly rewrite this as " is is an equivalence of (oo,n)-categories", which seems to be an -truncated version of some more general statement like
is is an equivalence of oo-categories", which could be a tentative definition of for an object in an (oo,1)-topos.
ok. now it's better I go and study what a dendroidal set is. -
- CommentRowNumber16.
- CommentAuthorDavidRoberts
- CommentTimeApr 7th 2010
@Domenico, no 11
Welcome back (and you too, Urs).
the extended functor
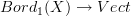 , instead, is a tensor functor. so, by saying that the datum of the latter representation is the same thing as the datum of the representation
, instead, is a tensor functor. so, by saying that the datum of the latter representation is the same thing as the datum of the representation 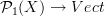 , we are giving a universal property, and we are saying something like
, we are giving a universal property, and we are saying something like 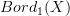 is the free tensor category generated by
is the free tensor category generated by 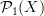 .
.I was discussing precisely this yesterday with a fellow student at uni. But I'm not sure that "
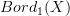 is the free tensor category generated by
is the free tensor category generated by 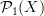 ", as the arrows in
", as the arrows in 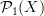 are thin homotopy classes and include back-trackings and the like. Actually, I'm not sure I know the definition of
are thin homotopy classes and include back-trackings and the like. Actually, I'm not sure I know the definition of 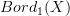 , so I can't make too much comment, but I would imagine it is something like paths mod reparameterisations. Help, someone!
, so I can't make too much comment, but I would imagine it is something like paths mod reparameterisations. Help, someone! -
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeApr 7th 2010
- (edited Apr 7th 2010)
Yes, there is some fine-tuning necessary here to make this anywhere close to being precise. But notice that the
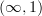 -category
-category 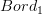 itself contains difeomorphisms as its higher morphisms, so
itself contains difeomorphisms as its higher morphisms, so 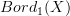 should similarly have cells that divide out reparameterizations.
should similarly have cells that divide out reparameterizations.What exactly we mean by
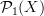 in this context is also a question. I would think a natural guess is to take the simplicial presheaf
in this context is also a question. I would think a natural guess is to take the simplicial presheaf ![[\Delta^\bullet_{Diff}, X] [\Delta^\bullet_{Diff}, X]](/extensions/vLaTeX/cache/latex_2cc16e5953a57d938883e096e0f7b014.png) or similar (details at path oo-groupoid) and then pass to its fibrant replacement not in the model category for oo-groupoid valued stacks on CartSp, but in that for (oo,1)-category valued stacks (the left Bousfield localization of the model structures of presheaves on
or similar (details at path oo-groupoid) and then pass to its fibrant replacement not in the model category for oo-groupoid valued stacks on CartSp, but in that for (oo,1)-category valued stacks (the left Bousfield localization of the model structures of presheaves on 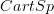 with values in the model structure for Cartesian fibrations over the point).
with values in the model structure for Cartesian fibrations over the point).That will produce the smooth path (oo,1)-category of X. I imagine that this would be the gadget that is most directly related to whatever precise definition for
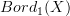 one uses.
one uses. -
- CommentRowNumber18.
- CommentAuthorDavidRoberts
- CommentTimeApr 7th 2010
- (edited Apr 7th 2010)
Well I was thinking of having
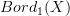 as a 1-category for a start ;-) (and
as a 1-category for a start ;-) (and 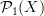 would be the usual thing, paths mod thin homotopy).
would be the usual thing, paths mod thin homotopy).Here's a trial definition of (the 1-cat)
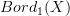 - I don't claim this is new, I'm just writing down what comes to mind: Objects are pairs
- I don't claim this is new, I'm just writing down what comes to mind: Objects are pairs 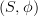 where
where 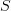 is an object of
is an object of 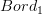 (i.e. a finite collection of oriented points) and
(i.e. a finite collection of oriented points) and 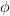 is a map
is a map 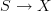 . Arrows are equivalence classes of pairs
. Arrows are equivalence classes of pairs 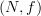 where
where 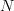 is a representative from of an arrow from
is a representative from of an arrow from 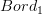 (a 1-dim oriented manifold with boundary) an
(a 1-dim oriented manifold with boundary) an 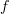 is a map from
is a map from 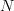 to
to  . Two of these
. Two of these 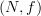 ,
, 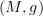 are equivalent if there is an orientation preserving diffeomorphism
are equivalent if there is an orientation preserving diffeomorphism 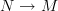 commuting with
commuting with 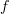 and
and 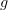 . Composition is the usual composition of cobordisms. The monoidal product is the usual one.
. Composition is the usual composition of cobordisms. The monoidal product is the usual one. -
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeApr 7th 2010
- (edited Apr 7th 2010)
Sure, something like this. Possibly with some extra discussion of what you do about collars and how exactly to glue/compose.
-
- CommentRowNumber20.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 7th 2010
- (edited Apr 7th 2010)
I agree. now let's see if we can define a functor (1-categorically, with David's definitions). objects in are maps , i.e., points of ; these are almost objects of , but they lack orientation (and no arbitrary choice of orientation works since inverting the verse of a path between two points should invert their orientation). next, a morphism in is the thin homotopy class of a smooth map . the naive attemp is to choose a representative for this class and look at this as a morphism in . but this would not work, since two thin homotopic maps need not be related by a reparametrization. the basic example of this is the "folding", given by a map which is some path between and and then goes backwards along the same path between and : this is thin homotopic to the constant map, but its not a reparametrization of the constant map!
on the other hand, reparametrization equivalent maps are thin homotopic, so thing could be better read the other way round: contains the submonoid of maps and this has a natural functor to . so in order to "extend" a representation of to a tensor functor out of one should first pull-back to and then "really" extend to .
I am now wondering if there really are representations of into Vect which are not arising from representations of (i.e., from vector bundles with connections), and if so how they are done. their trademark would be that the automorphism associated with folding is nontrivial. -
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeApr 7th 2010
two thin homotopic maps \Delta^1\to X need not be related by a reparametrization
That's why I suggested above to use the path category instead of the path groupoid (only that I said
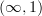 -category...). This is obtained by dividing out just reparameterization-preserving diffeos of the interval.
-category...). This is obtained by dividing out just reparameterization-preserving diffeos of the interval.That matches then pretty literally the quotient that David recalled above is used to define the morphisms in
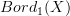 .
. -
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeApr 7th 2010
In fact, for all matters of parallel transport with values in groups (groupoids), functors out of the path category are just as well as functors out of the path groupoid: a smooth functor from the path category to
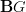 will factor through the path groupoid. (This is not meant to be tautologically
obvious.)
will factor through the path groupoid. (This is not meant to be tautologically
obvious.)So, to sketch the scene, I am imagining that the general statement might be that the
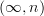 -category
-category 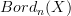 (or
(or 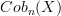 or whatever) is something like the free sheaf of symmetric monoidal
or whatever) is something like the free sheaf of symmetric monoidal 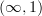 -categories with all duals on something lilke the sheaf
-categories with all duals on something lilke the sheaf ![\tau_n P [\Delta^\bullet_{Diff}, X] \tau_n P [\Delta^\bullet_{Diff}, X]](/extensions/vLaTeX/cache/latex_3ae85a6d00b38be4f9945ca613b15b27.png) , where
, where  denotes fibrant replacement in
denotes fibrant replacement in 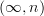 -category valued stacks and
-category valued stacks and 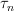 is
is  -truncation.
-truncation.Hm, well, this needs further qualification to make good sense, but something like this seems to be what we are conjuring here.
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeApr 7th 2010
- (edited Apr 7th 2010)
One more comment:
if we take the path n-category whose (equivalence classes of) n-morphisms are homotopy classes of n-dimensional paths, then this n-path
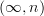 -category should have a very intrinsic characterization:
-category should have a very intrinsic characterization:namely: we ought to want to be saying that
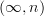 -sheaves on something like CartSp form a locally contractible
-sheaves on something like CartSp form a locally contractible 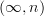 -topos
-topos 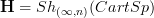 , for which the constant
, for which the constant 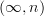 -stack functor
-stack functor 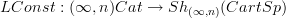 has a left adjoint
has a left adjoint 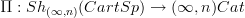 .
.This
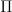 would be our bare path
would be our bare path 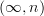 -category. It would generally be very interesting to understand what its free completion to monoidal thing with duals would be.
-category. It would generally be very interesting to understand what its free completion to monoidal thing with duals would be. -
- CommentRowNumber24.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 7th 2010
- (edited Apr 8th 2010 by Mathforge Admin)
oh, fine! I had missed the distinction :-( so the 1-path category seems to be what I called above, and then what we are saying perfectly agrees :-)That's why I suggested above to use the path category instead of the path groupoid
In fact, for all matters of parallel transport with values in groups (groupoids), functors out of the path category [...] obvious.)
this is a technical point I was missing, thanks! I can imagine a proof (basically one needs only to prove that the folding morphism has to be the identity), but can you address me to a reference? -
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeApr 7th 2010
and then what we are saying perfectly agrees :-)
Right!
but can you address me to a reference?
An argument is sketched in appendix B of
Freed, Classical Chern-Simons theory, Part I
that smooth parallel transport with values in
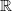 over paths has to come from integrating a 1-form, even without using quotients by thin homotopy.
over paths has to come from integrating a 1-form, even without using quotients by thin homotopy.It seems that also Dumitrescu's Connections and parallel transport does not use thin-invariance.
I had never much looked into this variant of the question, since I had always concentrated on path groupoids, but when I look at the proof in our Parallel transport and functors again, I guess it is true that where the 1-form is derived from the parallel transport, in fact the thin-invariance is not used. This just comes in because by decree this works with groupoids, not with categories.
-
- CommentRowNumber26.
- CommentAuthordomenico_fiorenza
- CommentTimeApr 7th 2010
- (edited Apr 7th 2010)
so, a smooth representation of with values in (finite dimensional) vector spaces is a (finite rank) vector bundle with a connection, and so is the datum of a principal -bundle with a -connnection, and of the defining representation of . this suggests that more generally a linear representations of with gauge group is the datum of a principal -bundle on with a -connection and a linear representation of . next step is considering linear representations of with a a gauge group. these should involve a Lie 2-group, a 2-principal bundle, a 2-connection, and a linear 2-representation.
mmm.. the string group is a Lie 2-group.. I feel scent of a Chern-Simoons gerbe here.. -
- CommentRowNumber27.
- CommentAuthorAndrew Stacey
- CommentTimeApr 7th 2010
(Incidentally, this is an example of a discussion with a - now - completely inappropriate title!)
-
- CommentRowNumber28.
- CommentAuthorDavidRoberts
- CommentTimeApr 8th 2010
Just a quick remark: Taking the path category
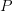 (called
(called ![[\Delta^1,X] [\Delta^1,X]](/extensions/vLaTeX/cache/latex_27755b06e1e8a65a958343f67c28d1f0.png) by Domenico above) and a functor
by Domenico above) and a functor 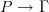 for some groupoid
for some groupoid 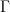 , then this factors through the category of fractions
, then this factors through the category of fractions ![P[Mor(P)^{-1}] P[Mor(P)^{-1}]](/extensions/vLaTeX/cache/latex_2fccef61b4c3fec81354cf1a75866d7c.png) . I'll have a think about this today and see what it looks like. I agree with Andrew, and let us continue this discussion in this thread.
. I'll have a think about this today and see what it looks like. I agree with Andrew, and let us continue this discussion in this thread.
1 to 28 of 28