Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory object of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: coinductive Trimble oo-categories

Bottom of Page

1 to 26 of 26

  1.  
    • CommentRowNumber1.
    • CommentAuthorMike Shulman
    • CommentTimeApr 6th 2010

    I added some comments to Trimble n-category regarding a coinductive way to state the definition, which I think is very clean and neat, and also a little mind-blowing.

    • CommentRowNumber2.
    • CommentAuthorMike Shulman
    • CommentTimeApr 6th 2010

    Oh, and I removed one of the query-boxes on that page and incorporated what I thought were the main interesting remarks into the main text. I think some of the other query boxes there could also be profitably removed.

    • CommentRowNumber3.
    • CommentAuthorTodd_Trimble
    • CommentTimeApr 6th 2010

    Thanks, Mike! That coinductive definition is pretty wild, and takes a while to grok -- I think it ought to be written up in a more leisurely way (with more examples of coinductive reasoning along the way). By the way, Tom Leinster and Eugenia Cheng are apparently writing out some sort of account of Trimble \omega-categories, and I think they would enjoy hearing about this clever way of formulating it.

    Incidentally, it bothers me that the homotopy hypothesis is still open for Trimble n-categories or \omega-categories, since they were pretty explicitly invented with this sort of application in mind. Perhaps you have some ideas about this? :-)

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeApr 6th 2010
    • (edited Apr 6th 2010)

    Incidentally, it bothers me that the homotopy hypothesis is still open for Trimble n-categories or \omega-categories, since they were pretty explicitly invented with this sort of application in mind. Perhaps you have some ideas about this?

    One should think about natural candidates for cosimplicial Trimble \omega-categories that would induce a nerve/realization adjunction.

    A reasonable guess seems to be that this is given by a composite of Street's orientals 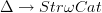\Delta \to Str \omega Cat with some cofibrant replacement Str \omega Cat \to Trimble \omega Cat .

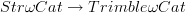    • CommentRowNumber5.
    • CommentAuthorDavid_Corfield
    • CommentTimeApr 6th 2010

    Is it only Trimble n-categories that lend themselves to a coinductive formulation?

    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeApr 6th 2010
    • (edited Apr 6th 2010)

    I wrote:

    A reasonable guess seems to be...

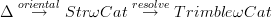    In fact, the strategy that I would see which one might try to follow to prove the homotopy hypothesis for Trimble \omega-categories is to show that the simplicial nerve induced by \Delta \stackrel{oriental}{\to} Str \omega Cat \stackrel{resolve}{\to} Trimble \omega Cat lands in weak complicial sets. For weak complicial sets the homotopy hypothesis is clear. One would expect that the nerve produces even an equivalence of Trimble \omega-categories with weak complicial sets, for instance in that it serves to transfer Dominic Verity's model structure on stratified simplicial sets to Trimble \omega -categories. That would be much more than just the homotopy hypothesis, of course.

    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeApr 6th 2010

    created stub for model structure for weak omega-categories with a query box containing a comment along the above lines

    • CommentRowNumber8.
    • CommentAuthorTodd_Trimble
    • CommentTimeApr 6th 2010

    Thank you, Urs. I'll have to think about this and how it ties up with past thinking on the subject. It feels to me that this basic strategy might apply to any Batanin-like theory of n-categories (the Trimble theory being a special case, i.e., governed by a particular contractible globular operad).

    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeApr 6th 2010
    • (edited Apr 6th 2010)

    It feels to me that this basic strategy might apply to any Batanin-like theory of n-categories (the Trimble theory being a special case, i.e., governed by a particular contractible globular operad).

    Yes.

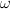    Could you remind me: do you have a natural candidate for how to "puff up" a strict \omega-category to an equivalent Trimble \omega-category which is such that morphisms out of the latter behave like weak morphisms out of the former? I seem to remember you once mentioned something along these lines, but I forget the details.

    • CommentRowNumber10.
    • CommentAuthorUrs
    • CommentTimeApr 6th 2010

    by the way: there is of course a very general theory of model structures on algebras over topological operads. People around me use this to define model stuctures on weak oo-categories conceived as algebras over certain dendroidal sets. But I haven't looked into the details of that yet.

    • CommentRowNumber11.
    • CommentAuthorTodd_Trimble
    • CommentTimeApr 6th 2010

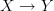    What you may be half-remembering is a proposal for defining weak maps of Trimble \omega-categories X \to Y, as strict maps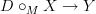

    D \circ_M X \to Y

    where D is a universal contractible bimodule over the globular operad 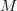M for which 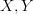X, Y are algebras. (This would also apply generally to Batanin operads, and for all I know Batanin may have something similar in mind). The 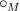\circ_M is a substitution product over 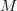M, defined from ordinary substitution by a suitable easy-to-guess reflexive coequalizer.

    I haven't thought much about your specific question, but I'm guessing it isn't very hard.

    • CommentRowNumber12.
    • CommentAuthorTodd_Trimble
    • CommentTimeApr 6th 2010

    @David: I wonder particularly whether coinduction could be applied to the Baez-Dolan case of opetopic sets, particular toward the tricky interlocking conditions on filling in cells (note that in their case too, they defined n-categories only for finite n). Not sure...

    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeApr 6th 2010
    • (edited Apr 6th 2010)

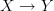    What you may be half-remembering is a proposal for defining weak maps of Trimble \omega-categories X \to Y, as strict maps D \circ_M X \to Y

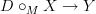
    Yes, thanks. I have your email on this here, but felt too busy to dig it out. Sorry.

    So if you are pretty certain that this 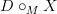D \circ_M X is a good resolution of X in that in fact strict morphisms out of it model all the weak morphisms out of X that one expects, then I am pretty sure that it ought to turn out to be true that

    • the nerve on Trimble 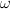\omega-categories induced from 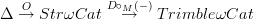\Delta \stackrel{O}{\to} Str \omega Cat \stackrel{D \circ_M (-)}{\to} Trimble \omega Cat naturally factors through weak complicial sets such that it sends Trimble 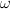\omega-groupoids to Kan complexes.

    And I'd be very interested in seeing if this allows to transfer the model structure for weak complicial sets to Trimble \omega-categories. There are some straightforward things to check to figure this out, though answering some of the checks might be hard.

    At least this is a very explicit strategy for going about the problem.

    • CommentRowNumber14.
    • CommentAuthorMike Shulman
    • CommentTimeApr 6th 2010

    I think Peter Lumsdaine and Steve Awodey have been thinking about this sort of nerve-realization adjunction for Batanin \omega-categories, but with the goal of relating Batanin (\infty,1)-categories to quasicategories (which should then specialize to the groupoidal case too). 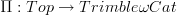I'm a little surprised that it is what you thought of first in the Trimblean case, though, because the operad used there is specifically adapted to topological spaces, not simplicial sets, and we have a naturally defined fundamental \omega-groupoid functor \Pi:Top \to Trimble\omega Cat that doesn't factor naturally through simplicial sets. So I would be more inclined to look for a left adjoint to that. But I guess if we could do the more general Batanin case, then the Trimble case would also follow.

    Urs, could we call that page instead model structure for weak complicial sets? The current title seems overly broad to me. In fact, it's not clear to me that a WCS is really a model for a weak \omega-category, but rather for a weak \omega-category equipped with a subcategory of equivalences containing all its coherences. In particular, if the subcategory contains only identities, then a WCS is exactly a strict complicial set, i.e. a strict \omega-category. The "weak \omega-categories" should be those WCS satisfying an extra "saturation" condition that "everything which acts like an equivalence is an equivalence."

    I believe that Makkai's version of the universality conditions for an opetopic/multitopic n-category can "do \omega" and is essentially coinductive. But I've never looked at it carefully.

    Todd, I gather from #11 that Trimble \omega-categories can be identified with algebras over some Batanin operad? That makes sense, but I haven't seen it written down; can you just take the limit of the operads corresponding to n-categories for finite n?

    I was also thinking recently about whether the coinductive definition of Trimble \omega-categories could be improved to get rid of the partial strictness. It seems to me that if we could give a parallel coinductive definition of weak functors between these things, in such a way that the weak functors form an ordinary 1-category containing the strict functors, then we could just require the operad to act via weak maps rather than strict ones. Do you think the definition of weak functors you mentioned above could be given in such a way?

    • CommentRowNumber15.
    • CommentAuthorUrs
    • CommentTimeApr 6th 2010
    • (edited Apr 6th 2010)

    I think Peter Lumsdaine and Steve Awodey have been thinking about this sort of nerve-realization adjunction for Batanin \omega-categories, but with the goal of relating Batanin (\infty,1)-categories to quasicategories (which should then specialize to the groupoidal case too).

    I didn't know that. Do you have a reference? Not that I have time to read this, but we should link to it somewhere usefully on the nLab.

    I'm a little surprised that it is what you thought of first in the Trimblean case, though, because the operad used there is specifically adapted to topological spaces,

    Maybe a realization directly to 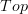Top is more naturally achieved, I don't know. Whatever works will be fine with me. But on the other hand that cosimplicial Trimble omega-category of resolved orientals look like a pretty natural thing to consider, too.

    Urs, could we call that page instead model structure for weak complicial sets? The current title seems overly broad to me

    Right, I have changed it now.

    The "weak \omega-categories" should be those WCS satisfying an extra "saturation" condition that "everything which acts like an equivalence is an equivalence."

    You mean a weak complicial set will not be weakly equivalent to itself with the saturated stratification?

    • CommentRowNumber16.
    • CommentAuthorMike Shulman
    • CommentTimeApr 6th 2010

    Do you have a reference?

    I said thinking about, not writing about. (-: I don't know what sort of results they might have by now.

    You mean a weak complicial set will not be weakly equivalent to itself with the saturated stratification?

    I don't know why it would be. I don't even see a naturally defined map in the other direction, since maps of stratified simplicial sets must preserve the stratification.

    • CommentRowNumber17.
    • CommentAuthorTodd_Trimble
    • CommentTimeApr 7th 2010

    Mike (referring to # 14): I haven't checked this carefully either, but yes, I think it makes sense to take an inverse limit of the "incoherent" globular operads in the category of globular operads, and I guess this inverse limit is exactly the globular operad whose algebras are Trimble \omega-categories. I should check this out when I have some more time.

    I'm not sure about coinduction applied to define weak \omega-functors. Regarding a 1-category of weak maps: I had begun to write some notes on my web (Further developments on Trimble n-categories) which were to lead up to a universal contractible bimodule D over any contractible operad M (these were ordinary operads, but the development should be carried out for globular operads, now that I think of it). 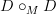The idea I had, if it indeed works, is that D \circ_M D should also be a contractible bimodule, so that by universality we have a coassociative comultiplication 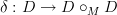\delta: D \to D \circ_M D. This would allow one to compose strict M-algebra maps

    D \circ_M X \to Y \qquad D \circ_M Y \to Z

    to get a strict M-algebra map 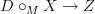D \circ_M X \to Z. Under this, weak maps would compose associatively.

    It would, by the way, come as a big psychological relief to me to get rid of the partial strictness.

    • CommentRowNumber18.
    • CommentAuthorMike Shulman
    • CommentTimeApr 7th 2010

    Interesting idea, Todd. That seems possible, and similar to some of the things I was thinking about, although I was thinking in terms of multicategories with two objects rather than operads -- those seem like the "collages" of bimodules between operads. I would like to read whatever you have to say about the definition/construction of D, if anything.

    • CommentRowNumber19.
    • CommentAuthorUrs
    • CommentTimeApr 7th 2010

    It would, by the way, come as a big psychological relief to me to get rid of the partial strictness.

    One might pass to the full subcategory of Trimble omega-categories of the form 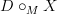D \circ_M X for some Trimble omega-category X. In there no further tricks have to be played to make all morphisms be weak omega-functors.

    • CommentRowNumber20.
    • CommentAuthorDavidRoberts
    • CommentTimeApr 7th 2010

    @Urs,

    I'm sure you've got this in mind, but compare with the category of 2-categories and weak 2-functors as ana-2-functors built from strict 2-functors. This formally makes sense, but seems weird to me, because all 2-categories that arise as the fibrant (cofibrant? can't remember which) replacement of a given 2-category are rather large, one can't talk about small (in the non-technical sense) ones. In particular, the Trimble omega-groupoid naturally associated to a space (the one we all know the fundamental globular oo-groupoid to be) has to be put through a wringer to get out one of the form you suggest.

    • CommentRowNumber21.
    • CommentAuthorUrs
    • CommentTimeApr 7th 2010

    because all 2-categories that arise as the fibrant (cofibrant? can't remember which) replacement of a given 2-category are rather large,

    That's right. The cofibrant 2-categories are enlarged to such a degree that all possible compositors that a weak functor might introduce are already present as 2-morphisms, so that strict functors are already the same as weak 2-functors.

    In particular, the Trimble omega-groupoid naturally associated to a space (the one we all know the fundamental globular oo-groupoid to be) has to be put through a wringer to get out one of the form you suggest.

    Right. And as always, there are two ways to go about this:

    • for general abstract reasoning we don't care if any given object you happen to be able to write down is replaced by an equivalent one, which may be harder to write down. After all, they are equivalent.

    • for concrete computations, we may want to keep the concrete given object and manipulate that, instead of feeding it through a general abstract replacement machinery. This we can also do, but then we have to take as morphisms not the simply-defined morphisms, but ana-morphisms, i.e. suitable spans.

    It's a trade-off. But the oo-category theory will hide somewhere, either in the structure of the objects, or of the morphisms. And it's a very general pattern: either we pass to a subcategory of sufficiently resolved objects or we retain the bigger category of all objects but then have to take care to replace when we hom between them.

    You may like this state of affairs or not. But it is unlikely to be up to debate. That's the way higher category theory works.

    • CommentRowNumber22.
    • CommentAuthorMike Shulman
    • CommentTimeApr 7th 2010
    • (edited Apr 7th 2010)

    The problem of partial strictness is not just in getting the right maps once we have the objects defined, but in getting the right objects. The point is that the fact that inductive (or coinductive) definition of Trimble n-categories uses strict morphisms of Trimble (n-1)-categories in defining the operad action. In particular, that makes the interchange law hold more strictly than you might like. And since the domain of the operad action is a product of categories, even if each of those categories is cofibrant, it's not clear that their product will be -- for 2-categories already the cartesian product does not preserve cofibrant objects. So I think we need either a good notion of weak morphism which composes associatively, or a "Gray tensor product" which preserves cofibrant objects. The former seems closer in reach to me at the moment.

    Of course, what we're really looking for is some sort of cofibrant replacement comonad, in order to make the weak maps compose associatively. I think morally that's what Todd's 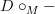D\circ_M - is. Another way to get such a comonad would be Garner's, but that is less explicit, although it would probably work.

    • CommentRowNumber23.
    • CommentAuthorMike Shulman
    • CommentTimeApr 7th 2010

    And Urs, I don't think the situation is as cut-and-dried as all that. For one thing, the situation you describe is only true in algebraic models: with quasicategories, for instance, everything is cofibrant, so we don't need to replace anything before mapping out of it. Of course there we have the dual problem that not all simplicial sets are fibrant, but to my mind that at least a different problem, which manifests itself in different ways.

    Also, I don't see any a priori reason why some algebraic notion of higher category may not admit a well-behaved, intrinsically defined, notion of "weak functor" that doesn't involve explicitly passing to a cofibrant replacement. We work with bicategories and pseudo 2-functors all the time, for instance, without ever worrying about the fact that we could, if we wanted to, construct pseudo 2-functors by considering strict 2-functors out of a cofibrant replacement. The model structure, if there is one, will only live on the category of strict morphisms, but if everything is defined intrinsically enough, a model structure might not be necessary for day-to-day use of the theory.

    • CommentRowNumber24.
    • CommentAuthorUrs
    • CommentTimeApr 7th 2010

    Mike,

    sure, nothing here that I disagree with.

    Of course there is no law that says that all notions of weak morphisms of higher categories have a model in terms of "simple maps" out of something like cofibrant into something like fibrant objects. But it seems to be the case in all examples we know of.

    By the way, in the operadic definition of oo-categories pursued here in Utrecht, where one considers algebras over a resolution of the Assoc-operad on a given set of objects and then takes the colimit over all possible sets of objects, there is also a certain strictness induced, namely strict composition of 1-morphisms. While a proof is not yet available, the general conviction is that this is no problem, but a case of the semi-strict infinity-category-phenomenon: every oo-category should be equivalent to one of this form.

    • CommentRowNumber25.
    • CommentAuthorTodd_Trimble
    • CommentTimeApr 7th 2010

    Thanks for that reference to Garner's paper, Mike. I am clearly behind the times.

    Probably the comonad he writes down would be exactly suitable for my purposes, but I'd have to read and think about it more.

    Something he wrote caught my eye: that the substitution tensor product on globular collections does not preserve reflexive coequalizers in the separate arguments (which would be needed to get a bicategory of operads, bimodules, and bimodule homomorphisms). I guess I was sort of hoping it would (in the case of substitution product on graded sets, it does). I guess the problem is that the functor X \mapsto X^{[T]}, where [T] is the underlying globular set of a Batanin tree, need not preserve reflexive coequalizers.

    • CommentRowNumber26.
    • CommentAuthorDavidRoberts
    • CommentTimeApr 8th 2010

    Urs wrote:

    You may like this state of affairs or not. But it is unlikely to be up to debate.

    Not that I do or don't like it, I just find a little strange :) Like I said, I understand exactly why you'd want to do this, and why it should in principle work. Perhaps it is this sort of dissatisfaction that makes me work with the concrete techniques that I do (e.g. homotopy groups of topological groupoids, as a proxy for the abstract nonsense version of such for topological stacks).

1 to 26 of 26

  1.