nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeApr 6th 2010
- (edited Apr 6th 2010)
expanded the previously pretty empty entry smooth Lorentzian space.
I added some standard definitions for smooth Lorentzian manifolds and then a discussion on how a time orientation without closed future-directed curves induces the structure of a category that is a poset, where a morphism
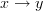 witnesses the fact that
witnesses the fact that 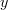 is a point in the future of
is a point in the future of  .
. -
- CommentRowNumber2.
- CommentAuthorEric
- CommentTimeApr 6th 2010
- (edited Apr 6th 2010)
<p>I wish Sorkin would see this and get involved :)</p> <p>I always enjoyed his ideas and, if I were smarter, would trying to nPOV them (if I can use nPOV as a verb :))</p> <p>Edit: My my. It has been a while since I looked up Sorkin and look what I found:</p> <p><a href="http://www.google.com.hk/url?sa=t&source=web&ct=res&cd=10&ved=0CDgQFjAJ&url=http%3A%2F%2Fciteseerx.ist.psu.edu%2Fviewdoc%2Fdownload%3Fdoi%3D10.1.1.101.8551%26rep%3Drep1%26type%3Dpdf&rct=j&q=Sorkin+poset&ei=TUW7S8SPDYuC7QOpvIHlBQ&usg=AFQjCNG7xMT3TeyaQ5GQHak5XYcnZSnATA&sig2=tyTclGng8stP1GiMdz6NEg">A Spatial View of Information</a><br> Jonathan Gratus and Timothy Porter</p> <p>Here Tim has been doing all kinds of fascinating stuff all along and I didn't even know it :)</p> -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeApr 6th 2010
all kinds of fascinating stuff
Let's link to this somewhere on the nLab with a brief comment on what it is about and where it fits, so that I can find it next time that I have a minute...
-
- CommentRowNumber4.
- CommentAuthorTim_van_Beek
- CommentTimeApr 6th 2010
Hi,
I tried to add a little bit about different notions of causality, hoping that I did not mess up what you had in mind for the page... -
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeApr 6th 2010
- (edited Apr 6th 2010)
Thanks, Tim! Very nice.
I just went through it again and polished slightly here and there.
Among other things I made the Wikipedia links you gave channel through stub nLab entries Anti de Sitter space and Kerr spacetime.
I feel we should generally do this, because otherwise later on when we do create our own nLab entries that may crucially differ from Wikipedia material (not so likely in this case here, but still) we would have to try to chase all previous links to Wikipedia and redirect them back to our own wiki. Of course the nLab page of the same title may and should link to Wikipedia!
Thanks for mentioning the point of ergodic causality. Do you happen to know any results on perturbations of exact solutions? I would imagine for instance that while the Kerr solution itself is not chronological, small perturbations of it will tend to make it chronological (by turning all closed timelike cruves into just ergodic timelike curves).
This might be relevant in view of the nice category-theoretic interpretation of causalness = poset. I am not sure if global hyperbolicity has an equally relevant categorical interpretation. On the other hand, possibly that's quite besides the point... :-)
-
- CommentRowNumber6.
- CommentAuthorEric
- CommentTimeApr 6th 2010
Cool :)
-
- CommentRowNumber7.
- CommentAuthorIan_Durham
- CommentTimeApr 6th 2010
As I noted in Urs' forum post on 'spacetime,' I really see no need for spacetime to have its own entry, at least based on what Urs has put in that stub. Everything I would want in an entry on spacetime is already in the smooth Lorentzian manifold entry. So I question the need for a separate entry.
Incidentally, it would be nice to coax John Baez into getting back into posting things since he's done some work on categories and quantum gravity (for instance, see this article). -
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeApr 6th 2010
I added Penrose/Rindler reference.
-
- CommentRowNumber9.
- CommentAuthorTim_van_Beek
- CommentTimeApr 7th 2010
Urs said:
" I made the Wikipedia links you gave channel through stub nLab entries Anti de Sitter space and Kerr spacetime. I feel we should generally do this..."
Ok, no problem, I will try to keep that in mind.
Do you happen to know any results on perturbations of exact solutions?
No, but if I come across one, I will try to remember to mention it on the nLab somewhere.
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeApr 7th 2010
- (edited Apr 7th 2010)
I added a section that describes the (2,1)-category of paths in a smooth Lorentzian space. at Path n-category of a smooth Lorentzian space. Nothing deep there, but the concept might be of interest.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeJul 14th 2020
added pointer to
- Leandro A. Lichtenfelz, Paolo Piccione, Abdelghani Zeghib, On the Isometry Group of Lorentz Manifolds, in: Miguel Sanchez, Miguel Ortega, Alfonso Romero (eds.) Recent Trends in Lorentzian Geometry, Springer 2013 (doi:10.1007/978-1-4614-4897-6_12)
for discussion of Lorentzian structure as G-structure
1 to 11 of 11