nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorHarry Gindi
- CommentTimeMay 22nd 2010
- (edited May 22nd 2010)
I think we should adopt one convention and stick to it. I realize that in principle, writing C(X,Y) and D(X,Y) is better notation for the hom-sets in categories C and D, but in practice, I (and it seems the majority of the people here) use the notation Hom_C and Hom_D.
If I have a vote, I vote for the Hom notation because it makes it much easier to follow what’s going on if you’re skimming for something specific. If you don’t follow the introduction of the categories C and D, it’s not always clear what is a category. The Hom notation, while more verbose, makes it clear exactly what is going on.
I only ask because it’s actually really quite painful to keep switching back and forth between the two notations while reading articles on the lab.
It seems like there was a lot of support for the C(X,Y) notation a while back, but it’s lost ground recently and is doesn’t really appear too much in more recent articles.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeMay 22nd 2010
Personally, I have this convention:
I write to indicate an un-enriched hom, and to denote an enriched hom, if any.
The distinction often matters. For instance the definition of the enriched Hom of, say, simplicial sets is
This follows pretty established conventions in enriched category theory literature (though there is no universally accepted convention).
Of course when we are just talking about locally small categories, then both notations do coincide. I think I tend to write then in more elementary discussion and if the emphasis is more on doing some real work.
-
- CommentRowNumber3.
- CommentAuthorHarry Gindi
- CommentTimeMay 22nd 2010
- (edited May 22nd 2010)
I propose the following awesome notation:
Classical remains for the standard (and very classy) Hom bifunctor from the definition of a category.
Maybe something like denotes the enriched hom.
In all seriousness, the notation C(-,-) makes things look like a giant jumble of letters, which does nothing but obscure the point. I was trying to read the definitions over at weighted colimit, and it was a painful ordeal using the letter-only notation. I’m going with Grothendieck and Bourbaki on this one.
-
- CommentRowNumber4.
- CommentAuthorMike Shulman
- CommentTimeMay 22nd 2010
I don’t see why we need a single convention. We use varying conventions for lots of things. I’ve been forced to get used to the “Hom” notation which I usually find redundant and cumbersome, so why don’t you also get used to the simpler notation, Harry? I find that it is fairly universally used among category theorists. The established convention in enriched category theory that I have seen everywhere is to write for the enriched hom and for the underlying unenriched hom, since is the enriched category and denotes the underlying ordinary category.
-
- CommentRowNumber5.
- CommentAuthorHarry Gindi
- CommentTimeMay 22nd 2010
- (edited May 22nd 2010)
In my experience,
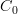 is standard for
is standard for 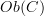 , and
, and 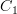 is standard for
is standard for 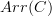 (this is also on the lab in some places).
(this is also on the lab in some places).Edit: I made a mistake and will fix it in a subsequent edit.
Edit 2: Alright, here's the problem with the C(-,-) notation: It's great until you bring functors into the mix. C(x,y), nice, looks great! But wait, what about
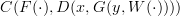 ? It looks like a bunch of letters all mishmoshed together. Here is what that reads with homs:
? It looks like a bunch of letters all mishmoshed together. Here is what that reads with homs: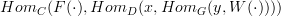
It's longer to type, no doubt, but it's substantially more readable.
-
- CommentRowNumber6.
- CommentAuthorHarry Gindi
- CommentTimeMay 22nd 2010
Also, functor categories. , or [C^{op},Set]? I prefer the latter, to be honest.
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeMay 22nd 2010
For functor categories, as before, I tend to write if I want to emphasize that this might be an enriched functor category, as for these it is the standard notation.
So again the difference does not matter much for locally small categories, but does matter as soon as an enrichment is around.
-
- CommentRowNumber8.
- CommentAuthorHarry Gindi
- CommentTimeMay 22nd 2010
Well, I feel like we should have global conventions on this thing, especially if you're implicitly using it to denote enrichment.
-
- CommentRowNumber9.
- CommentAuthorTodd_Trimble
- CommentTimeMay 22nd 2010
I agree with Mike # 4 – I have used many different conventions in my life, and would not be comfortable having to stick to the same one always. I’d be even less comfortable telling writers which conventions they should use.
A ’pro’ of using the notation for homs is ease of fit into diagrams, and less redundancy. A ’con’ is that not everyone is familiar with the notation (but that’s easily addressed by saying “let be the set of morphisms…”). From a visual standpoint, sometimes it’s nice to have the trim, compact , and sometimes it’s nice to have the more spread-out .
Personally, I like using lower-case for hom-sets, and for internal homs. You can even have a mix of notations: use for enriched homs, so that you can define the underlying ordinary category of an enriched category by the formula .
I’ve used both and , and I’ve used both and . Again, each convention has advantages and disadvantages, and sometimes moods and intuitions to go with it.
But as a writer, one should have the freedom to choose whatever feels right for the occasion.
-
- CommentRowNumber10.
- CommentAuthorEric
- CommentTimeMay 22nd 2010
- (edited May 22nd 2010)
Content is more important than notation. Getting agreement would be impossible. Best just to add content the best you can. Chances are someone will come along and change your notation anyway, so there is not much use fretting over it, e.g. if you want to use (or whatever), go for it, but you probably will not convince others to change.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeMay 22nd 2010
- (edited May 22nd 2010)
I agree, common convention is impossible to achieve. But maybe it doesn’t hurt to discuss this a bit, because we might all be converging to something anyway.
For instance I feel very much inclined to all of what Todd says in #9.
The only observation I have is that it seems to me (but I may be wrong, I haven’t done a syetematic literature survey) that the capitalization is usually used the other way round: don’t most people introduce the Hom-set with capital symbols and then later on define the internal one with lower case? Well, actually many people like to write the internal hom as in lower case and underlined. In any case I feel that writing the internal hom has just risks some misunderstanding.
Kelly systematically uses [-,-] for internal hom. I like that choice.
-
- CommentRowNumber12.
- CommentAuthorTodd_Trimble
- CommentTimeMay 22nd 2010
Regarding what Urs said
The only observation I have is that it seems to me (but I may be wrong, I haven’t done a syetematic literature survey) that the capitalization is usually used the other way round: don’t most people introduce the Hom-set with capital symbols and then later on define the internal one with lower case? Well, actually many people like to write the internal hom as in lower case and underlined. In any case I feel that writing the internal hom as just Hom risks some misunderstanding.
You may be right about which is more usual; I’m not sure. I’ve never understood the logic of that: to me, “Hom” looks like “hom” with more ’oomph’ to it, so “hom” looks like it should be for bare-bones sets and Hom for something more enriched. Be that as it may, I would grudgingly go along if the usual convention is what Urs says it is.
As a general rule, I’m nervous about people deciding what notation is best for us. Harry seems to have very decided opinions about this and seems about to make a bunch of changes to suit his fancy over at operad. For us at the nLab, I would instead counsel notational tolerance, because opinions are divided and highly subjective. The main thing is to make sure the sense is clear.
-
- CommentRowNumber13.
- CommentAuthorEric
- CommentTimeMay 22nd 2010
Relax and have a nice day. When all is said and done, there is always the “Rollback” button :)
-
- CommentRowNumber14.
- CommentAuthorMike Shulman
- CommentTimeMay 23rd 2010
For us at the nLab, I would instead counsel notational tolerance, because opinions are divided and highly subjective.
Hear hear. In general I think the rule should be to maintain consistency within each page whenever possible, and have respect for what others have written. That means not just going through and changing all the notation on a page, even if it’s not what you prefer, and also when you add to a page you should try to maintain the same notation used in the rest of it.
-
- CommentRowNumber15.
- CommentAuthorHarry Gindi
- CommentTimeMay 23rd 2010
In general I think the rule should be to maintain consistency within each page whenever possible, and have respect for what others have written.
Then if a single page is using two different conventions, I can pick the one I like better and change the rest of them?
-
- CommentRowNumber16.
- CommentAuthorTodd_Trimble
- CommentTimeMay 23rd 2010
As a matter of fact, I feel this tolerance (in the strong sense Mike just enunciated, which goes beyond mere tolerance to include respect and consideration) should be discussed as general advice to the would-be contributor.
I mean, we could also have rollback wars and endless bickering such as one finds on the discussion pages of Wikipedia, but that can quickly become aggravating and time-consuming. Note that all this is a matter of personal ethics; nobody is telling another they have to conform to what they see on a page when they edit it, but it does makes a lot of sense to be courteous when editing.
-
- CommentRowNumber17.
- CommentAuthorHarry Gindi
- CommentTimeMay 23rd 2010
Proposal:
Unenriched hom:
Enriched Hom:
Internal Hom:
Functor Category:
With the following further convention: If you are working on a page where enrichment doesn’t appear, you may also use for the unenriched hom, and if no internal categories are involved, is okay for the functor category.
There may be slight complications in cases where there is a homotopy category (say C is SSet-enriched), then [X,Y] denotes the hom in the homotopy category, which forces us to use the notation. This seems like a flexible enough convention and is consistent with the books I’ve read.
-
- CommentRowNumber18.
- CommentAuthorMike Shulman
- CommentTimeMay 23rd 2010
if a single page is using two different conventions, I can pick the one I like better and change the rest of them?
Hmm, I’m not sure. That could amount to a sanction of someone else’s disrespect for the original author’s conventions.
Proposal:
I’m not going to agree to any single proposal. But it might be useful to have lists of all the extant notations at places like hom-set and enriched category and functor category.
-
- CommentRowNumber19.
- CommentAuthorEric
- CommentTimeMay 23rd 2010
I’m not going to agree to any single proposal. But it might be useful to have lists of all the extant notations at places like hom-set and enriched category and functor category.
Or even Notation
-
- CommentRowNumber20.
- CommentAuthorTodd_Trimble
- CommentTimeMay 23rd 2010
Regarding Mike’s response at #18:
That could amount to a sanction of someone else’s disrespect for the original author’s conventions.
It could also be that in the middle of an edit, someone inadvertently forgot the original author’s conventions because he/she was concentrating on the math. Then there’s a single variance in convention, and a third person thinks, “Aha, here’s my chance!” and then changes the whole page to match the variant convention.
Something about this attitude doesn’t exactly evince comity or esprit de corps.
-
- CommentRowNumber21.
- CommentAuthorTobyBartels
- CommentTimeMay 23rd 2010
But on the other hand, if the third party doesn’t know the history, then you can’t blame them. And I would include not bothering to check the history as OK. The important thing is not to stick with the original for all time, but to not get into fights about it.
My own policy (which I began on Wikipedia) is to stick with the notational choices on the page unless I find myself (for independent reasons) rewriting significant amounts. Then I can use my preferred notation (which I would naturally use when writing my new material) and change the rest to match. And if there’s already inconsistency, them I can choose either (or scrap them both and substitute mine), as long as both styles are well represented (so a single slip or typo doesn’t open the door).
One could (as a personal policy, not an nLab rule) make this more formal. Sort of a law of majority rule, where the voting is done by whatever’s already on the page. But when you write new stuff, you write it first (in your own notation), then count the vote.
-
- CommentRowNumber22.
- CommentAuthorAndrew Stacey
- CommentTimeMay 23rd 2010
I’m opposed to deciding on a convention to use. The thing to remember is that the nLab is intended to be useful to someone recording their research at that moment in time. So if I have to keep remembering “do I write homs as this or that?” it’s going to become annoying for me to make notes on whatever I’m making notes on. A particularly pertinent case is making notes on a paper, initially, one is going to want to use the notation of the paper.
So any “guidelines for editors/authors” needs to take this into account: if it is designed to help the contributor at the moment of contributing then it is useful, but if it hinders the contributor then it is not useful. So Urs’ recent urging to have some structure on pages is at worst neutral, but at best helpful since having some structure on a page helps me be structured in my thoughts. Similarly, with making wikilinks to everything, that at worst is neutral since putting square brackets doesn’t take up any time or thought, but at best helpful since I can see what is already on the lab elsewhere. But remembering hom-set notation is at best neutral and at worst a hindrance so I don’t want to have such a convention.
However, here’s where the second person in can help. If, when reading through a page, you find that the hom-set notation (for example) is confusing, you can add clarification.
But note the word “add”. It is important to be respectful of others’ contributions. A major change as in changing all the hom-set notation on a page should probably be discussed here first. But what I would deem as perfectly acceptable would be clarifying remarks. So one could say at the top,
“The convention on this page is to use … notation. Occasionally, that can get unwieldy and it can be helpful to rewrite some of the expressions in the alternative … notation. For the precise dictionary between the two, see the page Notation.”
Then, when there’s an expression that is tricky to understand, simply at a sentence, “In the … notation, this looks like … from which we can easily see that … and … and … are true.”.
-
- CommentRowNumber23.
- CommentAuthorTobyBartels
- CommentTimeMay 23rd 2010
Although I also don’t want to fix conventions for things like hom-sets which have many overlapping notations, it is also possible to set a convention for lab elves that new contributions are not required to meet. Such a convention is neutral for new contributions, since those can ignore the convention; it just means that lab elves may come along later and change it.
1 to 23 of 23