Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nforum nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: Whitehead tower

Bottom of Page

1 to 19 of 19

  1.  
    • CommentRowNumber1.
    • CommentAuthorGuest
    • CommentTimeOct 13th 2009
    started Whitehead tower, plus some speculative comments on versions using higher categories.

    -David Roberts
    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeOct 13th 2009

    Thanks, David!

    I added a bit to the section on "Constructions" by co-killing of homotopy groups (properly speaking it should be "co-killing" for the Whitehead tower where it is "killing" for the Postnikov tower).

    I'd be interested to see more details on your construction that you mention. I suppose I should look through your thesis.

    But I am wondering about this: the Whitehead tower construction really works in every (oo,1)-topos: there is a notion of homotopy groups of any object in an (oo,1)-topos (but currently the only entry we have is n-truncated object of an (infinity,1)-topos). Lurie discusses Postnikov towers in HTT.

    What you mention sounds like it wants to become the Whitehead tower construction in something like the (oo,1)-topos of oo-stacks on Top. Could that be?

    Notice that Dugger has the nice result, mentioned at homotopy localization, that homotopy invariant oo-stacks on Top are equivalent to topological spaces. That reminds me a bit of the remarks you made, where you approach the Whitehead construction in Top but using topological groupoids. Maybe I am wrong, i haven't really looked at your construction closely. (You should provide a direct link to page and verse to the page on Whitehead tower.)

    • CommentRowNumber3.
    • CommentAuthorGuest
    • CommentTimeOct 14th 2009
    As my thesis is not quite finished I felt like being a bit secretive as to my general idea. But since we are all friends here, I'll put a bit in when I have some time.

    A question about the n-truncated objects: is that fairly straightforward? For classical $Top$ the whole thing is a mess: killing homotopy groups - and I mean killing, not co-killing - by representatives of generators of homotopy groups. If one passes to simplicial (pre)sheaves on Top, which would be the ultimate sensible thing to do if I pursue this particular thought, then it's ok. How about other $(\infty,1)$-topoi?

    -David Roberts
    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeOct 14th 2009
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote> As my thesis is not quite finished I felt like being a bit secretive as to my general idea. </blockquote> <p>Oh, I see. to clarify: all I meant to indicate is: what you say sounds interesting, I wish I knew where to learn abnout it in more detail!</p> <blockquote> A question about the <img src="/extensions/vLaTeX/cache/latex_485d65c1e6e7757e4de10eb91bc9382b.png" title="n" style="vertical-align: -20%;" class="tex" alt="n"/>-truncated objects: is that fairly straightforward? For classical <img src="/extensions/vLaTeX/cache/latex_d135fddf839f5858264c53bd39d0a7fc.png" title="Top" style="vertical-align: -20%;" class="tex" alt="Top"/> the whole thing is a mess: killing homotopy groups - and I mean killing, not co-killing - by representatives of generators of homotopy groups. If one passes to simplicial (pre)sheaves on Top, which would be the ultimate sensible thing to do if I pursue this particular thought, then it's ok. How about other <img src="/extensions/vLaTeX/cache/latex_5b4e8bf1a57dcb0e372c2512e8f20c01.png" title="(\infty,1)" style="vertical-align: -20%;" class="tex" alt="(\infty,1)"/>-topoi? </blockquote> <p>I will write entries now on truncation, truncated objects and Postnikov towers in <img src="/extensions/vLaTeX/cache/latex_5b4e8bf1a57dcb0e372c2512e8f20c01.png" title="(\infty,1)" style="vertical-align: -20%;" class="tex" alt="(\infty,1)"/>-toposes, summarizing Lurie's material.</p> <p>The general theory is rather nice and satisfactory. I suppose the mess that you are thinking of is one of actual constructions of n-truncations?</p> <p>i would like to simply "dualize" Lurie's discussion of Postnikov towers of oo-stacks to one of Whitehead towers. It feels like it should be obvious enough, but I am not nevertheless not exactly sure how to precisely state the condition of the universaility that the morphisms in the tower have to satisfy. It must have an easy answer, but I may need to think about it more...</p> <p>(by the way David: the dollar-sign latex seems to be broken here: what does work is including stuff in and html-like "latex" tag.)</p> </div>
    • CommentRowNumber5.
    • CommentAuthorTobyBartels
    • CommentTimeOct 14th 2009

    what does work is including stuff in and html-like "latex" tag

    You can also use double dollars (which will still be inline, not displayed), which is easier to type but will not work in the preview.

    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeOct 14th 2009

    hm, last time I tried double dollars didn't work either. Okay, new attempt:

    \exp(2 \pi i) - 1 = 0
    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeOct 14th 2009

    What do you all see? I see a "formula does not parse" error.

    but let me try this

    1
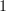
    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeOct 14th 2009

    ah, then let me try this:

    \exp(2 \pi i) - 1 = 0
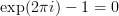
    • CommentRowNumber9.
    • CommentAuthorUrs
    • CommentTimeOct 14th 2009

    Okay, that explains it. The double dollars and the content they bracket have to be on the same line!

    With double dollars I am genetically programmed to have line breaks after the initial and before the closing one. That explains my baad luck with them here...

    • CommentRowNumber10.
    • CommentAuthorTobyBartels
    • CommentTimeOct 15th 2009

    On the subject of the Whitehead tower, I normalised the list of groups in the tower of \mathrm{O}(n) in their various articles: Fivebrane group to string group to spin group to special orthogonal group to orthogonal group. Out of curiosity, why is that first one always capitalised?

    • CommentRowNumber11.
    • CommentAuthorUrs
    • CommentTimeOct 15th 2009
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote> Out of curiosity, why is that first one always capitalised? </blockquote> <p>Er, that might just be my German capitalization instinct ;-)</p> <p>Probably it shouldn't be. In fact Ithink 90 per cent of the time or so I also capitalised <a href="https://ncatlab.org/nlab/show/String+group">String group</a> and <a href="https://ncatlab.org/nlab/show/Spin+group">Spin group</a>.</p> <p>In formulas it's <img src="/extensions/vLaTeX/cache/latex_54bb7afed08351ea1e544d0f360cbe1b.png" title=" Spin(n) " style="vertical-align: -20%;" class="tex" alt=" Spin(n) "/> and <img src="/extensions/vLaTeX/cache/latex_17875b9d51a59d67c41a60b50ee16f69.png" title=" String(n) " style="vertical-align: -20%;" class="tex" alt=" String(n) "/> and <img src="/extensions/vLaTeX/cache/latex_ff1fab2a7c74dcc88e068904c2db49cd.png" title=" Fivebrane(n) " style="vertical-align: -20%;" class="tex" alt=" Fivebrane(n) "/> with capitals. But I gather one doesnt write "Spin group" but "Spin group"? If so, it should probably also be "fivebrane group", too.</p> </div>
    • CommentRowNumber12.
    • CommentAuthorTobyBartels
    • CommentTimeOct 15th 2009

    Er, that might just be my German capitalization instinct ;-)

    No, it's not; it's also in the references. Otherwise I'd have just changed it!

    • CommentRowNumber13.
    • CommentAuthorTobyBartels
    • CommentTimeOct 15th 2009

    Also, you can definitely capitalise at the beginning of a sentence. (^_^)

    • CommentRowNumber14.
    • CommentAuthorTobyBartels
    • CommentTimeOct 15th 2009

    Wait a minute … you wrote those references! So maybe you're right, and you are wrong after all.

    Now if it were me, I'd write ‘5-brane’.

    • CommentRowNumber15.
    • CommentAuthorUrs
    • CommentTimeOct 15th 2009
    This comment is invalid XHTML+MathML+SVG; displaying source. <div> <blockquote> Wait a minute … you wrote those references! </blockquote> <p>hehe. Not alone, though. And not all of (the two of) them.</p> <p>But there was some back and forth after this was accepted with the typesetting editor on such capitalization issues. Tomorrow, when I am more awake, I'll remind myself which convention made it into the published version. I forget.</p> </div>
    • CommentRowNumber16.
    • CommentAuthorGuest
    • CommentTimeOct 15th 2009
    A bit more at Whitehead tower, on the classical construction and analogues for (infinity,1)-cateories. Will get to my version soon, Urs.

    -David Roberts
    • CommentRowNumber17.
    • CommentAuthorGuest
    • CommentTimeOct 15th 2009
    More at Whitehead tower, this time on my own thoughts on how one could fancy the whole thing up the n-categorical ladder.

    In response to a question earlier, the 'mess' I was talking about was the lack of functorial Postnikov towers in Top. They are certainly available in the category of Kan complexes (and by the Ex^oo functor, on sSet, I imagine).
    • CommentRowNumber18.
    • CommentAuthorUrs
    • CommentTimeNov 13th 2009

    added a section "functorial constructions" to Whitehead tower by copying stuff from a MathOverflow discussion

    • CommentRowNumber19.
    • CommentAuthordomenico_fiorenza
    • CommentTimeJan 10th 2010
    • (edited Jan 10th 2010)
    edited Whitehead tower at "Construction by cokilling of homotopy groups"

1 to 19 of 19

  1.