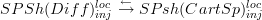nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
nLab > Latest Changes: site-dependence of model structure on simplicial presheaves
Bottom of Page1 to 11 of 11
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeOct 21st 2009
I started a section
dependence on the underlying site at model structure on simplicial presheaves.
So far this quotes a result from Jardine's lectures and then looks a bit at an example.
At that example I would really like to conclude that the Quillen adjunction discussed there is actually a Quillen equivalence. But I have to interrupt now to make a telephone call... :-)
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeOct 22nd 2009
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeOct 22nd 2009
now also added a section good covers with a definition that I think is good and with a proposition that I think is true and useful.
However, it seems at this point of the night I seem to be unable to write down precisely what in my head seems to be the obvious proof. I wrote down something there, but need to get back to it. Maybe I am wrong, but I am not convinced of that as yet ;-)
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeOct 22nd 2009
I think I got it right now.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeOct 22nd 2009
Danny Stevenson kindly wrote in to say that the fact in question
(that every simplicial presheaf that is degreewise a coproduct of representables is cofibrant in alll these model structures)
should be true and should be stated somewhere in Dan Dugger's work.
He indicates a proof which sounds very much along the lines of the proof that I did give.
So I regard this as settled for the time being, removed the green query boxes and just left in an indented remark that for the time being the proof is one I dreamed up which still deserves checking.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeOct 22nd 2009
renamed the section in question fibrant and cofibrant objects and expanded further.
meanwhile Danny Stevenson writes in and points out various even stroger statements from the literature. Will try to include them after lunch...
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeMay 1st 2023
- (edited May 1st 2023)
just a vague thought:
Is there a non-trivial class of small categories (of posets?) such that for any and in the class, the functor of pullback along (i.e. precomposition with) their product projections happens to be a left Quillen functor for the projective model structures on simplicial presheaves over these categories?
[edit: I’d like these categories not to have a terminal object, in general…]
-
- CommentRowNumber8.
- CommentAuthorDmitri Pavlov
- CommentTimeMay 1st 2023
happens to be a left Quillen functor for the projective model structures on simplicial presheaves over these categories?
This is true if and only if the left adjoint functor sends representable presheaves to projectively cofibrant objects. In our case, an object c_1∈C_1 is sent to the presheaf (d_1,d_2)↦C_1(d_1,c_1).
Therefore, the latter presheaf has to be a retract of a coproduct of representables. This is true if C_2 has a terminal object, since in this case the resulting presheaf is representable by (c_1,1). Otherwise it is easy to construct examples when it’s false, so the answer depends on C_2.
-
- CommentRowNumber9.
- CommentAuthorGuest
- CommentTimeMay 2nd 2023
Thanks for the comments.
I came to wonder about this in thinking about how to get the naive formula for an external tensor product to yield a derivable functor on an integral model structure. In some natural contexts I can see that it behaves like a left Quillen functor on an ambient integral model structure except that (or if only) the initial operation of pullback of either factor to the cartesian product of their bases spaces is or were left Quillen wrt the projective model strcuture.
But this fails badly over sites of simplicial groupoids, since here cofibrancy essentially means free actions of the simplicial Kan loop group, and the partially trivial actions obtained by pullback along projections are as far from this as possible. In view of this, last night, I naively came to wonder whether if I’d pull a Thomason-trick and removed all manifest automorphisms by passing to posetal models of homotopy types I could get around this problem. But now I see that this is hopeless.
As another solution to the problem I guess one could pick a “universe” of simplicial group that one cares about, then blow up the point space to (using here that has itself group structure) and blow up any connected homotopy type that one cares about to , thought of as sliced over the blown-up point via the inclusion (using that this is in fact a group homomorphism) and the identity on all the other factors.
This way, every cofibrant object parameterized by the blow-up of is now freely acted on by all (the and hence) the in the universe. Moreover, the product over the blown-up point of the blow-up of with another is now such that pullback to it along either of the two projections amounts to restricting, in the left factor, say, -actions along the inclusions , which does preserve cofibrancy.
-
- CommentRowNumber10.
- CommentAuthorDmitri Pavlov
- CommentTimeMay 2nd 2023
Re #9: But if your goal is to make the external tensor product into a left Quillen bifunctor, then it seems like it is true: the external tensor product of representable sheaves is simply the representable sheaf of the pair, which is cofibrant even though the individual factors and are not.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeMay 2nd 2023
Oh right, that is true. :-)
1 to 11 of 11