nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeOct 22nd 2009
Is there a term for the condition where all closed k-paths of k-morphisms commute?
In a category, when all 1-paths commute, we have a preorder.
In an n-category, when all n-paths commute, we have a ???
-
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeOct 22nd 2009
-
- CommentRowNumber3.
- CommentAuthorEric
- CommentTimeOct 22nd 2009
- (edited Oct 22nd 2009)
Thanks! That is awesome. I think I need a term for a "free n-poset". What do you think? I've been calling this an "n-quiver", but I think an n-quiver is rather a free n-category.
In other words, given a forgetful functor
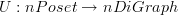
we have a free functor
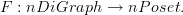
-
- CommentRowNumber4.
- CommentAuthorTobyBartels
- CommentTimeOct 23rd 2009
What do we call the result of
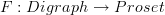 ? Whatever it is, just put an ‘
? Whatever it is, just put an ‘ ’ in front of that!
’ in front of that! -
- CommentRowNumber5.
- CommentAuthorEric
- CommentTimeOct 23rd 2009
- (edited Oct 23rd 2009)
Sounds good to me :) Now we just need to find that name :)
-
- CommentRowNumber6.
- CommentAuthorEric
- CommentTimeOct 23rd 2009
- (edited Oct 23rd 2009)
<div> <p>In the discussion at <a href="https://ncatlab.org/nlab/show/preorder">preorder</a>, we have:</p> <blockquote> John says: You might try to define a <a href="https://ncatlab.org/nlab/show/Hasse+diagram">Hasse diagram</a> to be a <a href="https://ncatlab.org/nlab/show/directed+graph">directed graph</a> whose <a href="https://ncatlab.org/nlab/show/quiver">quiver</a> is a <a href="https://ncatlab.org/nlab/show/poset">poset</a>. In other words, you take a directed graph, consider the free category on that graph, and demand that this category be a poset. However, maybe it’s a rule that a Hasse diagram with directed edges <img src="/extensions/vLaTeX/cache/latex_b6b5cb002712bd65456fa20f4b2ea06f.png" title="x\to y" style="vertical-align: -20%;" class="tex" alt="x\to y"/> and <img src="/extensions/vLaTeX/cache/latex_201816a2d9515e6d446f37d4291b34ea.png" title="y\to z" style="vertical-align: -20%;" class="tex" alt="y\to z"/> is not allowed to have a directed edge <img src="/extensions/vLaTeX/cache/latex_9bb5b774afce97c0c4a429087415f9de.png" title="x\to z" style="vertical-align: -20%;" class="tex" alt="x\to z"/>. If so, this is a further restriction on what directed graphs count as Hasse diagrams. </blockquote> </div> -
- CommentRowNumber7.
- CommentAuthorEric
- CommentTimeOct 23rd 2009
- (edited Oct 23rd 2009)
I'm tentatively defining a Hasse n-graph and maybe the category nHasse.
The n-quiver of a Hasse n-graph (or n-Hasse graph?) is an n-poset.
-
- CommentRowNumber8.
- CommentAuthorEric
- CommentTimeOct 23rd 2009
<div> <p>Hmm... from that same conversation at <a href="https://ncatlab.org/nlab/show/preorder">preorder</a>, I now see that you said:</p> <blockquote>For a Hasse diagram, I like John's definition. It is true that a Hasse diagram shouldn't have an edge <img src="/extensions/vLaTeX/cache/latex_9bb5b774afce97c0c4a429087415f9de.png" title="x\to z" style="vertical-align: -20%;" class="tex" alt="x\to z"/> if there are edges <img src="/extensions/vLaTeX/cache/latex_9b17588d2819cbd839b0a226ac727369.png" title="x\to y\to z" style="vertical-align: -20%;" class="tex" alt="x\to y\to z"/>, but this follows; it's not a further restriction. (Similarly, there can't be any loops, even though directed graphs in general should allow them.)</blockquote> <p>Would you mind explaining that?</p> <p>Isn't the quiver of the "walking square with no diagonal" the same as the quiver of the "walking square with diagonal"?</p> <p>The "walking commutative square" is a 1-poset. There is no graph whose quiver is the walking commutative square though. Is there? But the WCS has a Hasse diagram (being the "walking square with no diagonal"). Every poset has a Hasse diagram.</p> <p>Ok ok. I think I see. Could it be that you cannot define a Hasse diagram to be the graph whose quiver is the poset because some posets are not quivers of some graph?</p> </div> -
- CommentRowNumber9.
- CommentAuthorTobyBartels
- CommentTimeOct 24th 2009
- (edited Oct 24th 2009)
OK, yeah, you are right and John was wrong. (This means that I just made some silly comments on the Lab, so maybe I'll remove them.) The poset
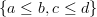 is our counterexample; it is not the quiver of its Hasse diagram.
is our counterexample; it is not the quiver of its Hasse diagram. -
- CommentRowNumber10.
- CommentAuthorTobyBartels
- CommentTimeOct 24th 2009
OK, I have removed my silly comments. For the record, I edited Hasse n-graph, Hasse quiver, Hasse diagram, covering relation, and finite category, not all of them foolishly.
-
- CommentRowNumber11.
- CommentAuthorEric
- CommentTimeOct 24th 2009
Thanks Toby! I really appreciate your help.
The way I think about it is that to form a quiver, you reinterpret each edge of the graph as a morphism and then "fill in all composites". The composites represent paths of length greater than one. Since none of the morphisms in
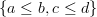 compose, I would think this is a quiver of the Hasse diagram.
compose, I would think this is a quiver of the Hasse diagram.I'm trying to find some arrow theoretic way to talk about the process of constructing an n-poset from some kind of n-diagram. On Hasse diagram, I'm trying to talk about a forgetful functor
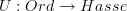
and then look at the free functor
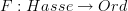
but Hasse hasn't been defined very well yet :)
-
- CommentRowNumber12.
- CommentAuthorTobyBartels
- CommentTimeOct 24th 2009
The poset
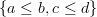 (that's supposed to be a square, with
(that's supposed to be a square, with 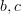 filling both spots at once) does have a composite: the two paths
filling both spots at once) does have a composite: the two paths 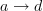 are equal. So the quiver (in the usual sense of free category on a digraph) of the Hasse diagram is different. However, the free poset on the Hasse diagram is correct.
are equal. So the quiver (in the usual sense of free category on a digraph) of the Hasse diagram is different. However, the free poset on the Hasse diagram is correct.So I think that your definition at Hasse diagram is correct: a Hasse diagram is a digraph such that the adjancency relation equals the covering relation, and the poset in question is the free poset (but possibly not the free category) on that digraph.
So now we need to find an analogous condition on
 -digraphs such that each finite
-digraphs such that each finite  -poset is the free
-poset is the free  -poset on an essentially unique such
-poset on an essentially unique such  -digraph, and those should be the Hasse
-digraph, and those should be the Hasse  -diagrams.
-diagrams. -
- CommentRowNumber13.
- CommentAuthorEric
- CommentTimeOct 25th 2009
Phew! I'm glad to hear you say that. Maybe there is hope :)
Yes, that is the idea I'm after. A Hasse n-graph H of an n-poset C is a special (unique?) n-graph such that C is the the free n-poset F(H).
But now I'm confused about whether we want n-graphs or n-computads. I think it comes down to globular sets. Are they necessary or not?
It seems that 2-computads do what I was trying to do for finite categories, but I'm not crazy about requiring the globular identities.
Is there something similar to computad that can generate a bicategory?
-
- CommentRowNumber14.
- CommentAuthorMike Shulman
- CommentTimeOct 25th 2009
What examples do you have that make you not want to require the globular identities?
A 2-computad can actually generate a bicategory just as well as it can a strict 2-category. You take the 1-cells of the bicategory to be arbitrarily associated strings of composites (and units) of the 1-cells in the computad, and then glue in a 2-cell wherever the computad tells you to, together with associativity and unit cells to make it a bicategory. It doesn't matter how you choose to associate the source and target of the 2-cells in the computad; by coherence for bicategories, whatever you choose will give the same bicategory out (up to isomorphism).
It's trickier trying to boost this up a dimension, but the page computad says something about a version for weak n-categories, though I don't know much about that. Presumably one could just imitate the original construction but using a free construction of algebras for some globular operad, rather than free strict n-categories.
-
- CommentRowNumber15.
- CommentAuthorEric
- CommentTimeOct 25th 2009
My aversion to globs is probably not well placed and likely based on poor understanding.
As an example, consider the "walking square" with edges labeled
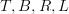 as in the figure on finite category. Then I may be interested in 2-edges
as in the figure on finite category. Then I may be interested in 2-edges 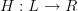 and
and 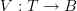 . This is a directed 2-graph that does not satisfy the globular identities.
. This is a directed 2-graph that does not satisfy the globular identities.I admit I don't fully grok computads yet, so I'd be interested in knowing how they would handle this square example.
-
- CommentRowNumber16.
- CommentAuthorEric
- CommentTimeOct 25th 2009
Oh. By the way, just realized I meant double category, not bicategory. Can a computad be used to generate a double category?
-
- CommentRowNumber17.
- CommentAuthorMike Shulman
- CommentTimeOct 25th 2009
- (edited Oct 25th 2009)
An ordinary computad can't generate a double category (at least, not in any particularly useful way), since it only has one kind of 1-cell. But one could easily define a notion of "double computad" that does work for double categories.
Regarding the walking square, why is it that you might be interested in 2-edges H and V? It sounded to me at finite category like you wanted to present the walking square, as a poset, as the 1-truncation of some free 2-category. To do that with a computad, you would have four 0-cells, four 1-cells
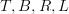 as in the picture, and a 2-cell
as in the picture, and a 2-cell 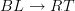 (that is, an element of
(that is, an element of 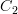 whose source is the free composite
whose source is the free composite 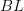 in
in 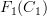 and whose target is the free composite
and whose target is the free composite 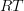 in
in 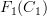 ).
). -
- CommentRowNumber18.
- CommentAuthorEric
- CommentTimeOct 25th 2009
<div> <p>Thanks. I like that explanation of obtaining the walking commutative square from that 2-computad. This is a very meaningful example to me. It is something that Urs and I call a "2-diamond" in our paper.</p> <blockquote>Regarding the walking square, why is it that you might be interested in 2-edges H and V?</blockquote> <p>I have a ton of motivations going on simultaneously. On one hand, I'm trying to understand Tom and Simon's stuff on cardinality of categories and magnitudes of metric spaces. Many of the formulas they write down can be recast into the language of discrete calculus (as developed in Urs' and my paper). However, our work is performed on directed n-graphs containing things like H and V (or so I think). So my intuition is stronger when I'm thinking of directed graphs and directed n-graphs (without the globular identities). I'm hoping that by being able to take a finite category and construct the simplest graph that can reconstruct that category that I can then apply the machinery of discrete calculus on that graph to see if I can reproduce some of their results using things like "discrete curvature". It's a long shot, but my gut tells me it is a worthy pursuit. In the end, I expect some functor to push that machinery through from graphs to categories, but it is not obvious to me how yet, so I'm trying to stick with what is familiar for now.</p> <p>Another motivation is to try to recast the work Urs and I did together into more category friendly language. This is something Urs could probably do in 20 minutes while half asleep, but it has taken me 5 years and I don't think I'm much closer than when I started :)</p> <p>So I'm not sure if I need H and V and I'm definitely not sure I don't, so if possible, I'd like to keep my options open and not restrict things to globs until I convince myself (hopefully with the help from others) that it is the right thing to do.</p> <p>One thing that is curious about our paper is that composition is not degree preserving, i.e. composing and edge with an edge bumps up the dimensionality and gives you a 2-edge. So in our work, <img src="/extensions/vLaTeX/cache/latex_75ba6cbed37dfa47b482d4b39c36f731.png" title="BL" style="vertical-align: -20%;" class="tex" alt="BL"/> and <img src="/extensions/vLaTeX/cache/latex_3f114a65244a8e985a792a6201ff6030.png" title="RT" style="vertical-align: -20%;" class="tex" alt="RT"/> would actually be 2-dimensional oriented cells with <img src="/extensions/vLaTeX/cache/latex_a15156fca2791924d1bb8aa3a8e60b97.png" title="BL = -RT" style="vertical-align: -20%;" class="tex" alt="BL = -RT"/>.</p> </div> -
- CommentRowNumber19.
- CommentAuthorMike Shulman
- CommentTimeOct 26th 2009
I haven't looked at your paper yet, will when I get a moment. What did you think about my comment at finite category that the free functor from n-nonglobular sets (= "directed n-graphs") to n-categories factors through n-globular sets, so that for the purposes of generating free n-categories the extra generality is superfluous?
-
- CommentRowNumber20.
- CommentAuthorEric
- CommentTimeOct 26th 2009
I was very intrigued by that comment and wanted to understand it better. Unfortunately, I'm coming with such a weak background that the statement is not obvious. I still want to understand it. When I have a chance to think about it, I'm sure I'll have some specific questions.
I was afraid that I was polluting finite category, so I started a page Generating Finite Categories, where I hope to explain things in response to your questions at finite category. Still working on it though. Today is a nightmare. Drove 1.5 hrs to my daughters daycare when she informs me she is sick and proceeds to throw up in my car (too much information? :)), drive 1.5 hours home to try to remote into my office and the internet is down. My daughter is fine by the way :) I just got back up and running and should try to get some work done.
1 to 20 of 20
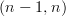 -category, also known as an
-category, also known as an 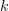 -paths for some
-paths for some 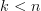 commute, then we might have some kind of
commute, then we might have some kind of 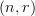 -
-