nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: Question on topologic n-groupoids
Bottom of Page1 to 5 of 5
-
- CommentRowNumber1.
- CommentAuthorMirco Richter
- CommentTimeOct 22nd 2011
- (edited Oct 22nd 2011)
Hi,
this is my first time on nForum and I'll start with a question you people surely can answer:
Suppose we have a topological n-groupoid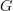 .
.
This can be seen as a Kan simplicial set in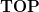 such that all Kan-maps
such that all Kan-maps
are homoeomorphisms for all ).
).
On the other hand we have the simplicial singular complex of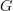 :
:![S G : [n] \mapsto Hom_{Top}(\Delta^n, G) S G : [n] \mapsto Hom_{Top}(\Delta^n, G)](/extensions/vLaTeX/cache/latex_ad4e1105f6c6b596e8e57c00d804f48b.png)
So we have two simplicial sets associated with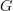 and my question is: Are they related and if yes in what manner?
and my question is: Are they related and if yes in what manner?
-
- CommentRowNumber2.
- CommentAuthorAndrew Stacey
- CommentTimeOct 22nd 2011
(Not an answer: to format mathematics, it is much better to use the Markdown+iTeX filter. The
<latex>...</latex>tags are depreciated. They only work because I’d have to go back and edit a load of old posts if I turned them off. So choose “Markdown+iTeX” from the list at the bottom, and use dollars to surround your maths.) -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeOct 23rd 2011
- (edited Oct 23rd 2011)
Hi Mirco,
when you write “” how are you thinking of as a topological space? Or else, what exactly do you mean to denote?
One way I could make sense of this is that you mean the bisimplicial set which in degree is , where is the topological space of -morphisms in the topological -groupoid (where I am thinking of as a simplicial topological space).
If you mean that, then the answer to the question is: this bisimplicial set is very closely related to itself, in fact it is an equivalent incarnation of it. A detailed discussion of this point is at geometric realization of simplicial topological spaces.
But maybe this is not what you mean. If so, tell us a bit more about what exactly you have in mind.
-
- CommentRowNumber4.
- CommentAuthorMirco Richter
- CommentTimeOct 23rd 2011
- (edited Oct 23rd 2011)
Since is a -groupoid it is a subcomplex of its n-coskeleton and itself a ““-coskeletal simplicial set. If get things right the topological version then just requires that any layer in this set to be a topological space and any map to be continuous. Hence seen all the layers together gives us a single (but N-graded) topological space.
But as I keep the simplicial structure maps, this is what you thought it is.
Anyway thanks for pointing me to the geometric realization of simplicial topological spaces…. Is there something similar for smooth spaces (I guess not, but better asking …)
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeOct 23rd 2011
the topological version then just requires that any layer in this set to be a topological space and any map to be continuous.
So a simplicial topological space is a functor Top from the simplex category. For each it assigns a topological space (I guess this is what you are calling the th “layer”?) and all the face and degeneracy maps between these are continuous maps.
This is, by the way, true whether or not is Kan fibrant in any sense and whether or not it is -coskeletal.
Hence seen all the layers together gives us a single (but N-graded) topological space.
I am still not sure that I see what you mean. That single topological space, is it supposed to be the disjoint uion of the ? If so, that would not be a useful space to look at. But maybe you mean something different?
Is there something similar for smooth spaces (I guess not, but better asking …)
Yes, there is (if I understand correctly what you mean). Most of the things that you would call smooth spaces have an underlying topological space. Therefore many statements generalize directly. We have some discussion to this effect at smooth infinity-groupoid – structures in the section Geometric homotopy. But before getting into that it would be useful to first sort out the topological case.
1 to 5 of 5