nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorDavid_Corfield
- CommentTimeNov 6th 2009
Started MacNeille completion. Is there not a snappy category theoretic way of describing the construction? -
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeNov 6th 2009
The really nice thing would be if it's the poset reflection of the free completion or free cocompletion as a category, although I doubt that it is. But perhaps it is a suitably enriched free (co)completion; I'll think about that.
The characterisation is nice and category-theoretic already; complete lattices form a reflective subcategory of
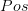 . But presumably you know that, since you linked to completion.
. But presumably you know that, since you linked to completion. -
- CommentRowNumber3.
- CommentAuthorTodd_Trimble
- CommentTimeNov 7th 2009
- (edited Nov 7th 2009)
I think there's a general biclosed bicategory niche into which things like MacNeille completions and Isbell envelopes fit, as follows: if
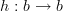 is a 1-morphism in a biclosed bicategory (meaning we have right adjoints to composing with an arrow on either side, i.e., right Kan lifts and right Kan extensions), then for any object $c$ there is a contravariant adjunction between hom-categories
is a 1-morphism in a biclosed bicategory (meaning we have right adjoints to composing with an arrow on either side, i.e., right Kan lifts and right Kan extensions), then for any object $c$ there is a contravariant adjunction between hom-categories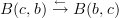
which in one direction maps a 1-morphism
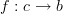 to the Kan lift of
to the Kan lift of 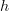 through
through 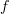 , and in the other maps a 1-morphism
, and in the other maps a 1-morphism 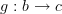 to the right Kan extension of $h$ along
to the right Kan extension of $h$ along 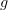 . The point is that we have equivalences
. The point is that we have equivalences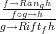
and hence units
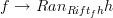 and
and 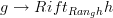 of suitable adjunctions.
of suitable adjunctions.One special case is MacNeille completion, where the bicategory is
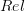 and
and 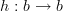 is a binary relation on a set
is a binary relation on a set 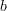 given by a partial order
given by a partial order 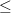 . (The letter 'h'$ is meant to suggest "hom", and at any rate in many practical cases
. (The letter 'h'$ is meant to suggest "hom", and at any rate in many practical cases 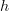 will be a monad in the bicategory, as it is in the case of a partial order seen as a monad in
will be a monad in the bicategory, as it is in the case of a partial order seen as a monad in 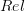 .) A relation
.) A relation 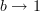 is tantamount to a subset
is tantamount to a subset  of
of 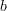 , and the right Kan extension of
, and the right Kan extension of 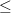 along
along  is
is 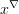 , the set of upper bounds of
, the set of upper bounds of  . Similarly a relation
. Similarly a relation 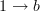 is tantamount to a subset
is tantamount to a subset 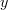 of
of 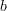 , and the right Kan lift of
, and the right Kan lift of 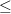 through
through 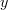 is
is 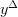 , the set of lower bounds of
, the set of lower bounds of 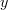 .
.Another example is "conjugation" or "Isbell envelope". Here the bicategory is
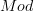 (bimodules between categories), and we can take
(bimodules between categories), and we can take 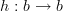 to be any endobimodule, and in particular the unit bimodule
to be any endobimodule, and in particular the unit bimodule 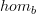 . A 1-morphism
. A 1-morphism 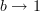 is tantamount to a functor
is tantamount to a functor 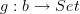 , and the right Kan extension of
, and the right Kan extension of 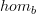 along
along 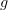 is a 1-morphism
is a 1-morphism 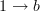 , tantamount to a functor
, tantamount to a functor 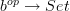 , given by the formula
, given by the formula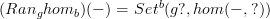
In the other direction, the right Kan lift of
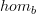 through a 1-morphism
through a 1-morphism 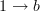 (tantamount to a functor
(tantamount to a functor 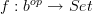 ) is given by the formula
) is given by the formula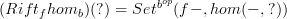
This gives an contravariant adjoint pair
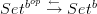 (called conjugation) whose associated monad on
(called conjugation) whose associated monad on 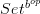 is the Isbell envelope construction.
is the Isbell envelope construction.I think the saturations as in Stacey's work on diffeologies can also be fit in this general framework.
-
- CommentRowNumber4.
- CommentAuthorDavid_Corfield
- CommentTimeNov 7th 2009
That looks very interesting, Todd. Is there a name for this construction to give it a home in nLab? By the way, I'd love to know where material like this comes from. You say "I think" at the beginning of your comment? Are you recalling something you read somewhere, something you heard spoken about, or perhaps something you worked out yourself a while ago? -
- CommentRowNumber5.
- CommentAuthorTodd_Trimble
- CommentTimeNov 7th 2009
- (edited Nov 7th 2009)
The "I think" was unnecessary, I think :-). Maybe I put it there because it the shape of the comment was still being worked out in my head.
When I saw what Toby inserted about Galois connections, I recalled that the typical source of Galois connections between power sets PX and PY is provided by a relation from X to Y. ("I think" I can prove they all arise this way, but I'll get back to that.) So I asked myself: what's the relation in this case? When I saw it was the partial order, which could be interpreted as hom, I recognized it as being a special case of something more general that Lawvere talks about in connection with dualities and adjunctions of algebro-geometric type. The comment then flowed from this observation.
I'll try to think of a good name and home for this in the Lab (there might be one already), but let me see about this typical source here and then I'll check in with Galois connection after I've had some breakfast. Yes, a Galois connection is given by an adjoint pair
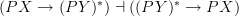 . But the left adjoint part preserves colimits (unions), and since every element in PX is a union of singletons or atoms, it is determined by a functor (function)
. But the left adjoint part preserves colimits (unions), and since every element in PX is a union of singletons or atoms, it is determined by a functor (function) 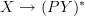 , which is to say a relation from
, which is to say a relation from 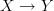 . So the whole adjunction is determined by a relation, and then it's just a matter of calculating the exact formulaic relationship. Something analogous but more general can be made at the level of enriched bimodules.
. So the whole adjunction is determined by a relation, and then it's just a matter of calculating the exact formulaic relationship. Something analogous but more general can be made at the level of enriched bimodules. -
- CommentRowNumber6.
- CommentAuthorTodd_Trimble
- CommentTimeNov 7th 2009
I've just added some remarks to Galois connection on the case of power sets, where they all arise from relations as I indicated above.
-
- CommentRowNumber7.
- CommentAuthorTodd_Trimble
- CommentTimeNov 7th 2009
I've now just consulted the article Isbell envelope, and I got a bit of terminology wrong two comments above, although the general spirit is right. I should not have said that the Isbell envelope is the associated monad on presheaves or co-presheaves; those monads are rather the saturations described in that article. The Isbell envelope is a category, not a monad (knowing full well here that categorical concepts interpenetrate each other to such a degree that e.g. categories are monads if looked at the right way (-: ).
What I really want to think about though is the connection between saturations and bicompleteness. It is the bicompletion aspect that is important to MacNeille completion, and this ought to fit in a more general enriched category theory context, and I dimly recall working through such things a long time ago.
-
- CommentRowNumber8.
- CommentAuthorDavid_Corfield
- CommentTimeNov 10th 2009
Could we start a page for this construction? I guess we'd need a name (Trimble bicompletion?).
And what does "categories are monads if looked at the right way" mean? -
- CommentRowNumber9.
- CommentAuthorTodd_Trimble
- CommentTimeNov 10th 2009
I was planning on doing something like that page, but I was still mulling things over in my slow way. I won't call it Trimble bicompletion though.
Categories as monads: I meant that a category is the same thing as a monad in the bicategory Span; it might be preferable to say "span equipped with a monad structure". -
- CommentRowNumber10.
- CommentAuthorDavid_Corfield
- CommentTimeNov 30th 2009
Added a reference to The Joy of Cats here. It says "A completion of (A,U) that is simultaneously an initial completion and a final completion is called a Mac Neille completion of (A,U)." Are these notions widely accepted? -
- CommentRowNumber11.
- CommentAuthorDavid_Corfield
- CommentTimeDec 3rd 2009
I'm confused as to how 'symmetrical' this construction is in the sense of completion and cocompletion.
According to one description of MacNeille completion it as an injective hull, which is a combination of its being an essential extension and being injective. For posets, an essential extension is such that the embedded poset is join and meet dense. An injective object in poset is complete. So an apparent asymmetry, or does cocompletion come for free?
Todd's description above seems more symmetrical, although he talks of right lifts and right extensions. -
- CommentRowNumber12.
- CommentAuthorTobyBartels
- CommentTimeDec 4th 2009
The Joy of Cats uses a lot of terminology that I haven't seen elsewhere, some of which (like ‘source’) conflicts with terminology that I use a lot.
I like their ideas and wish that I knew more. But in general, I would state it explicitly whenever we draw terminology from them, in case it conflicts with others down the line.
-
- CommentRowNumber13.
- CommentAuthorTobyBartels
- CommentTimeDec 4th 2009
11
So an apparent asymmetry, or does cocompletion come for free?
I'm not sure if this is what you're asking about, but a poset is complete if and only if it is cocomplete.
Arguably, this is not so much about posets as about smallness; a small category is complete if and only if it is cocomplete. Of course, a small category which is either is a p(r)oset! But a large poset can be complete without being cocomplete.
-
- CommentRowNumber14.
- CommentAuthorMike Shulman
- CommentTimeDec 4th 2009
Of course, a small category which is either [complete or cocomplete] is a p(r)oset!
Only if you assume classical logic! The effective topos contains an internal category which is complete and cocomplete in its internal logic, yet not a preorder.
-
- CommentRowNumber15.
- CommentAuthorMike Shulman
- CommentTimeDec 4th 2009
The Joy of Cats uses a lot of terminology that I haven't seen elsewhere, some of which (like ‘source’) conflicts with terminology that I use a lot.
This is getting off-topic, but "source" (and its dual "sink") are not unique to JoC; I think they are fairly common in the literature on topological categories.
-
- CommentRowNumber16.
- CommentAuthorDavid_Corfield
- CommentTimeDec 4th 2009
- (edited Jul 14th 2010)
I’m not sure if this is what you’re asking about, but a poset is complete if and only if it is cocomplete.
Gosh. How have I never realised this? So when it is said that an injective object on Poset is complete, it could have said cocomplete. But is it morally one rather than the other, or both at the same time?
-
- CommentRowNumber17.
- CommentAuthorTobyBartels
- CommentTimeDec 4th 2009
@ Mike
Do you know if we still have a constructive theorem that a small complete category must be cocomplete? That would be neat.
@ David
There is a moral difference, I'm sure. In particular, the equivalence between complete and cocomplete posets does not apply to large posets. It also doesn't apply if you don't accept the existence of (small) power sets, that is if your foundations of mathematics are predicative.
-
- CommentRowNumber18.
- CommentAuthorMike Shulman
- CommentTimeDec 4th 2009
Yes, absolutely. Use the adjoint functor theorem.
-
- CommentRowNumber19.
- CommentAuthorMike Shulman
- CommentTimeDec 4th 2009
A nice example of a large poset which is cocomplete but not complete is the class of pure sets under set-inclusion. Any set of pure sets has a union, so this class is cocomplete, but it has no terminal object.
-
- CommentRowNumber20.
- CommentAuthorTobyBartels
- CommentTimeDec 4th 2009
@ David again
The proof that a complete lattice is injective in the category of posets works just as well for cocomplete lattices. It relies on our asking for injectivity only within the category of small posets but not on the poset itself being small. (That is, even in the category of large posets, a smally complete or smally cocomplete poset is M-injective where M is the class of embeddings of a small poset into a small poset, or into a large one for that matter.) And the argument is predicative; even though there may not be very many complete lattices at all predicatively, the argument applies to any that do exist.
I don't understand the argument in The Joy of Cats for the converse, that an injective poset must be complete, and I haven't come up with my own. But presumably this argument only applies to small posets and is not predicative. (And if it relies on the existence of the MacNeille completion, as JoC suggests, then that is so.)
-
- CommentRowNumber21.
- CommentAuthorTobyBartels
- CommentTimeDec 5th 2009
@ Mike
A simpler (from a structural perpsective) example is the class of well-ordered sets, or equivalently the class of ordinal numbers. It works the same way: suprema and inhabited infima, but no top.
-
- CommentRowNumber22.
- CommentAuthorMike Shulman
- CommentTimeMay 7th 2018
1 to 22 of 22