nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
Fixed the comments in the reference list at model structure on dg-algebras: Gelfand-Manin just discuss the commutative case. The noncommutative case seems to be due to the Jardine reference. Or does anyone know an earlier one?
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
I have a question at model structure on dg-algebras on the invariant characterization of commutative dg-algebras within all dg-algebras.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
I added an "Idea" section to model structure on dg-algebras
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
- (edited Nov 11th 2009)
I added a theorem from the book by Igor Kriz and Peter May about how commutative dg-algebras already exhaust, up to weak equivalence, all homotopy-cmmutative dg-algebras to model structure on dg-algebras.
(this might better fit into some other entry eventually, though)
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeNov 11th 2009
Added the statement that the forgetful functor from commutative dg-algebras to all dg-algebras is the right adjoint part of a Quillen adjunction with respect to the given modelstructures.
-
- CommentRowNumber6.
- CommentAuthorzskoda
- CommentTimeNov 11th 2009
I would look into Hinich's 1995 or so paper, for a possible earlier reference. -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeNov 12th 2009
- (edited Nov 12th 2009)
created a section on cofibrations in CdgAlg and hence on Sullivan algebras.
Created entry for Dennis Sullivan in that context. Always nice to create an entry and see that the "timeline"-entry was already requesting it.
I suppose I'll have the following sorted out in a minute, but maybe somebody is quicker with helping me:
in the definition of a relative Suillvan algebra
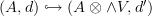 I suppose we do require that
I suppose we do require that 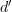 restricted to
restricted to 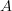 acts like
acts like 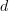 plus a term that contains elements in V ?
plus a term that contains elements in V ? -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeNov 29th 2010
I started at model structure on dg-algebras a new subsection on Unbounded dg-algebras, stating a basic existence result.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeDec 9th 2010
added a section Simplicial hom-objects to model structure on dg-algebras on the derived hom-spaces for unbounded commutative dg-algebras (over a field of char 0).
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeDec 9th 2010
- (edited Dec 9th 2010)
okay, I think I finally have assembled the full proof that the derived copowering of undbounded commutative dg-algebras (over field of char 0) over degreewise finite simplicial sets is given by the polynomial-differential-forms-on-simplices-functors. I have written this out now at Derived powering over sSet.
This provides the missing detail for the discussion that over at Hochschild cohomology. This is supposed to be all very obvious, but it took me a bit to assemble all the details properly, anyway.
I now moved other discussion of the model structure on commutative unbounded dg-algebras from the Hochschild entry over to model structure on dg-algebras. This mainly constituting the other new section Derived co-powering over sSet.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeDec 10th 2010
I added statement and proof that is a Kan complex when is cofibrant.
Also added an earlier reference by Ginot et al where it is discussed that their “derived copowering” of cdgAlg over sSet indeed lands in commutative dg-algebras. I’ll try to add more technical details on how this works later on.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeJul 16th 2014
- (edited Jul 16th 2014)
there was an old question of how (to which extent) the homotopy theory of commutative dg-algebras is homotopy-faithful inside that of all dg-algebras.
Recently there appeared some discussion of this issue in
Ilias Amrani, Comparing commutative and associative unbounded differential graded algebras over Q from homotopical point of view (arXiv:1401.7285)
Ilias Amrani, Rational homotopy theory of function spaces and Hochschild cohomology (arXiv:1406.6269)
I have added pointers to this here.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeFeb 21st 2017
- (edited Feb 21st 2017)
I have added to the section on the Bousfield-Gugenheim model structure a subsection on its simplicial hom-complexes which almost but not quite, make for a simplicial model category structure.
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeAug 19th 2020
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeAug 19th 2020
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeAug 21st 2020
- (edited Aug 21st 2020)
Added full publication data to:
- Paul Goerss, Kirsten Schemmerhorn, Model categories and simplicial methods, Notes from lectures given at the University of Chicago, August 2004, in: Interactions between Homotopy Theory and Algebra, Contemporary Mathematics 436, AMS 2007(arXiv:math.AT/0609537, doi:10.1090/conm/436)
Around Example 3.7, these authors make (somewhat implicitly) the observation that the Bousfield-Gugenheim model structure on connective rational dgc-algebras (which B&G and later Gelfand&Manin establish by laborious checks) is simply that right transferred from the projective model structure on chain complexes – which makes the proof that relative Sullivan models are cofibrations a triviality.
So this is all very nice, and highlighted as such in Hess’s recview. But neither of these authors states this as a theorem that could be properly cited as such, instead they leave it at side remarks. Is there any author who has published this in more citeable form?
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeAug 23rd 2020
added paragraph on the Quillen adjunction between simplicial sets and connective dgc-algebras
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeSep 1st 2020
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeJul 7th 2021
-
- CommentRowNumber20.
- CommentAuthorTodd_Trimble
- CommentTimeJul 11th 2021
Changed to .
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeJul 11th 2021
Ah, right. Thanks.
1 to 21 of 21