nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorTobyBartels
- CommentTimeNov 12th 2009
I've been thinking about a pedagogical problem, so now I've written something about it at category theory vs order theory. Comments and examples welcome!
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeNov 12th 2009
I like this a lot.
I would, for instance, love to be educated more about the approach where we don't study topological spaces at all, but just locales.
Or rather, my impression is this:
if we use topological spaces not up to homotopy, then we really mean locales.
if we use topological spaces in homotopy theory, then we really mean oo-groupoids.
-
- CommentRowNumber3.
- CommentAuthorTobyBartels
- CommentTimeNov 12th 2009
I have a third item: convergence spaces. Sometimes we seem to care about whether some things converge to another, in a topological sense, yet the convergence is not topological (or if topological, at least not sobre) so that locales don't apply. (And homotopy theory is definitely not the issue.) But I don't understand this well enough yet; perhaps locales can do that somehow. (Standard example of a highly nontopological convergence: convergence in measure.)
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeNov 12th 2009
I felt like it and started order theory. Not meaning to steal this topic from you. Just thought it would be nice to have a stub for this entry being existent to go along with the versus-version.
I also edited poset a little, added a toc and editing the subsection on "In higher category theory".
I am thinking we should link to order theory somehow from the higher category theory page or its table of contents. But not sure yet how to phrase that best.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeNov 12th 2009
- (edited Nov 12th 2009)
There is a book which does standard point-set topology entirely in terms of locales. That's Johnstone's "Stone Spaces", right? (I looked at it once after Todd pointed me to it, but don't remember the book as a whole).
If so, it would be nice if at the reference section at locale somebody would add a comment on this book there, saying a bit about what it accomplishes.
-
- CommentRowNumber6.
- CommentAuthorTobyBartels
- CommentTimeNov 13th 2009
Yeah, I started going through it: Stone Spaces. But then I didn't get very far last time, maybe I should try again.
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeNov 13th 2009
Ah, right.
I added to the reference at locale now a sentence alerting the reader explicitly about this.
-
- CommentRowNumber8.
- CommentAuthorTobyBartels
- CommentTimeNov 13th 2009
I made order theory refer to
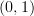 -categories rather than
-categories rather than 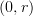 -categories. Of course, every
-categories. Of course, every 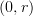 -category (for
-category (for 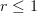 , and I don't know what else it could mean for
, and I don't know what else it could mean for 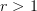 ) is a
) is a 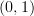 -category, but the point is that
-category, but the point is that  might be larger than
might be larger than  , rather than smaller (as is usually the point when
, rather than smaller (as is usually the point when  is brought up).
is brought up). -
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeNov 13th 2009
Okay, good.
I like the idea of a very low-dimensional higher category theorist.
You should establish that term: very low dimensional theory .
-
- CommentRowNumber10.
- CommentAuthorMike Shulman
- CommentTimeNov 13th 2009
I have believed for some time that the right way to teach the adjoint functor theorem is to do the poset version first. It has all the intuition but none of the fiddly size issues. Same with the initial algebra theorem (whose poset version is sort of the Knaster-Tarski theorem).
On the other hand, order theory doesn't tell you much about the monadicity theorem, since all monads on posets are idempotent.
-
- CommentRowNumber11.
- CommentAuthorMike Shulman
- CommentTimeNov 13th 2009
I also agree that locales should be learned before Grothendieck topoi. There's also a case to be made, however, that ionads should also be learned before Grothendieck topoi, since Grothendieck topoi can be regarded as the minimal common generalization of locales and ionads.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeNov 13th 2009
-
- CommentRowNumber13.
- CommentAuthorDavid_Corfield
- CommentTimeNov 13th 2009
This is all very interesting. In view of Mike's mention of a 'minimal common generalization' to suggest both things to be generalized should be learned first, can we take it that not only should posets be learned before categories, but also monoids. -
- CommentRowNumber14.
- CommentAuthorTobyBartels
- CommentTimeNov 13th 2009
I think that people usually learn all of the group theory that is relevant before learning category theory. Sometimes it may be useful to see something for monoids or groupoids before categories, when it is trivial for groups; for example, groupoids have natural (or canonical) transformations, and monoids have nontrivial idempotents. On the other hand, category theory students often do learn a lot about groupoids, since they primarily see these (unlike the others) as special categories; I think that order theory is unduly neglected.
In any case, it's been unduly neglected in my education, and I'm trying to fix that!
categories / | \ orders groupoids monoids \ / \ / sets groups \ / trivialSomebody should put this diagram on the lab somewhere …
-
- CommentRowNumber15.
- CommentAuthorTobyBartels
- CommentTimeNov 13th 2009
- (edited Nov 13th 2009)
Re: ionads
I shall have to read Garner's paper, of course. But my feeling these days is that one should not bother with Bourbaki's topological spaces at all, but go straight from metric spaces (or whatever one considers to be sufficient motivation) to locales (or to simplicial sets, or to convergence spaces, depending on what one is after).
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeNov 13th 2009
<div> <blockquote> But my feeling these days is that one should not bother with Bourbaki's topological spaces at all, </blockquote> <p>That resonates well with my impression.</p> <p>It's still good to have an entry on those ionads. Maybe we can accompany the link to <a href="https://ncatlab.org/nlab/show/ionad">ionad</a>s from <a href="https://ncatlab.org/nlab/show/locale">locale</a> with a bit more commentary.</p> </div> -
- CommentRowNumber17.
- CommentAuthorMike Shulman
- CommentTimeNov 13th 2009
There isn't really anything that I would consider "sufficient motivation" for locales short of topological spaces. Not that one couldn't in theory teach locales without teaching topological spaces, but I think it would be gratuitously difficult. The notion of "open set" is so natural and ubiquitous in mathematics. And a lot of locale theory is much more complicated and categorically sophisticated than the corresponding parts of ordinary topological-space theory. Just compare the definitions of a "subspace" and of a "sublocale"! Locales may be "morally the right notion" in many cases (I am not convinced of all cases), but I wouldn't have wanted to have to learn them as an undergraduate.
And since topological spaces suffice not just for undergraduates, but many other places in mathematics that topology is used (from various kinds of geometry all the way to descriptive set theory), it seems silly to me to want to get rid of them. Locales are not much good, as far as I can tell, as models for
 -groupoids. Simplicial sets are great for some things, but fare badly for other things (e.g. sometimes it's very nice to have a model category where everything is fibrant). Also some things you want to consider as
-groupoids. Simplicial sets are great for some things, but fare badly for other things (e.g. sometimes it's very nice to have a model category where everything is fibrant). Also some things you want to consider as  -groupoids, like manifolds, come to you naturally as spaces. And while various kinds of convergence spaces have advantages and should be better known, they also have their disadvantages, and I don't see any reason to give them a blanket preference over topological spaces.
-groupoids, like manifolds, come to you naturally as spaces. And while various kinds of convergence spaces have advantages and should be better known, they also have their disadvantages, and I don't see any reason to give them a blanket preference over topological spaces. -
- CommentRowNumber18.
- CommentAuthorTobyBartels
- CommentTimeNov 14th 2009
I mention convergence spaces only because sometimes one seems to want that level of generality, and I only know how to do it with structured sets of points. But there's no need to bring them up to undergraduates if topological spaces —or locales or simplicial sets— will do.
It's true that neither locales nor simplicial sets suffice for all of the purposes that topological spaces meet. However, it is easy enough to construct a simplicial set from a locale, so that takes care of the situation where we want to do homotopy theory of manifolds. In going the other way, it's important that any simplicial set is weakly equivalent to a CW complex, which is a metric space; do we ever need to mention the definition of topological spaces to discuss this?
And it is not true that a manifold comes to us as a topological space! It comes to us a set equipped with an atlas of charts, and the topology is defined in terms of that; it is just as easy to define a locale in terms of that data. It is true that a lot of books will define a manifold as a topological space equipped with an atlas of charts, but this is completely unnecessary; at best, it gives them an easy place to stick in requirements that the manifold be Hausdorff and paracompact (which could be done at the localic level, although I would rather simply require metrisability if you need this at all).
So what's left is whether locale theory is as simple to present as the theory of topological spaces. Maybe you are right that it is not, but I'm not convinced. (Maybe subspaces are more complicated, but quotient spaces are easier!) I'd like to try to write an introductory upper-undergraduate level textbook on topology that takes locales as the basic notion. (The corresponding task for homotopy theory using simplicial sets has already been done.) Maybe nobody has done this because it doesn't really work, but so far my intuition is that it would work.
I need to learn more locale theory to know for certain, however.
-
- CommentRowNumber19.
- CommentAuthorTobyBartels
- CommentTimeNov 14th 2009
I should say something more about motivation. Of course open sets are ubiquitous in mathematics, but this motivates the definition of a locale as easily as a topological space. Every metric space (the usual motivation in an introductory course) has a frame of open sets, and we see that we can describe any continous function between metric spaces in terms of the corresponding frames —that is the motivation. Normally one takes it as motivating the definition of a topological space as a set equipped with a subframe of its power set (with a continuous map as a function that induces a frame homomorphism the other way), but I would take it as motivating the definition of a locale as a frame (with a continuous map as a frame homomorphism).
-
- CommentRowNumber20.
- CommentAuthorMike Shulman
- CommentTimeNov 14th 2009
it's important that any simplicial set is weakly equivalent to a CW complex, which is a metric space
Not every CW complex is a metric space. Metric spaces are, among other things, first countable, which CW complexes are in general not.
Maybe subspaces are more complicated, but quotient spaces are easier!
Perhaps it's slightly easier to define a subframe than a quotient space. But I think whatever gain there is there is immediately lost by the attendant difficulty of reversing all the arrows and figuring out in exactly what way a subframe should be thought of as a quotient "space." The intution of quotient spaces that one is "identifying" or "gluing" certain points together is lost if you don't have points.
The corresponding task for homotopy theory using simplicial sets has already been done.
What textbook are you referring to? I'm not aware of any such book that I would recommend to someone learning homotopy theory for the first time.
Of course open sets are ubiquitous in mathematics, but this motivates the definition of a locale as easily as a topological space.
What motivates you to throw away the points? Especially since by doing so you make so many things harder?
-
- CommentRowNumber21.
- CommentAuthorTobyBartels
- CommentTimeNov 14th 2009
Not every CW complex is a metric space.
Oh, huh. I guess that every CW complex is a colimit of metric spaces, but this colimit is not necessarily metrisable. I still think that this ought to be describable in a fairly straightforward way in localic terms, if you need it (since every CW complex is Hausdorff, hence sobre).
Perhaps it's slightly easier to define a subframe than a quotient space.
You say ‘perhaps slightly easier’ here but ‘much more complicated’ elsewhere; I don't think that you're being fair!
The intution of quotient spaces that one is "identifying" or "gluing" certain points together is lost if you don't have points.
Why is that your intuition of forming a quotient space? For what it's worth, my intuition is that we are identifying or gluing together regions of arbitrary shape, not necessarily points. It is the influence of point-set topology that makes us see things as fundamentally about points; open-set topology will be different.
What textbook are you referring to?
John Baez showed it to me, but I'll have to look up what it was again.
What motivates you to throw away the points?
Mostly hopes of getting a simple theory that is also constructively valid. So not anything likely to appeal to teachers of undergraduate topology, I'm afraid.
-
- CommentRowNumber22.
- CommentAuthorMike Shulman
- CommentTimeNov 14th 2009
- (edited Nov 14th 2009)
BTW, Hausdorff spaces are only necessarily sober under classical logic. (-: If you assume classical logic, so that your CW complexes are sober, then of course you could do all of CW-complex theory in the category of spatial locales, since that's equivalent to the category of sober spaces. But why would you want to?
Also worth noting are
- the lack of "small objects" in the category of locales, so that the usual model-categorical sort of arguments don't work,
- the lack (according to current knowledge) of a good theory of "compactly generated" locales which might be cartesian closed
- the fact that cartesian products of spatial locales in Loc are not, in general, spatial. In particular,
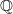 is not a localic group, because the locale product
is not a localic group, because the locale product 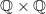 is "bigger" than the topological-space product and the addition map can't be extended to it. That means that if you want to "work in the category of spatial locales" you end up applying the "spatialization" functor a lot---so what have you really gained over just working with spaces?
is "bigger" than the topological-space product and the addition map can't be extended to it. That means that if you want to "work in the category of spatial locales" you end up applying the "spatialization" functor a lot---so what have you really gained over just working with spaces?
You say ‘perhaps slightly easier’ here but ‘much more complicated’ elsewhere; I don't think that you're being fair!
It is my opinion that a lot of locale theory is much more complicated than the corresponding parts of point-set topology. The particular aspect of quotient objects is not part of that "lot", and for that case it is my opinion that the locale version is perhaps slightly easier. You obviously disagree, but I don't see any question of fairness; I'm just stating what seems to me to be the case. A function f can be much greater than another function g on most of its domain, but only slightly less than it on other parts of its domain; nothing unfair about that.
Mostly hopes of getting a simple theory that is also constructively valid. So not anything likely to appeal to teachers of undergraduate topology, I'm afraid.
Exactly my point. Or part of it, anyway.
-
- CommentRowNumber23.
- CommentAuthorMike Shulman
- CommentTimeNov 14th 2009
By the way, I'm not sure whether "sobre" was intentional, but even Brits spell that word with an "er". (-:
-
- CommentRowNumber24.
- CommentAuthorTobyBartels
- CommentTimeNov 14th 2009
No, I don't want to work with spatial locales, just with locales. If things don't work there, then my programme fails.
As for the spelling, I must have been writing in French.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeNov 16th 2009
<div> <blockquote> Locales are not much good, as far as I can tell, as models for <img src="/extensions/vLaTeX/cache/latex_ff52bcaf24f3d4af5a2a50cf5200b74f.png" title="\infty" style="vertical-align: -20%;" class="tex" alt="\infty"/>-groupoids. </blockquote> <p>Yes. Further above we said (or I did, butt I think Toby agreed) that</p> <p>topological spaces appear either in a context where homotopies are taken into account, then they are "really" <img src="/extensions/vLaTeX/cache/latex_e8506f04cc9a9e5fc8348eb71b07e2ce.png" title=" \infty " style="vertical-align: -20%;" class="tex" alt=" \infty "/>-groupoids</p> <p>or in a context where homotopy is not taken into account, then they are "really" locales.</p> <p>Of course this doesn't imply that one should stop talking about or teaching topological spaces. But it does seem to be helpful conceptually to keep this "deeper reality" in mind.</p> </div> -
- CommentRowNumber26.
- CommentAuthorMike Shulman
- CommentTimeNov 16th 2009
Saying that the notion of topological space is not a fundamental one, but is a convienient device used in practice either as a way to model either
 -groupoids or locales, is one thing. I'm not sure I agree with it, but I can at least see where it's coming from. (I would want to make a much more comprehensive study of the uses of topology everywhere in mathematics before agreeing with it. Is it never, ever important anywhere in mathematics that
-groupoids or locales, is one thing. I'm not sure I agree with it, but I can at least see where it's coming from. (I would want to make a much more comprehensive study of the uses of topology everywhere in mathematics before agreeing with it. Is it never, ever important anywhere in mathematics that 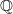 is a topological group (and not just an infinite loop space)? I am skeptical.) But I think Toby was saying something stronger, that topological spaces should not even be taught, and that I definitely disagree with.
is a topological group (and not just an infinite loop space)? I am skeptical.) But I think Toby was saying something stronger, that topological spaces should not even be taught, and that I definitely disagree with. -
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeNov 16th 2009
- (edited Nov 16th 2009)
<div> <blockquote> Is it never, ever important anywhere in mathematics that <img src="/extensions/vLaTeX/cache/latex_dd6b364a24ced34fddb1304405e2b85b.png" title=" \mathbb{Q} " style="vertical-align: -20%;" class="tex" alt=" \mathbb{Q} "/> is a topological group (and not just an infinite loop space)? </blockquote> <p>It is certainly important when talking about <em>models</em> for the oo-loop space <img src="/extensions/vLaTeX/cache/latex_dd6b364a24ced34fddb1304405e2b85b.png" title=" \mathbb{Q} " style="vertical-align: -20%;" class="tex" alt=" \mathbb{Q} "/>. One could say that you have a model for the oo-groupoid which comes naturally equipped with the extra structure of a group-locale.</p> <p>I am thinking that from a fundamental perspective (not necessarily for teaching this) this may be helpful, as it shows clearly that these are two different conceptual aspects of the object <img src="/extensions/vLaTeX/cache/latex_dd6b364a24ced34fddb1304405e2b85b.png" title=" \mathbb{Q} " style="vertical-align: -20%;" class="tex" alt=" \mathbb{Q} "/>. It is a bit like using types: by using the locale-perspective we do remember that the notion of topological space is used <em>not</em> up to homotopy when we say "topological group".</p> <p>Elsewhere in discussions of oo-groupoids and (oo,1)-categories one sees warnings along the lines: "Topologists should beware that we are interested in topological spaces only up to homotopy. For instance all topological vector spaces are trivial for us, as they all represent the point."</p> <p>If one were not mixing the two uses of topological spaces, such warning were not necessary and we could make nice statements like: a topological vector space may be very interesting as a locale, but is very boring as an oo-groupoid.</p> </div> -
- CommentRowNumber28.
- CommentAuthorMike Shulman
- CommentTimeNov 16th 2009
One could say that you have a model for the oo-groupoid which comes naturally equipped with the extra structure of a group-locale.
That's the whole point:
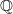 is not a localic group. It is of course a topological group, but the locale product
is not a localic group. It is of course a topological group, but the locale product 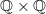 is "bigger" than the product as topological spaces, and the group structure map
is "bigger" than the product as topological spaces, and the group structure map 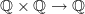 doesn't extend to the locale product.
doesn't extend to the locale product. -
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeNov 16th 2009
Ah, I wasn't aware of that.
-
- CommentRowNumber30.
- CommentAuthorTobyBartels
- CommentTimeNov 17th 2009
But I think Toby was saying something stronger, that topological spaces should not even be taught, and that I definitely disagree with.
I wouldn't go so far as to say that, although it might be true.
I wouldn't go so far as to say that. But I rather suspect that locales should be taught, and perhaps should be taught to undergraduates before topological spaces. I should first figure out enough of how to do that to convince you that it works, however.
-
- CommentRowNumber31.
- CommentAuthorMike Shulman
- CommentTimeNov 17th 2009
I agree that locales should be taught. Possibly even to undergraduates. (I've taught them to high school students!) I don't think, at the moment, that they should be taught before topological spaces, but I can maybe see an argument for teaching the two concurrently, as in Vickers' book "Topology via Logic".
My feeling that you were saying topological spaces should not even be taught came from this quote:
But my feeling these days is that one should not bother with Bourbaki's topological spaces at all, but go straight from metric spaces (or whatever one considers to be sufficient motivation) to locales
-
- CommentRowNumber32.
- CommentAuthorzskoda
- CommentTimeNov 17th 2009
In noncommutative algebraic geometry open subsets are replaced by flat localizations. The descent for quasicoherent sheaves exhibits the phenomenon that the comparison between different localizations should be done both at $Q_1 Q_2 A$ and $Q_2 Q_1 A$. This is like having two different intersections of open sets which are not-isomorphic. Plus the cover when "intersected" with another localization is not a cover of that localization (like having non-distributive lattice). So even sheaf theory is quite different. Despite all of these in a number of situations, the usage of localizations is essential, and parallel to the one in commutative algebraic geometry. -
- CommentRowNumber33.
- CommentAuthorTobyBartels
- CommentTimeNov 18th 2009
For the record, I just stumbled across again what probably sent me off into the wilderness of thinking that locales are more important than Bourbaki spaces (as Paul Taylor calls them): this essay by Johnstone.
-
- CommentRowNumber34.
- CommentAuthorMike Shulman
- CommentTimeNov 18th 2009
Yes, that's a very nice essay. I agree wholeheartedly that locales are better than spaces in many ways, and have the potential to make a much bigger difference in mathematics. I would especially like to see wider application of the equivalence
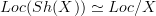 . All I'm saying is that I'm not yet convinced that the notion of topological space can be discarded entirely, for both mathematical and pedagogical reasons.
. All I'm saying is that I'm not yet convinced that the notion of topological space can be discarded entirely, for both mathematical and pedagogical reasons. -
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeNov 18th 2009
- (edited Nov 18th 2009)
Thanks for the link to Johnstone's essay. I added it to the reference list at locale.
So, just for the record, on page 4 of this essay is the example of the topological space
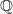 that Mike mentioned above.
that Mike mentioned above.Johnstone says, following Isbell, that
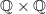 is the "wrong thing to consider", while the localic product
is the "wrong thing to consider", while the localic product 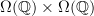 is the right one, from some point of view.
is the right one, from some point of view.So I find it curious that
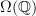 fails to be a group locale. Is it maybe at least a group locale up to something?
fails to be a group locale. Is it maybe at least a group locale up to something? -
- CommentRowNumber36.
- CommentAuthorDavid_Corfield
- CommentTimeNov 18th 2009
-
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeNov 18th 2009
Okay, thanks. I have added that link to the entry. Hope you don't mind.
-
- CommentRowNumber38.
- CommentAuthorTobyBartels
- CommentTimeNov 18th 2009
- (edited Nov 18th 2009)
Yeah, David's link is better, it's just not the one that I in fact stumbled across.
As for the localic group
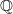 , it's interesting. One thing that I can say is this: if you're interested in rational numbers for themselves, then you might as well just use the discrete topology; then it's a localic group, no problem. If you put the absolute-value metric on it, however, then presumably you want to complete that and so deal with the real line, and this is a localic group (although constructively, at least, it may not be spatial); hopefully the various prime-adic topologies work the same way. But it is still a little disconcerting that the subspace
, it's interesting. One thing that I can say is this: if you're interested in rational numbers for themselves, then you might as well just use the discrete topology; then it's a localic group, no problem. If you put the absolute-value metric on it, however, then presumably you want to complete that and so deal with the real line, and this is a localic group (although constructively, at least, it may not be spatial); hopefully the various prime-adic topologies work the same way. But it is still a little disconcerting that the subspace 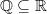 is not a subgroup. Somehow it fails to be closed under addition, even though it is pointwise closed; very odd.
is not a subgroup. Somehow it fails to be closed under addition, even though it is pointwise closed; very odd.Mike, do you have a reference for the failure of
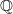 to be a localic group, so that I can look at it in more detail?
to be a localic group, so that I can look at it in more detail? -
- CommentRowNumber39.
- CommentAuthorDavid_Corfield
- CommentTimeNov 18th 2009
No, I should have done it myself. I always wonder about linking to large files. Does anyone still have a problem downloading 1.5MB, or are people who use nLab always on a reasonable fast broadband connection? -
- CommentRowNumber40.
- CommentAuthorUrs
- CommentTimeNov 18th 2009
- (edited Nov 18th 2009)
I am usually on fast broadband, except when on the train or on weekends. But usually I download documents while on broadband and store them, to read them later.
-
- CommentRowNumber41.
- CommentAuthorUrs
- CommentTimeNov 18th 2009
- (edited Nov 18th 2009)
-
-
- CommentRowNumber42.
- CommentAuthorTobyBartels
- CommentTimeNov 18th 2009
I didn't notice that the file was large at all; that shows you what my connection's like. (^_^)
-
- CommentRowNumber43.
- CommentAuthorMike Shulman
- CommentTimeNov 18th 2009
In chapter II 2.14 of Stone Spaces, Johnstone describes explicitly a relation between certain unions of open rectangles that holds in
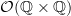 but fails in
but fails in 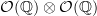 . He refers to this in "The point of pointless topology" when he says
. He refers to this in "The point of pointless topology" when he saysWhilst it is possible (see [35, II 2.14]) to give an explicit description of (at least some of) the extra relations which hold in
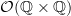 , all such relations seem to be inordinately complicated, and they appear accidental coincidences rather than expressions of any intuitive idea of how open rectangles ought to behave. That is, we should think of
, all such relations seem to be inordinately complicated, and they appear accidental coincidences rather than expressions of any intuitive idea of how open rectangles ought to behave. That is, we should think of 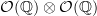 as expressing what
as expressing what 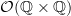 really ought to be, were it not for the unfortunate fact that we are obliged (if we stay within the category of spaces) to represent it as a lattice of subsets of
really ought to be, were it not for the unfortunate fact that we are obliged (if we stay within the category of spaces) to represent it as a lattice of subsets of 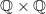 .
.There's something to be said for that point of view. On the other hand, I think the discrepancy (and the inordinate complication of the additional relations) can just as easily be read as indicating that the "algebraic" notion of frame is incapable of capturing the real "spatial/topological" behavior of topological spaces.
The failure of the
 to be a localic group also follows from the fact that any subgroup of a localic group is closed, while
to be a localic group also follows from the fact that any subgroup of a localic group is closed, while  is of course not closed in
is of course not closed in 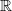 . A proof of this can be found in the Elephant.
. A proof of this can be found in the Elephant. -
- CommentRowNumber44.
- CommentAuthorUrs
- CommentTimeNov 18th 2009
- (edited Nov 18th 2009)
Maybe we can refine our hunch that ""topological spaces that are not regarded up to homotopy" should be something categori(c)al:
as we said elsewhere, the idea is that we just use (oo,1)-toposes as formal duals to "spaces not up to homotopy"
and regard topological spaces as 0-localic (oo,1)-toposes. And there is a difference between n-localic (oo,1)-toposes and plain (n,1)-toposes. In our case: a locale, being a 0-topos, is almost but not quite the same as a 0-localic (oo,1)-topos. I am guessing that this is what we are seeing here. (?)
-
- CommentRowNumber45.
- CommentAuthorMike Shulman
- CommentTimeNov 18th 2009
I'm not sure what you're getting at. The (2-)category of locales is equivalent to the 2-category of localic 1-topoi, in a way that preserves products and hence all of the pathology of
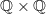 . I'm not as familiar with
. I'm not as familiar with 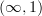 -topoi, but I would expect the same to be true there.
-topoi, but I would expect the same to be true there. -
- CommentRowNumber46.
- CommentAuthorUrs
- CommentTimeNov 18th 2009
Oh, is it? I thought it was different. Okay, then that was a wrong idea!
-
- CommentRowNumber47.
- CommentAuthorUrs
- CommentTimeNov 18th 2009
- (edited Nov 18th 2009)
Mike,
I added this statement here.
Let me know if it's right this way.
I eventually also would like a discussion of the 2-category of all toposes, then.
-
- CommentRowNumber48.
- CommentAuthorTobyBartels
- CommentTimeNov 19th 2009
- (edited Nov 19th 2009)
@ Mike
The failure of the
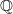 to be a localic group also follows from the fact that any subgroup of a localic group is closed, while
to be a localic group also follows from the fact that any subgroup of a localic group is closed, while 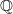 is of course not closed in
is of course not closed in 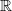 . A proof of this can be found in the Elephant.
. A proof of this can be found in the Elephant.The index of the Elephant is not helping me to find a proof that any subgroup of a localic group is closed. (’_‘)
-
- CommentRowNumber49.
- CommentAuthorzskoda
- CommentTimeNov 19th 2009
In noncommutative algebraic geometry we deal with lattices of good localizations, for example of hereditary torsion theories in module categories. The lattice in question is not used for gluing, rather the single meet on the lattice is replaced by the two consecutive localizations (for covers of two elements). Moreover, the lattice is NOT distributive. If one makes a meet of a cover with another localization, one does not get a cover of the obtained localization (this is not that crucial for descent as one can use also localizations in other order and together they suffice for gluing). Intuition on these localizations is similar to the intuition about locales (at least at the basic level in which I know few things about locales). I wish locale experts from nlab would get interested in lattices of localizations as sort of nc spaces... -
- CommentRowNumber50.
- CommentAuthorMike Shulman
- CommentTimeNov 19th 2009
@Toby: C5.3
-
- CommentRowNumber51.
- CommentAuthorMike Shulman
- CommentTimeNov 19th 2009
BTW, for anyone who doesn't feel like tracing through the proof in the Elephant to see why any subgroup of a localic group is closed, the basic fact it uses (which is false for topological spaces) is that the intersection of any two dense sublocales is again dense. I summarized the proof at localic group.
-
- CommentRowNumber52.
- CommentAuthorUrs
- CommentTimeNov 19th 2009
Thanks. I added a toc and hyperlinks at localic group.
-
- CommentRowNumber53.
- CommentAuthorTobyBartels
- CommentTimeNov 20th 2009
@ Mike
Thanks!
-
- CommentRowNumber54.
- CommentAuthorGuest
- CommentTimeMay 1st 2022
1 to 54 of 54