Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Discussion Tag Cloud

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: Theta category

Bottom of Page

1 to 7 of 7

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeNov 17th 2009
    • (edited Nov 13th 2012)

    created Theta category (made disk category a redirect).

    In the "Idea" section I had the idea that the quickest way to define 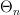\Theta_n is as the full subcategory of strict n-catgeories on n-computads. Is that right? If not, something along these lines must be right.

    • CommentRowNumber2.
    • CommentAuthorMike Shulman
    • CommentTimeNov 17th 2009

    No, not computads, there would be far too many of those. Computads contain cells whose source and target are arbitrary composites, rather than single cells. It should be the full subcategory of strict n-categories on some objects, which are free in some sense -- free on a finite tree, probably. Have you looked at the paper "the universal property of the multitude of trees"?

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeNov 18th 2009

    I fixed the sentence about computads and mention the definition of 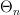\Theta_n as the category of planar rooted trees of level 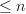\leq n . Added some pictures.

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeMay 18th 2012
    • (edited May 18th 2012)

    I have expanded Theta category: added the definition in terms of categorical wreath product and added various properties resulting from that and references related to that.

    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeNov 13th 2012

    add brief remark that Theta is the formal dual of the finite disk category in analogy to how $\Delta$ is the opposite of the category of finite strict linear intervals. But no details yet. More a reminder for things to be expanded on.

    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeNov 13th 2012

    Added a link to a scan of Joyal’s original preprint on Θ!A = \sum_{E: V} (E \to A}\Theta-categories.

  7. Fixed broken links

    Matt Feller

    diff, v31, current

1 to 7 of 7

  1.