nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeNov 18th 2009
commented in the discussion at point of a topos and have a question there.
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeNov 18th 2009
- (edited Nov 18th 2009)
As I mention gluing categories from localizations, I created the corresponding entry in my personal lab area. All comments are welcome (I created it quickly from my old notes and papers, so it needs polishing anyway). Wrote a small entry additive monad in common nlab. My interest is in replacing gluing of categories with gluing corresponding representable functors, but the setup needs much more explanation and the decategorification, Morita equivalence and affine morphisms are some of the points which are subtly involved, plus kind of questions I asked at point of a topos. -
- CommentRowNumber3.
- CommentAuthorzskoda
- CommentTimeNov 19th 2009
I wrote an answer (more questions) to Mike and others in a query in point of a topos. I am interested in abelian categories there, not topoi but some proofs and reasonings should be analogous. -
- CommentRowNumber4.
- CommentAuthorMike Shulman
- CommentTimeNov 19th 2009
The discussion there is getting very off-topic; maybe it should be moved somewhere else. I don't really understand your last question, Zoran, but it seems to involve lots of specifics that don't have much to do with the general notion.
-
- CommentRowNumber5.
- CommentAuthorzskoda
- CommentTimeNov 19th 2009
- (edited Nov 19th 2009)
I first need the answer for the topos case: you said not in general, I know, but what about the topos of sheaves over a genuine topological space ? Where or what is a proof ?
The things which look to you specific are actually very general, most technical conditions are put just to have the factorization of affiness plus easy criteria for descent. You can imagine ANY category of categories with geometric like morphisms, any subcategory equivalent to 1-category of local models, gluing from reflective subcategories and the same question: can we glue representable objects into sets...
Grothendieck wrote once that his definition of abelian category in Tohoku was in fact motivated by thinking of categories of sheaves, so for him abelian category and topos are just two variants of the same notion, as well as corresponding reconstruction theorems and the rest. So I do not think it is off-topic.
I am confused with you saying that you do not understand the very question. You asked what specifics on T I should assume in order to ask wheather the geometric functors into it (from a local model) make a set. So I am asking the same question just the local model i snot just a SINGLE point (like the category SET) but any member of the subcategory equivalent to Aff. -
- CommentRowNumber6.
- CommentAuthorzskoda
- CommentTimeNov 19th 2009
- (edited Nov 19th 2009)
Here is an attempt for an example in Topoi but I am not sure if it is. Take the category Top of topological spaces. Then topological stacks are 1-stacks with some representability conditions; in particular they have an atlas by usual topological space. Now I do not know, but I suppose that the category of sheaves on a topological stack is still an elementary topos, though maybe not Grothendieck topos. Now is it true that if I take
[Sh(X),Sh(Y)]geom
where X is any topological space and Y a topological stack, then is this category equivalent to a set? -
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeNov 19th 2009
Specific or general, you used a lot of words that I don't understand and don't have time to understand. It wasn't at all clear to me that what I was being asked was about morphisms between topological spaces. A proof of that can be found at geometric morphism, although not dealing with the question of geometric transformations; the whole thing is in the Elephant, C1.4.5. In some context other than topological spaces, someone who understands that particular context (i.e. not me) would be better equipped to do a proof.
-
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeNov 19th 2009
- (edited Nov 19th 2009)
I moved the ongoing discussion from point of a topos to discussion from point of a topos (zoranskoda).
While the points of topoi are geom morphisms from Set, and Set is good enough to probe topological spaces, because they are made out of points, could not there be a more general statement that if one takes generalized S-points for S in some sub-2-category MODELS of Topoi which is equivalent to some 1-category, and if we look at topoi which are sheaf on some class of (charted) STACKS on MODELS
(I want in the sense of gluing localization but to start with maybe gluing in Grothendieck topology is good starter)
are the S-points for all S in MODELS enough in 1-categorical sense ?
I said earlier topological stacks (see my example one entry above which is probably overlooked) now "charted stacks" not just 1-stacks in usual sense because I need atlas to make sense of the category of sheaves on the stack.
Mike, thank for the reference, but I now see that the proof as it is is useless for generalizing to stacks (or more generally glued categories from representables, even when the gluing is via localizations). Unless one somehow uses generalized points in a way which is similar enough. This is so general and clean problem, I am sorry I confuse you with specific example but it is difficult to say it without any assumptions, as I see similar cases when it is clearly not true. Main trouble leading me to such complications is that the geometric morphisms are span-like while I need arrow-like ones. In some cases every bimodule/span is a true morphism. -
- CommentRowNumber9.
- CommentAuthorMike Shulman
- CommentTimeNov 19th 2009
Okay, I think I understand the question better now.
The only question about whether sheaves on a topological stack is a topos is about size, right, because Top is large? If Top were a small category then so would any (small) stack be, and hence sheaves on such a stack would again be a Grothendieck topos. It seems fairly likely to me that the representability conditions on a topological stack would ensure that sheaves on it are equivalent to sheaves on some small site and hence a Grothendieck topos. I'd be pretty surprised if one could show that it was an elementary topos without showing that it's a Grothendieck topos.
I'm also pretty sure that geometric morphisms into sheaves on a topological stack will not, in general, be equivalent to a set, because the whole point of stacks is that they have automorphisms. For instance, I can consider some topological stacks presented by topological groupoids (i.e. internal groupoids in Top), and then every topological natural transformation between topological functors should induce a geometric transformation between corresponding topoi.
Can every topological stack be presented by a topological groupoid? If so, then there's a standard way to get a Grothendieck topos from a topological groupoid using equivariant sheaves, which seems like in good cases it would agree with sheaves on the stack in the other sense.
-
- CommentRowNumber10.
- CommentAuthorGuest
- CommentTimeNov 19th 2009
The whole idea of topological stacks is that they are all 'presentable' by topological groupoids. Just how nice you want the theory of such stacks to be determines how restrictive you make the presentability. Eg For artin stacks you need a representable etale map from a topological space - the cech groupoid of this in the 2-cat of stacks is then representable by a topological groupoid. Unlike cech groupoids in Top, this will have nontrivial automorphisms.
Got to run, hope this helps
David Roberts -
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeNov 19th 2009
- (edited Nov 19th 2009)
<blockquote> A proof of that can be found at <a href="https://ncatlab.org/nlab/show/geometric+morphism">geometric morphism</a>, although not dealing with the question of geometric transformations; the whole thing is in the Elephant, C1.4.5. </blockquote> <p>Zoran, do you have the Elephant in reach at the moment? I don't I should look in the library today. About time that I start reading that book.</p> <p>I suppose -- given the the proof at <a href="https://ncatlab.org/nlab/show/geometric+morphism">geometric morphism</a> which says that the geometric morphisms between localic toposes are as a set already in bijection with the set of continuous maps -- that there are no nontrivial natural transformations between these geometric morphisms in the first place.</p> <p>This is the type of statement (if not its exact version) that I believe you want in your setup.</p> <p>By the way, I'd be very interested in having an nLab page that discusses the similarity, as far as it goes, between</p> <p>toposes <-> abelian categories</p> <p>and then</p> <p>(oo,1)-toposes <-> stable (oo,1)-categories .</p> <p>I just don't feel that I understand this well enough myself to start such a page myself.</p> -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeNov 19th 2009
<div> <p>Well, I still find <a href="http://www.noncommutative.org/#comment-92">David Ben-Zvi's message</a> seems to point in a useful direction.</p> <blockquote> Urs, The idea that categories of quasicoherent sheaves are analogs of topoi is certainly implicit in noncommutative algebraic geometry, but I don’t know where it’s explicit. However I wouldn’t say that one is a special case of the other, rather that one is a linearization of the other. Namely, rather than assigning to an algebra (or a scheme) the (oo-)category of sheaves of sets (or spaces) over it, such as those represented by other algebras, we are linearizing/stabilizing/Goodwillie-differentiating this assignment and considering sheaves of modules instead. Thus while of course you’re right that stable (oo,1)-categories are special cases of oo-topoi, the usual functor from schemes to the former is not the same as the usual functor to the latter, but rather is its stabilization. A related point is that in my (highly unoriginal) view, NAG is not about algebras, but about these (oo-)categories of modules (ie algebras up to Morita equivalence) , so for example it seems misleading to me to look for topologies on the category of algebras, rather than on some category or 2-category of categories (say the oo-category of stable presentable oo-categories) in order to formulate NAG (though far smarter people disagree). (In particular I don’t see why non-accessible categories are relevant?) It’s also nice to note that most common categories are derived equivalent to modules over a (derived) algebra, so the difference mentioned in that n-lab page between NC algebraic geometry and NC topology is less pronounced in the derived setting. </blockquote> <p>Concerning the second bit: that's currently what you are talking about, Zoran, right? Replacing the site of algebras^op by a 2-cat of A-oo-categories?</p> </div> -
- CommentRowNumber13.
- CommentAuthorMike Shulman
- CommentTimeNov 19th 2009
I suppose -- given the the proof at geometric morphism which says that the geometric morphisms between localic toposes are as a set already in bijection with the set of continuous maps -- that there are no nontrivial natural transformations between these geometric morphisms in the first place.
If the space is separated enough, yes. But actually,
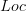 and
and 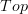 are (1,2)-categories via the specialization order, and it's that (1,2)-category
are (1,2)-categories via the specialization order, and it's that (1,2)-category 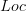 that's equivalent to a full sub-2-category of
that's equivalent to a full sub-2-category of 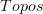 .
. -
- CommentRowNumber14.
- CommentAuthorzskoda
- CommentTimeNov 19th 2009
Sorry did not look at Urs's comments yet today. Yes I agree with ben Zvi that usual (=nonderived) NAG should be formulated in 2-categorical setup, but I slightly disagree that this is up to Morita equivalence, as if one works over a base scheme, then Morita equivalences can be ruled out. As I do not work in derived setup here, no A infty but rather abelian categories with or without distinguished object. -
- CommentRowNumber15.
- CommentAuthorIngoBlechschmidt
- CommentTimeOct 3rd 2015
Added to point of a topos two small previously missing assumptions: For geometric morphisms to bijectively correspond to continuous maps , one needs that is sober; and for a Grothendieck topos to admit a geometric surjection from a topos of the form , one needs that has enough points.
-
- CommentRowNumber16.
- CommentAuthorMike Shulman
- CommentTimeOct 4th 2015
Thanks! For the first, wouldn’t it be better to talk about locales?
-
- CommentRowNumber17.
- CommentAuthorIngoBlechschmidt
- CommentTimeOct 4th 2015
Well, yes; but I think that pedagogically, it’s still nice to have the details spelled out in the context of topological spaces (as in the current form of the entry). I added the following comment:
“Note that the observation that the points of are in bijection with the points of actually factors over an intermediate concept, namely that of points of a locale. Firstly, any topological space gives rise to a locale; if the space is sober, its points are in bijection with the locale-theoretic points of the induced locale. Secondly, for any locale (spatial or not), its locale-theoretic points correspond to the points of its induced sheaf topos.”
-
- CommentRowNumber18.
- CommentAuthorMike Shulman
- CommentTimeOct 5th 2015
Thanks, that sounds great.
-
- CommentRowNumber19.
- CommentAuthorOscar_Cunningham
- CommentTimeFeb 23rd 2018
In the section “In sheaf toposes” what does “Con” in “ConFlatFunc” mean?
-
- CommentRowNumber20.
- CommentAuthorDavid_Corfield
- CommentTimeFeb 23rd 2018
Presumably continuous functor.
-
- CommentRowNumber21.
- CommentAuthorDavid_Corfield
- CommentTimeFeb 23rd 2018
A continuous functor, , in MacLane-Moerdijk (p. 384)means that it sends covering sieves to colimit diagrams.
-
- CommentRowNumber22.
- CommentAuthorMike Shulman
- CommentTimeFeb 23rd 2018
Maybe it would be clearer to write instead of .
-
- CommentRowNumber23.
- CommentAuthorDavid_Corfield
- CommentTimeFeb 23rd 2018
Probably also need a reference to the warning at continuous functor.
-
- CommentRowNumber24.
- CommentAuthorOscar_Cunningham
- CommentTimeFeb 23rd 2018
I edited it to:
In sheaf toposes
The following characterization of points in sheaf toposes a special case of the general statements at morphism of sites.
Proposition 2.2
For a site, there is an equivalence of categories
(Morphisms of sites are precisely the continuous flat functors.)
This appears for instance as (MacLaneMoerdijk, corollary VII.5.4).
Where “continuous” links to cover-preserving functor.
-
- CommentRowNumber25.
- CommentAuthorThomas Holder
- CommentTimeOct 7th 2020
1 to 25 of 25