nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeNov 20th 2009
I tried at locally presentable category to incorporate the upshot of the query box discussions into the text, then moved the query boxes to the bottom
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeNov 24th 2009
- (edited Nov 24th 2009)
I added to small object a section Details with a discussion of how homs out of X commuting with colimits is equivalent to morphisms from X into a colimit having lifts to one of the component objects.
Then I added a section Properties where I want to deduce from this that hence every small object is
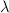 -small for every sufficiently large regular cardinal
-small for every sufficiently large regular cardinal 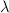 .
.Help!
This seems obvious enough, but I feel like I am missing the fully formal way to say this. For instance the fact that
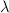 be regular must be important, but I am not sure exactly how that goes into the argument. Must be something about colimits over regular-
be regular must be important, but I am not sure exactly how that goes into the argument. Must be something about colimits over regular-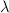 -filtered diagrams being computable as colimits over sub-diagrams of colimits. But I keep feeling unsure about this.
-filtered diagrams being computable as colimits over sub-diagrams of colimits. But I keep feeling unsure about this. -
- CommentRowNumber3.
- CommentAuthorMike Shulman
- CommentTimeNov 25th 2009
Actually, it's simpler than that. I added the proof to small object.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeNov 25th 2009
Thanks, Mike,now that's indeed obvious enough.
I started adding a section listing examples at locally small category. But this should eventually be extended.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeNov 25th 2009
added to accessible category a sentence on how that relates to locally presentable category -- hope I got that right
-
- CommentRowNumber6.
- CommentAuthorMike Shulman
- CommentTimeNov 25th 2009
Minor correction: I think every accessible category is locally small.
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeNov 26th 2009
fleshed out the material at locally presentable category a bit more
made the distinction between locally presentable and locally kappa-presentable
added more details to the simple example of Set as locally
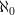 -presentable.
-presentable.
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeApr 15th 2010
added to the list of equivalent definitions at locally presentable category the characterization as reflective subcategories of presheaf categories.
-
- CommentRowNumber9.
- CommentAuthorMike Shulman
- CommentTimeApr 15th 2010
That’s only an equivalent definition if you also assume the category to be closed under -filtered colimits, although of course what you wrote didn’t claim that it was. I modified the statement to make this clear.
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeApr 15th 2010
Mike, thanks, I may actually be mixed up about this. I guess the point is that I should be talking about accessible localizations where I have so far been talking (and thinking) about just localizations.
I’ll look into it now…
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeApr 15th 2010
Mike,
I have edited your edit further now by mentioning that this means that the embedding functor is an accessible functor. Hope I got it right.
1 to 11 of 11