Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory object of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: left Bousfield localization of model categories

Bottom of Page

1 to 24 of 24

  1.  
    • CommentRowNumber1.
    • CommentAuthorUrs
    • CommentTimeNov 25th 2009
    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeNov 26th 2009

    I completed the existece proof with the bit showing the accessibility of the S-local weak equivalences.

    Then I added a section prerequisite for the proof that lists briefly all the material at other entries, previously just having been linked to, that enters the proof.

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeNov 26th 2009
    • (edited Nov 26th 2009)

    Based on some feedback that I got behind the scenes, I have now rearranged the material, to make it more light-weight at the beginning.

    • the section Properties now has the central properties one can deduce for a Bousfield localization that do not require combinatorial model category technology

    • the section Existence of ... has the existence result for the combinatorial case pretty much as before, but minus the material that has been moved to "Properties"

    • and the Definition section is now such that it downplays the "derived hom" 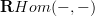\mathbf{R}Hom(-,-) and instead tends to arrange things such that they are properly cofibrant or fibrant . Because it was suggested to me that invoking the derived hom concept makes this look, to the non-expert reader- much more arcane than it is.

    I just hope that the interconnecting logic between the paragraphs is now still consistent. I fddled a bit with adjusting the statements to the slightly changed assimptions.

    • CommentRowNumber4.
    • CommentAuthorUrs
    • CommentTimeApr 15th 2012

    added the statement that left Bousfield localization is functorial with respect to Quillen equivalences, here.

    • CommentRowNumber5.
    • CommentAuthorUrs
    • CommentTimeMar 17th 2017
    • (edited Mar 17th 2017)

    I have added statement and proof (here) that given a left Bousfield localization, then local fibrations between local objects are global fibrations.

    (I am assuming functorial factorization, which is of course provided under the generic assumption of the entry that we are localizing a cofibrantly generated model category. But probably one can get the statement more generally.)

    • CommentRowNumber6.
    • CommentAuthorUrs
    • CommentTimeMar 17th 2017
    • (edited Mar 17th 2017)

    I have made more explicit statement and proof that functorial fibrant replacement in a left Bousfield localized model category is a model for the derived adjunction unit, here

    • CommentRowNumber7.
    • CommentAuthorUrs
    • CommentTimeApr 19th 2023

    added pointer to:

    diff, v60, current

    • CommentRowNumber8.
    • CommentAuthorUrs
    • CommentTimeApr 21st 2023

    in the statement of Smith’s theorem in the entry (here) we are assuming simplicial enrichment.

    Barwick here states Smith’s theorem without that assumption, it seems. Or does he?

    • CommentRowNumber9.
    • CommentAuthorDmitri Pavlov
    • CommentTimeApr 21st 2023

    (Answered #8 in the other thread.)

    • CommentRowNumber10.
    • CommentAuthorDmitri Pavlov
    • CommentTimeApr 21st 2023

    Completely rewrote the “Idea” section.

    Deleted unnecessary assumptions: the model category need not be simplicial, morphisms need not be cofibrations with cofibrant domains, an SS-local object need not be fibrant, an SS-local weak equivalence need not be a cofibration.

    diff, v65, current

    • CommentRowNumber11.
    • CommentAuthorDmitri Pavlov
    • CommentTimeApr 21st 2023

    Rewrote many sections.

    diff, v65, current

    • CommentRowNumber12.
    • CommentAuthorDmitri Pavlov
    • CommentTimeApr 21st 2023

    Tried to make the connection to reflective subcategories much more prominent.

    diff, v65, current

    • CommentRowNumber13.
    • CommentAuthorUrs
    • CommentTimeApr 21st 2023
    • (edited Apr 21st 2023)

    Great. Thanks for looking into it.

    But let’s add references for the claims. On the non-simplicial combinatorial case, is there a reference beyond Barwick’s unpublished preprint?

    • CommentRowNumber14.
    • CommentAuthorDmitri Pavlov
    • CommentTimeApr 21st 2023

    is there a reference beyond Barwick’s unpublished preprint?

    Barwick’s paper has been published many years ago. I already added a reference in the previous revision.

    • CommentRowNumber15.
    • CommentAuthorUrs
    • CommentTimeApr 22nd 2023

    I see. Thanks!

    • CommentRowNumber16.
    • CommentAuthorUrs
    • CommentTimeApr 22nd 2023
    • (edited Apr 22nd 2023)

    I have made explicit (here) that the published version of Barwick’s article has a different title than the arXiv version.

    In fact, also the Theorem-numbers are different, and I have now tried to adjust this in the text where they are being referenced.

    [edit: this may need further attention. But I am in a rush now to get to an airport…]

    Finally, I deleted the now duplicated previous item listing just the arXiv version.

    diff, v67, current

    • CommentRowNumber17.
    • CommentAuthorUrs
    • CommentTimeApr 22nd 2023
    • (edited Apr 22nd 2023)

    added pointer to:

    diff, v67, current

    • CommentRowNumber18.
    • CommentAuthorDmitri Pavlov
    • CommentTimeApr 22nd 2023
    • (edited Apr 22nd 2023)

    Re #16:

    Barwick’s paper “On left and right…” is a fusion of his three arXiv preprints from August 2007:

    Section 3: On Reedy Model Categories

    Section 4: On (Enriched) Left Bousfield Localization of Model Categories

    Section 5: On the Dreaded Right Bousfield Localization

    Currently, the article also cites the last paper separately, but it is incorporated as Section 5.

    • CommentRowNumber19.
    • CommentAuthorUrs
    • CommentTimeApr 22nd 2023

    Thanks. I see. So I have added all three here.

    (about to board now, will be offline soon…)

    diff, v70, current

    • CommentRowNumber20.
    • CommentAuthorUrs
    • CommentTimeApr 23rd 2023

    added pointer to:

    diff, v71, current

    • CommentRowNumber21.
    • CommentAuthorUrs
    • CommentTimeApr 26th 2023

    For completeness I made a References-subsection “Monoidal case” (here), currwntly just duplicating the references earlier added at monoidal localiztion

    diff, v73, current

    • CommentRowNumber22.
    • CommentAuthorDmitri Pavlov
    • CommentTimeApr 26th 2023

    Re #21: After Barwick, the earliest reference for monoidality of left Bousfield localizations is https://arxiv.org/abs/0907.0730v4, Lemma 28.

    • CommentRowNumber23.
    • CommentAuthorUrs
    • CommentTimeApr 26th 2023

    Thanks. Have added it here.

    diff, v73, current

    • CommentRowNumber24.
    • CommentAuthorDmitri Pavlov
    • CommentTimeDec 28th 2023

    Renaming to “left Bousfield localization of model categories”, since the article makes no mention of right Bousfield localizations, othen than two sentences that say it’s analogous.

    Will create a separate article on right Bousfield localizations.

    diff, v75, current

1 to 24 of 24

  1.