nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeNov 25th 2009
finished typing part 1) and 2) of the proof of the existence theorem at Bousfield localization of model categories
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeNov 26th 2009
I completed the existece proof with the bit showing the accessibility of the S-local weak equivalences.
Then I added a section prerequisite for the proof that lists briefly all the material at other entries, previously just having been linked to, that enters the proof.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeNov 26th 2009
- (edited Nov 26th 2009)
Based on some feedback that I got behind the scenes, I have now rearranged the material, to make it more light-weight at the beginning.
the section Properties now has the central properties one can deduce for a Bousfield localization that do not require combinatorial model category technology
the section Existence of ... has the existence result for the combinatorial case pretty much as before, but minus the material that has been moved to "Properties"
and the Definition section is now such that it downplays the "derived hom"
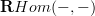 and instead tends to arrange things such that they are properly cofibrant or fibrant . Because it was suggested to me that invoking the derived hom concept makes this look, to the non-expert reader- much more arcane than it is.
and instead tends to arrange things such that they are properly cofibrant or fibrant . Because it was suggested to me that invoking the derived hom concept makes this look, to the non-expert reader- much more arcane than it is.
I just hope that the interconnecting logic between the paragraphs is now still consistent. I fddled a bit with adjusting the statements to the slightly changed assimptions.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeApr 15th 2012
added the statement that left Bousfield localization is functorial with respect to Quillen equivalences, here.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeMar 17th 2017
- (edited Mar 17th 2017)
I have added statement and proof (here) that given a left Bousfield localization, then local fibrations between local objects are global fibrations.
(I am assuming functorial factorization, which is of course provided under the generic assumption of the entry that we are localizing a cofibrantly generated model category. But probably one can get the statement more generally.)
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeMar 17th 2017
- (edited Mar 17th 2017)
I have made more explicit statement and proof that functorial fibrant replacement in a left Bousfield localized model category is a model for the derived adjunction unit, here
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeApr 19th 2023
added pointer to:
- Tyler Lawson, An introduction to Bousfield localization [arXiv:2002.03888]
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeApr 21st 2023
-
- CommentRowNumber9.
- CommentAuthorDmitri Pavlov
- CommentTimeApr 21st 2023
(Answered #8 in the other thread.)
-
- CommentRowNumber10.
- CommentAuthorDmitri Pavlov
- CommentTimeApr 21st 2023
-
- CommentRowNumber11.
- CommentAuthorDmitri Pavlov
- CommentTimeApr 21st 2023
-
- CommentRowNumber12.
- CommentAuthorDmitri Pavlov
- CommentTimeApr 21st 2023
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeApr 21st 2023
- (edited Apr 21st 2023)
Great. Thanks for looking into it.
But let’s add references for the claims. On the non-simplicial combinatorial case, is there a reference beyond Barwick’s unpublished preprint?
-
- CommentRowNumber14.
- CommentAuthorDmitri Pavlov
- CommentTimeApr 21st 2023
is there a reference beyond Barwick’s unpublished preprint?
Barwick’s paper has been published many years ago. I already added a reference in the previous revision.
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeApr 22nd 2023
I see. Thanks!
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeApr 22nd 2023
- (edited Apr 22nd 2023)
I have made explicit (here) that the published version of Barwick’s article has a different title than the arXiv version.
In fact, also the Theorem-numbers are different, and I have now tried to adjust this in the text where they are being referenced.
[edit: this may need further attention. But I am in a rush now to get to an airport…]
Finally, I deleted the now duplicated previous item listing just the arXiv version.
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeApr 22nd 2023
- (edited Apr 22nd 2023)
added pointer to:
- Tibor Beke, Th, 1.7, Prop. 1.15, 1.19 in: Sheafifiable homotopy model categories, Math. Proc. Cambridge Philos. Soc. 129 3 (2000) 447-475 [arXiv:math/0102087, doi:10.1017/S0305004100004722]
-
- CommentRowNumber18.
- CommentAuthorDmitri Pavlov
- CommentTimeApr 22nd 2023
- (edited Apr 22nd 2023)
Re #16:
Barwick’s paper “On left and right…” is a fusion of his three arXiv preprints from August 2007:
Section 3: On Reedy Model Categories
Section 4: On (Enriched) Left Bousfield Localization of Model Categories
Section 5: On the Dreaded Right Bousfield Localization
Currently, the article also cites the last paper separately, but it is incorporated as Section 5.
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeApr 22nd 2023
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeApr 23rd 2023
added pointer to:
- Luca Pol, Jordan Williamson, The Left Localization Principle, completions, and cofree -spectra, J. Pure Appl. Algebra 224 11 (2020) 106408 [arXiv:1910.01410, doi:10.1016/j.jpaa.2020.106408]
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeApr 26th 2023
For completeness I made a References-subsection “Monoidal case” (here), currwntly just duplicating the references earlier added at monoidal localiztion
-
- CommentRowNumber22.
- CommentAuthorDmitri Pavlov
- CommentTimeApr 26th 2023
Re #21: After Barwick, the earliest reference for monoidality of left Bousfield localizations is https://arxiv.org/abs/0907.0730v4, Lemma 28.
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeApr 26th 2023
-
- CommentRowNumber24.
- CommentAuthorDmitri Pavlov
- CommentTimeDec 28th 2023
1 to 24 of 24