nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorbwebster
- CommentTimeDec 2nd 2009
Taking the advice that if I write something on the internet, it should be stuck on the n-Lab, I've converted my recent comments in the n-category cafe and some old blog posts into a new page on the relationship between categorification and groupoidification: categorification via groupoid schemes
-
- CommentRowNumber2.
- CommentAuthorGuest
- CommentTimeDec 2nd 2009
Comments at categorification via groupoid schemes on terminology and notation for the first paragraph.
David Roberts -
- CommentRowNumber3.
- CommentAuthorbwebster
- CommentTimeDec 2nd 2009
Ok, I think I've addressed your questions, so I deleted the query box. Thanks, by the way; I'm sure the notation is still ghastly, but somehow the work "nerve" had slipped from my mind, and I didn't know about \rightrightarrows.
-
- CommentRowNumber4.
- CommentAuthorbwebster
- CommentTimeDec 2nd 2009
Oh, the one part I was a bit unsure of is the question about a "groupoid of fintie sets" I meant a groupoid whose arrows and morphisms are finite, with no additional structure. Does "a groupoid of finite sets" mean something other than that?
-
- CommentRowNumber5.
- CommentAuthorGuest
- CommentTimeDec 2nd 2009
I was thinking it could be interpreted as a groupoid whose objects are finite sets, say those arising as the F_q points of a scheme.
David Roberts -
- CommentRowNumber6.
- CommentAuthorGuest
- CommentTimeDec 2nd 2009
I changed the first dotpoint to read 'finite groupoid', since that means the same thing as groupoid in FinSet
David Roberts -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeDec 2nd 2009
Thanks for this entry!
I edited it a bit (made the Theorem environment say "Theorem") and added some further links, for instance to motive.
One question: you write "the motive of
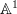 " is pulling up through the projection
" is pulling up through the projection 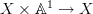 and then pushing down along it again.
and then pushing down along it again.What is the terminology here: is this operation itself called a motive?
(All I know about motives comes from a very superficial encounter with Voevodsky's lecture notes.)
-
- CommentRowNumber8.
- CommentAuthorbwebster
- CommentTimeDec 2nd 2009
yeah, I decided it would probably be better to call that "multiplication by the motivic integral of $\mathbb{A}^1$."
-
- CommentRowNumber9.
- CommentAuthorzskoda
- CommentTimeApr 7th 2010
- (edited Apr 7th 2010)
As groupoidification appeared today again on the cafe, I have updated links, including the sbseminar links at Hecke algebra. I wish we had also a meaningful entry on Hall algebra but I am running out of time with so many things on the plate and other important deadlines approaching by this weekend.
We should also understand the general connection between the motivic functions and groupoidification.
-
- CommentRowNumber10.
- CommentAuthorbwebster
- CommentTimeMay 2nd 2010
Zoran, I'm not sure I understand what general connection you have in mind. I guess I tend to think of such a connection as factoring through the realization functor from motives to Galois representations, and thus going through well-understood mathematics.
1 to 10 of 10