nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeDec 15th 2009
- (edited Dec 15th 2009)
created a section Contractible objects at lined topos.
This introduces and discusses a bit a notion of objects being contractible with respect to a specified line object (maybe the section deserves to be at interval object instead, not sure).
This notion is something I made up, so review critically. I am open for suggestions of different terminology. The concept itself, simple as it is (though not entirely trivial), I need for the discussion of path oo-groupoids of oo-stacks on my personal web:
if a lined Grothendieck topos
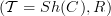 is such that all representable objects are contractible with respect to the line object
is such that all representable objects are contractible with respect to the line object 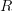 , then the path oo-groupoid functor
, then the path oo-groupoid functor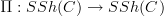
on simplicial sheaves, which a priori is only a Qulillen functor of oo-prestacks, enhances to a Quillen functor of oo-stacks (i.e. respects the local weak equivalences).
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeDec 15th 2009
<div> <blockquote> if a lined Grothendieck topos is such that all representable objects are contractible with respect to the line object R, then the path oo-groupoid functor on simplicial sheaves, which a priori is only a Qulillen functor of oo-prestacks, enhances to a Quillen functor of oo-stacks </blockquote> <p>The proof for that, by the way, is now typed up in the section <a href="http://ncatlab.org/schreiber/show/path+%E2%88%9E-groupoid#the_local_quillen_adjunction_13">Local Quillen adjunction</a> at <a href="http://ncatlab.org/schreiber/show/path+%E2%88%9E-groupoid">path oo-groupoid</a> on my personal web.</p> </div> -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeDec 22nd 2009
added one more example at lined topos in the section Contractible objects: on contractible objects in smooth toposes
1 to 3 of 3