nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeDec 30th 2009
I expanded derivation a little:
gave the full definition with values in bimodules and added to the examples a tiny little bit on examples for this case.
I think I also corrected a mistake in the original version of the definition: the morphism
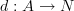 is of course not required to be a module homomorphism (well, it is, but over the underlying ground ring, not over
is of course not required to be a module homomorphism (well, it is, but over the underlying ground ring, not over  ).
).At Kähler differential I just polished slightly, adding a few words and links in the definition and adding sections. I don't really have time for this derivations/Kähler stuff at the moment. Am hoping that those actively talki9ng about this on the blog will find the time to archive their stable insights at this entry.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeDec 30th 2009
- (edited Dec 30th 2009)
I want to make contact between the discussion at Kähler differential and Weil algebra and discuss how both relate to mapping cones in
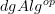 .
.I started polishing and expanding the Idea section at Weil algebra accordingly, but will have to interrupt now and continue in a little while.
-
- CommentRowNumber3.
- CommentAuthorJohn Baez
- CommentTimeJan 3rd 2010
I added a lot of material to Kaehler differential, so now I think most of the insights from the n-Cafe are here in polished form.
Not, however, the proof that all derivations of smooth functions on the real line come from vector fields! That's in week287 of This Week's Finds. -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeJan 3rd 2010
Thanks John. I wish I had more time at the moment to add to this.
One remark I still want to add is this: the crucial fact which you keep emphasizing, that every smooth function on the line may be expanded as
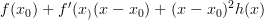 for
for 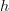 smooth is the crucial fact that makes the standard Models for Smooth Infinitesimal Analysis tick, because this means that the ring of dual numbers
smooth is the crucial fact that makes the standard Models for Smooth Infinitesimal Analysis tick, because this means that the ring of dual numbers 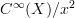 makes sense also for smooth functions.
makes sense also for smooth functions. -
- CommentRowNumber5.
- CommentAuthorzskoda
- CommentTimeJan 3rd 2010
The treatment is still 1-categorical and not n-categorical. I started at some point an entry on cotangent complex, which gives the correct derived notion/perspective, putting the references, but I need much time or help of others to continue.
-
- CommentRowNumber6.
- CommentAuthorJohn Baez
- CommentTimeJan 3rd 2010
I don't understand the models for smooth infinitesimal analysis very well. But, what Urs calls the "crucial fact" is directly related to Anders Kock's concept of a Fermat theory. In a Fermat theory we can write f(x) = f(xo) + g(x)(x - xo), and then we can iterate to get the formula Urs wrote. So, clearly Kock understands how this idea is related to smooth infinitesimal analysis.
1 to 6 of 6