nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 4th 2010
I am starting Deformation Theory
in the course of this I so far added links and an extra secton to Kähler differential and links to and from cotangent complex.
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeJan 4th 2010
Great, my call for help in that department has met understanding. :)
BTW, I added to subobject a section describing the functorial aspect of taking the set of subobject(s).
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 4th 2010
wrote section Modules, derivations, Kähler differentials at deformation theory
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeJan 4th 2010
created tangent (infinity,1)-category
funny, so what i was missing back when I talked about tangent categories is that the fibers have to be stabilized for things to fit together...
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeJan 4th 2010
started an Idea-section at cotangent complex (but incomplete)
Zoran, could you have a look and see how this harmonizes with the existing Motivation-section, which I guess you wrote? Feel free to reorganize the Idea section that I just added.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeJan 4th 2010
created a section Generalization to arbitrary (oo,1)-category at derivation.
-
- CommentRowNumber7.
- CommentAuthorzskoda
- CommentTimeJan 4th 2010
What you wrote is of course nice. The emphasis which I put is from the motivation point of view. One is not having infty-categories to start with but has problems with nontrivial automorphisms, which infinitesimally correspond to derivations. The obstructions are seen at cohomologies and the correct version to see all is via looking what is the representing object in a derived setting. This is the thought which in various forms existed from 1960s, works of Illusie and through the references I quoted and many others. It is correct as you pointed out to see those as infty-categorification of Kahler differentials, but I think the practical mathematicians prefer not to think of this as an ANALOGUE in higher setup but as a correct version, when the conditions are not the best. In the best smooth situations, Kahler differentials are enough. I am not sure how to say to include both points of view: if one starts with derived geometry at the beginning one has the point of view which you emphasise; when one starts with practical question, extension to derived world comes only to the extent which is necessary. Uglier the problem is more is the need to define all parts of the story in derived setup. I will have to read more to remind yourself these days. Today there was some political turmoil in Croatia (which ended well) so I was distracted for few hours and gave no contribution in timely fashion to your very successful effort. Thanks!
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeJan 5th 2010
Now a crucial question is:
is a tangent (infinity,1)-category
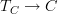 still a bifibration.
still a bifibration.It should be. Notice that this would then be the answer to a bunch of questions that I scattared across several pages:
I was looking for the definition of Ben-Zvi's geometric infinity-function theory that would work over arbitrary sites. Ben-Zvi uses the bifibration
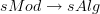 and works over the site of simplicial algebras, hence with algebraic derived oo-stacks.
and works over the site of simplicial algebras, hence with algebraic derived oo-stacks.What is the analog of this over arbitrary sites, such that over the point it reprduces John's "groupoidification"?
At geometric function object I discuss how John's groupoidification is realy the geometric oo-function theory for the codomain fibration. But it wasn't clear to me how that systematically connects to
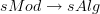 .
.Now I know. By Lurie's results, it should be true that
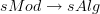 is the codomain fibration over
is the codomain fibration over 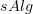 , but fiberwise stabilized.
, but fiberwise stabilized.Hm, now I wonder if this fiberwise stabilization applied to John's setup wouldn't solve the linearization problem encountered there.
That must be it. Hypothesis: given any oo-stack oo-topos
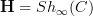 on some site
on some site 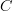 , there is an
, there is an 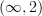 -stack
-stack 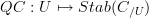 whose classified cartesian fibration is in fact a bifibration, and the geometric oo-function theory of
whose classified cartesian fibration is in fact a bifibration, and the geometric oo-function theory of 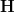 is the pull-push of
is the pull-push of 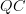 through spans in
through spans in 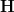 .
.For the case
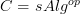 this yieldf Ben-Zvi et al's theory.
this yieldf Ben-Zvi et al's theory.For the case
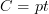 this yields an oo-version of Baez-Dolan "groupoidification" that automatically takes care of the linearization and rationalization.
this yields an oo-version of Baez-Dolan "groupoidification" that automatically takes care of the linearization and rationalization.For notice that under groupoid cardinality an oo-groupoid
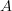 is a series
is a series 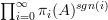 , similarly for a spectrum it should be
, similarly for a spectrum it should be 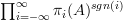 . Or possibly we can drop the stabilization for the Baez-Dolan picture.
. Or possibly we can drop the stabilization for the Baez-Dolan picture. -
- CommentRowNumber9.
- CommentAuthorzskoda
- CommentTimeJan 5th 2010
- (edited Nov 29th 2011)
This bifibration claim bothered me yesterday, before your post. But you obviously have more grasp there.
I will add some material about cotangent complex from more classical point of view. I think we should emphasise that the trivial (i.e. square zero) extensions of R (even in noncommutative case!!) are nothing but the abelian group objects of the slice category Ring/R. This fact extends to other cases, like when one looks at Lie algebras instead of rings, and I suspect though I do not know the reference that it holds for algebras over a given quadratic operad.
Quillen defined the cotangent complex as a derived functor, this perspective is more understandable for practical mathematician than the full setup of quasicategories. The modern phrasing of th derived point of view (which according to the Lurie is essentially the same what he wrote) is in the paper of Schwede (toward the end of the article) which is quoted in the references at cotangent complex.
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeJan 5th 2010
following public request, I added now a fairly detailed expositional beginning in the Idea section at deformation theory
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeJan 5th 2010
<div> <blockquote> Quillen defined the cotangent complex as a derived functor, this perspective is more understandable for practical mathematician than the full setup of quasicategories. The modern phrasing of th derived point of view (which according to the Lurie is essentially the same what he wrote) is in the paper of Schwede (toward the end of the article) which is quoted in the references at deformation theory. </blockquote> <p>Thanks, that's good. We should add this.</p> </div> -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeJan 5th 2010
added paragraph nPOV: In deformation theory to nPOV.
I notice that David Corfield has meanwhile added something to nPOV: In logic
-
- CommentRowNumber13.
- CommentAuthorzskoda
- CommentTimeJan 5th 2010
- (edited Jan 5th 2010)
Deformation theory studies the obstruction theory of extensions to infinitesimal thickenings.
No, not infinitesimal in general. Infinitesimal problem is the subject of formal deformation theory. Wheather the vanishing of formal obstructions gives an ACTUAL (finite) deformation is a special problem and a subject of many theorems (still within the deformation theory proper) when this is actually sufficient. In general one wants to extend a special fiber to a FAMILY which specialized at some point is isomorphic to the one at special fiber. Thus in general one wants to find a functor which will to every space X containing a special point x_0, assign a family A = A(X) such that at x_0 it specializes to A_0. Thus the basic object to find is the DEFORMATION FUNCTOR. Now, for some purposes, one restricts to deformation functors on infinitesimal families with lots of finiteness conditions (thus Artinian rings and alike). This is telling much about more general case, but sometimes it is not sufficient.
-
- CommentRowNumber14.
- CommentAuthorzskoda
- CommentTimeJan 5th 2010
- (edited Jan 5th 2010)
In deformation theory, section cotangent complex I placed the classical definition of the cotangent complex.
I also radically reorganized cotangent complex, placing the motivation first, then the classical definition and then the outline of higher (which was previous Idea section).
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
on request by Jim Stasheff, I added to deformation theory a link to a lecture by Yan Soibelman (at the very end of the entry)
-
- CommentRowNumber16.
- CommentAuthorDavid_Corfield
- CommentTimeJan 7th 2010
Have people seen Mazur's PERTURBATIONS, DEFORMATIONS, AND VARIATIONS (AND \NEAR-MISSES") IN GEOMETRY, PHYSICS, AND NUMBER THEORY? There could be some good ideas for the expositary part of deformation theory (which is already good!). -
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeJan 7th 2010
Haven't seen it. Please add the link to the entry.
I won't have time to add more to that entry at the moment. Maybe you do.
-
- CommentRowNumber18.
- CommentAuthorDavid_Corfield
- CommentTimeJan 7th 2010
Added a link and also to Doran's Deformation Theory: An Historical Annotated Bibliography. -
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
I added link to textbook by Kontsevich-Soibelman to deformation theory
I also created subsections for the References-section and tried to order the long list of references a bit by nature (lectures, textbooks, etc.) Zoran, please have a look.
-
- CommentRowNumber20.
- CommentAuthorzskoda
- CommentTimeJan 10th 2010
- (edited Jan 10th 2010)
I dislike the division into textbooks and further readings here. First of all Kontsevich Soibelman reference has rather many errors and it is very incomplete at present so it is far from such a standing. Second on the level of being basic some of the articles below are more basic. So I would vote for getting back the reference without that division. and I ll do it now.
I removed the subdivisons in bibilography. It was discuttable in other points as well. Some of the articles quoted as articles were also lectures and other way around etc. It is better not to make lager biases here. The references, authors and titles speak enough for themselves.
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeJan 10th 2010
Okay, maybe we can add at least some comments on the nature of the references. Such as which somebody entirely new to the topic should start with, and which provide more detailed points.
-
- CommentRowNumber22.
- CommentAuthorzskoda
- CommentTimeJan 11th 2010
- (edited Jan 11th 2010)
Each reference could always be annotated in short way, just I think dividing them in classes is discutable, specially because nobody among us read even superficially all of the listed references. The reference due Efimov, Lunts and Orlov is unique in the sense of giving bicategorical perspective on Artin deformation functors which were before always treated 1-categorically. Lunts told me that the difference is not just in precision but very essential for the right approach to the deformation theory.
I don't think there exist easy reference to start with deformation theory. There are naive treatement of easy examples like deformation of fin.dim. Lie or associative algebras done in many references but anything going further than explicit treatment of 2-3 examples tends to be hard and steep, not counting cheating references. I am keeping adding references which I consider good. I have a file from Artin himself, which is very good classical reference, but can not find online link.
-
- CommentRowNumber23.
- CommentAuthorzskoda
- CommentTimeJun 25th 2010
There is a section title Further categorification in the entry deformation theory with currently empty content.
-
- CommentRowNumber24.
- CommentAuthorKevin Lin
- CommentTimeJun 25th 2010
FYI, Lurie has a new paper on deformation theory: http://www.math.harvard.edu/~lurie/papers/moduli.pdf
-
- CommentRowNumber25.
- CommentAuthorzskoda
- CommentTimeJun 25th 2010
Thanks. You can write wiki way to have link working: http://www.math.harvard.edu/~lurie/papers/moduli.pdf.
-
- CommentRowNumber26.
- CommentAuthorTobyBartels
- CommentTimeJun 26th 2010
Even quicker wiki hack: http://www.math.harvard.edu/~lurie/papers/moduli.pdf. (See the Source.)
-
- CommentRowNumber27.
- CommentAuthorzskoda
- CommentTimeJun 26th 2010
New to me :) On the other hand, usually one writes different name.
I hear something like wild foxes…around here.
-
- CommentRowNumber28.
- CommentAuthorKevin Lin
- CommentTimeJun 26th 2010
- (edited Jun 26th 2010)
I added a few words about deformation theory via differential graded Lie algebras to the deformation theory page.
-
- CommentRowNumber29.
- CommentAuthorKevin Lin
- CommentTimeJun 26th 2010
I just noticed that there are two different pages for deformation theory and Deformation Theory… is this intentional?
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeJun 26th 2010
the capitalized entries are about references. Deformation Theory is supposed to be about the article by Lurie, deformation theory about the concept.
-
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeJun 26th 2010
FYI, Lurie has a new paper on deformation theory: http://www.math.harvard.edu/~lurie/papers/moduli.pdf
Thanks for mentioning this! I added links to it also to dg-Lie algebra and Jacob Lurie
-
- CommentRowNumber32.
- CommentAuthorjim_stasheff
- CommentTimeMar 5th 2011
NSF/CBMS Conference
on
Deformation Theory of Algebras and Modules
May 16-20, 2011
North Carolina State University -
- CommentRowNumber33.
- CommentAuthorjim_stasheff
- CommentTimeMar 5th 2011
http://www4.ncsu.edu/~lada/CBMS/cbms.htm -
- CommentRowNumber34.
- CommentAuthorzskoda
- CommentTimeMar 5th 2011
To make it a link: http://www4.ncsu.edu/~lada/CBMS/cbms.htm.
-
- CommentRowNumber35.
- CommentAuthorjim_stasheff
- CommentTimeMar 6th 2011
Thanks -
- CommentRowNumber36.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 6th 2011
- (edited Mar 6th 2011)
in the first part of my Utrecht notes (here) there’s a sketchy interpretation of the classical Kodaira-Spencer description of infinitesimal deformations of a smooth complex manifold as , where both and are seen as simplicial presheaves over some site of local models for complex manifolds (e.g., polydisks). in the abve formula is the tangebt sheaf seen as a functor on this (hypotetical?) site: it maps an object to the Lie algebra of holomorphic vector fields on .
I was wondering if the abstract machinery of deformations and cotangent complex isn’t just the natural abstract version of this, with the cotangent complex functor the right abstract substitute for (up to some duality)
-
- CommentRowNumber37.
- CommentAuthorzskoda
- CommentTimeMar 6th 2011
Did you compare your view with Toen-Vezzosi ? I mean the most elaborated example of their derived geometry is the cotangent complex interpreted as a tangent space to a derived moduli space. They were writing very extensively about these things (and that was the first thing which I remembered about derived geometry when coming to a conference at Nice in 2003 as a total outsider).
-
- CommentRowNumber38.
- CommentAuthorTim_Porter
- CommentTimeMar 7th 2011
I remember that (as I was there in Nice 2003 if you are talking of the CATS 2 conference). I’m afraid that I did not understand that much except that as I had seen Toen’s papers and Simpson’s as well I had some vague idea of what he was trying to do.
-
- CommentRowNumber39.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 7th 2011
thanks. I had a vague idea it had to be related, but the first time I tried to look at Toen-Vezzosi I had been unable to make contact with the classical picture so I gave it up. now I’ll try again.
-
- CommentRowNumber40.
- CommentAuthorTim_Porter
- CommentTimeMar 7th 2011
Through the 1990s, I had been looking at Quillen’s cohomology of commutative algebra stuff (motivated by deformation theory) and then at Illusie’s thesis, which took it further into Alg. Geom. From that direction the cotangent complex was more clearly linked into the classical def. theory. It struck me as important that Quillen MC ideas were (amongst other sources) an attempt to develop a deformation theory. (Things have come around full circle it seems.)
-
- CommentRowNumber41.
- CommentAuthorjim_stasheff
- CommentTimeMar 7th 2011
Tim,
Could you elaborate on that? I had learned of the cotangent complex from Mike Schlessinger directly in the context of deformation theory (in rational homotopy theory). -
- CommentRowNumber42.
- CommentAuthorTim_Porter
- CommentTimeMar 7th 2011
Just a word, Lichtenbaum and Schlessinger used a cotangent complex (actually a crossed module of commutative algebras) in deformation theory. Quillen’s introduction of what is called André-Quillen cohomology was in part following on from his earlier work on (?) PDEs and deformation theory. I would have to search back for that. Illusie’s thesis published as Springer lecture notes then used it in Alg. Geometry but I was not able to work out all the linkages in deformation theory of the classical form 9and have forgotten much that I did understand.:-()
Must rush.
-
- CommentRowNumber43.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2011
- (edited Mar 19th 2011)
Does anyone have any insights into Ralph Kaufmann’s use of (a slight generalisation of ) Turaev’s crossed -algebras and their link with Minor algebras of singularities with symmetries? It seems that this leads straight into equivaraint versal deformations etc. but I quickly get out of my comfort zone! The papers that I am looking at seem mostly to be from 8 years ago so perhaps the ideas have been pushed further forward. (My thought (probably half baked!) is that there should here be some (simple?, direct?) link with HQFts, equivariant TFTs, etc, and it would be good if that was made clear (if it exists).
-
- CommentRowNumber44.
- CommentAuthorjim_stasheff
- CommentTimeMar 19th 2011
@Tim:Lichtenbaum and Schlessinger used a cotangent complex (actually a crossed module of commutative algebras) in deformation theory.
Do you have a reference for that crossed alg interpretation?
for Minor algs? or was thaat supposed to me Milnor?
and which Kaufmann paper? -
- CommentRowNumber45.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2011
- (edited Mar 19th 2011)
Try Me: Homology of commutative algebras and an invariant of Simis and Vasconcelos, Jour. Alg., 99 (1986) pp. 458-465.
If you have a commutative algebra A and a set of elements X, (think of this as a presentation of the A-algebra ). Now form the free crossed module (of commutative algebras) on this, so you take the positively graded part of the polynomial algebra, A[X], and divide out by all elements of the form [x]{y] - x[y] (where I put [] around an element of it is considered in X and not if considered as an element of A. Of course, in the quotient (which is a commutative A-algebra but usually without unit (as it is a kernel)) x[y]= y[x] which is the way that Lichtenbaum and Schlessinger defined their cotangent complex, but they did not think of that as a multiplication. It is neat to interpret this (i) as the free crossed module on and (ii) as a quotient of the Koszul complex. This was done in that paper. I wanted to push that further but somehow did not manage to see clearly where it led.
It was Milnor, just my heavy fingers! The paper was ORBIFOLDING FROBENIUS ALGEBRAS in the Arxiv at http://arxiv.org/abs/math/0107163
-
- CommentRowNumber46.
- CommentAuthorTim_Porter
- CommentTimeMar 20th 2011
I should mention that the passage from a simplicial resolution (of a group or an algebra) to the relative abelianisation that I outline in the Menagerie (Ch 3) was ‘inspired’ by two separate things (i) Ronnie and Phil Higgins passage from crossed complexes to chain complexes, and (ii) Quillen’s introduction of the derived functor version of the cotangent complex.
-
- CommentRowNumber47.
- CommentAuthorjim_stasheff
- CommentTimeMar 20th 2011
I don't recall that terminology in Quillen's version of Andre-Quillen
Have you just updated the language
or another Quillen paper? -
- CommentRowNumber48.
- CommentAuthorTim_Porter
- CommentTimeMar 21st 2011
- (edited Mar 21st 2011)
He does not use ”elative abelianisation’. You’re right that is ’Tim-ese’. He does consider for a comm. alg. A, looks at the abelian group objects therein and his cotangent complex for a map , is the derived abelianisation functor from to followed by an identification of that as being , (plus, of course, the passage from simplicial objects to chain complexes, using Dold-Kan). I think I remember the process correctly.) I think of this process as abeliansiation relative to the object over which we are working. It may be more a ‘free abelian group object’ functor.
By Jon Beck’s results this is a very general situation. The link between the Kahler differentials and that ’relative’ form of abelianisation is quite general. In the corresponding case for it gives the Fox derivatives, etc. and the derived module of a presentation of a group. (That is explored further in a categorical setting in the paper I wrote with Rick Blute, Robin Cockett and Rob Seeley, but we have not handled the non-commutative case.) I was surprised to find that Quillen did not refer to the Fox derivatives case and its links with the classical bar resolution of a group, when he was discussing the construction.
-
- CommentRowNumber49.
- CommentAuthorUrs
- CommentTimeNov 28th 2011
at deformation theory I have tried to start organizing the long list of references into subsections, such as to make it more usable. But there is still lots of room for improvement.
-
- CommentRowNumber50.
- CommentAuthorzskoda
- CommentTimeNov 28th 2011
- (edited Nov 28th 2011)
Urs, I find your current division of references into subsections almost completely arbitrary. I do not know in which sense are Kontsevich topics lectures less introductory then the (I think harder) reference of Grothendieck, or by what sense is the paper of Efiomovb et al. a monograph. I have put most of the references there with great effort and the order had some sense to me before (I was putting usually simialr approaches one next to another). I am sorry, I appreciate your will to improve the bibliography (including new refernce by Doran, which is very new to me), but this time, I would strongly like to rollback instead of keeping this artificial division (the reference sbelong to so different approaches that it is better to leave for the reader to choose what is introductory for them).
-
- CommentRowNumber51.
- CommentAuthorUrs
- CommentTimeNov 28th 2011
Hi Zoran,
if there was some order before, it was compltely intransparent. If you have a way of ordering these, please do with some subsection headlines.
-
- CommentRowNumber52.
- CommentAuthorzskoda
- CommentTimeNov 28th 2011
- (edited Nov 28th 2011)
So what would be the sections headlines: approach via A-infinity algebras and operad, approach via direct methods, I think it is too vague to make such and I think it is not a good idea. It would just make a section longer and with added vague and long external qualifications. Works speak for themselves. I put a lot of effort to collect nice long list with links of carefulkly chosen references in very different approaches. You could have seen that the similar authors are one to another and it is not possible to quantify this into exact terms, and trying would result in disaster. At least all of it was in compact form and easy to print. The monograph etc. sections do not correspond to the reality so I woudl abandon it. A reader should choose from the literature those references and authors which from the tietles and aithors look familiar to her/him. Those which one does not see an apparent order are probably less known to her so she can simply skip it. Fragmenting a unique list in nonprecise way makes me wish not to compile next such list. I have contributed huge amount of references to nLab often with multiple links to arXiv, mathscinet etc. and I have really no wish to write more of something what will later get wrong qualifications. This is killing my enthusiasm.
-
- CommentRowNumber53.
- CommentAuthorzskoda
- CommentTimeNov 28th 2011
- (edited Nov 28th 2011)
Of course, in those lists when it makes sense I happily introduce the sections, but here I do not see a natural way to do it. One should not force it then.
-
- CommentRowNumber54.
- CommentAuthorUrs
- CommentTimeNov 28th 2011
This is killing my enthusiasm.
Just revert then. But it didn’t appear to me to be a useful list before. Sorry if that information kills your enthusiasm.
-
- CommentRowNumber55.
- CommentAuthorzskoda
- CommentTimeNov 28th 2011
- (edited Nov 28th 2011)
I am sorry, but I did not get any information how it becomes more useful by adding incorrect or approximate information, like that Efimov’s paper is a monograph and separating two references from the same author into different sections (in most of the cases it is anyway seen from the format of the entry if it is a monograph or a paper, so it is low relevant info) ? I suppose you likely did not read the page with intention to find a new good reference but with attention to change the page. My list was compiled with attention to list all main references in a plethora of different approaches and fields, from complex geometry to algebraic geometry, algebra, physics and topology…I understand and apologize this is not in line with strictly nPOV, but I am not a category theorist anyway.
-
- CommentRowNumber56.
- CommentAuthorUrs
- CommentTimeNov 28th 2011
incorrect
Can you fix it?
-
- CommentRowNumber57.
- CommentAuthorzskoda
- CommentTimeNov 28th 2011
- (edited Nov 28th 2011)
I can fix it in a way which is orthogonal to the organization which I thought of when spending an effort to create it. I am not sure that the way I would be fixing you would be useful for you if the original list was not. I want the final result to be good and am ready to wait for a ripe moment, rather than to spoil my own work with something I still do not feel ripe in ideas. There is no need to force.
-
- CommentRowNumber58.
- CommentAuthorTim_Porter
- CommentTimeNov 29th 2011
Can I just add that I find the list at present is a bit too long and it is difficult to find things in it. The minor idea of creating an alphabetical list might help. Perhaps a separate entry on references with ’advice’ for readers who are primarily interested in a particular (but fairly general) subtopic might be a way forward. That way a reference might be mentioned in several of the subheadings.
-
- CommentRowNumber59.
- CommentAuthorzskoda
- CommentTimeNov 29th 2011
- (edited Nov 29th 2011)
Alphabetical assumes one knows the author and one can not group the titles with similar approach. I find every one of the references there basic for some direction or style or one of the fundamental results. Most of them are about the whole subject and not about a subtopic. It is just different style of doing things. Some people start from homotopy abstractions and then concretise. Some start from complex analysis and then abstract. Some start with complex geometry and then abstract. Some start with algebraic manipulations like physicists. Some include also some global results while most are only about formal/infinitesimal deformation theory. There is no clear subdivision, and it actually inhibits natural associating. Adding additional subtitles and non-content terms (like “monographs”, while it is clear from a format weather ist is in a journal or not) just makes list longer without added content. For example first several references are always simpler and more intyrdouctory, though not exactly introductions, then you have a group of 5-6 references of modern authors like Illusie, Kontsevich, Lurie, Efimov/Orlov/Lunts, then after that mainly algebraic goemetry and historical references from early days (or modern presentations of similar point of view). But there is no clear subdivision and trying it would be artificial (I am thinking of one in future when the entry gets more complete but it is not ready for that).
-
- CommentRowNumber60.
- CommentAuthorUrs
- CommentTimeNov 29th 2011
- (edited Nov 29th 2011)
Hey Zoran,
you can stop ranting about how you dislike the section headers that I added. I did get it already the first time.
But as Tim confirms now, the fact remains that the list as was and as is is not useful. It looks like a huge random list of reference with no structure. If you had a structure in mind when creating it, this has not become visible.
So in the interest of the usefulness of the entry, it would be good to add some information on how somebody looking for information might go about it, which references would be for which purpose.
It would be great if you could use the energy and time you have to express strong opinions here to add comments to that reference list, if you care about it being useful.
-
- CommentRowNumber61.
- CommentAuthorzskoda
- CommentTimeNov 29th 2011
- (edited Nov 29th 2011)
Why would I spend the time NOW ?? Just because you NOW want it your way ? I had a plan for future, when I will work on that, maybe in a year or year and half, what is small time on the nLab period; for the structure I envision this entry needs much MORE references. I very often change my activity to fit your current interests (what you rarely notice) but can not do that every time you get attention to something. I think you want the lab to be for fast navigation through the pointers which are very familiar to you. These references are not your choice so you do not find them that useful. If you really needed to study and wanted to study you would open those and find it useful as they are very good references, carefully chosen and have links etc. But it was not your wish to understand those references it seems but to have a look form far away to navigate quickly. I like to print a useful page before a seminar or a discussion with a student. I want to print dense information and not empty nLab structure pointers, I do not want to scroll and staple 10 pages but have it in compact form. When I study page which I do not understand like many of yours I still don’t (this is not a critique!) I study it for hours and do not expect to have pointers made MY way in the text. You made them with your expertise and I trust you and read it slowly. I do not expect to find my way through unknown material in seconds.
I do not have energy and time to work this semester on deformation theory. The list is useful, I myself used it many times, you can add more references which are closer to you.
it would be good to add some information on how somebody looking for information might go about it
It makes list longer and harder to view, print and picture. Most files have known mathematician names, TITLES (which are seen as specialized or not) and LINKS which can be opened in seconds. Interested reader either knows the references and will just use nLab as a pointer to links and to exact place to find it, or is new to this and will slowly get acquired to names and titles which look interesting. You have no problem navigatiing through hundreds of references in any paper you ever opened in front of my eyes, but it si a problem within 20 mainly known refernces on the list I compiled. I can not understand this.
I did get it already the first time.
59 is not addressed to you.
to add comments to that reference list, if you care about it being useful
I did spend the time to erase the useless copying of abstract of the Markl’s paper to the entry: the link to the abstract is in the citation and takes 1 second to click and see it. This makes it cleaner.
If you had a structure in mind when creating it, this has not become visible.
I can say the lack of structure for many pages in the Lab: it is work in progress and some time it will be improved.
-
- CommentRowNumber62.
- CommentAuthorUrs
- CommentTimeNov 29th 2011
Why would I spend the time NOW ??
Because you are spending time on writing all these long comments here. I was thinking this time could be spent more productively. But never mind.
-
- CommentRowNumber63.
- CommentAuthorzskoda
- CommentTimeNov 29th 2011
- (edited Nov 29th 2011)
Urs, I know you repeat that phrase, but creative work on more complicated nLab issues requires much more concentration and time than a quick chat, by orders of magnitude. I would need half a day only to concentrate on this area which I am not working this year on, refreshing memories and alike. And moreover if one conentrates on something attractive then one can not receontrate back on burning issues one has in other parts of the life. I would better not mention in which situation I am now, and better not open working any topic which is attractive to me.
-
- CommentRowNumber64.
- CommentAuthorzskoda
- CommentTimeNov 30th 2011
- (edited Nov 30th 2011)
It occurs to me: the best starting reference should be Lab’s text itself and in future we may expect that the text of the entries will cite the more specialized references listed at the bottom. So eventually one won’t scroll the reference list that much but rather come naturally to those from the pointers in the text. Then one can be more specific than it is tasteful for overall comment/characterization of a reference. I can however say, I am personally lousy (read: still almost never do) in linking actual Lab text to the references on the bottom (partly as Itend to forget the format for doing this, not being LaTeX and am laisy to look it up).
-
- CommentRowNumber65.
- CommentAuthorjim_stasheff
- CommentTimeNov 9th 2012
Slight change in focus: the albatross has landed, i.e.
Deformation theory and rational homotopy type is now on the arXiv.
That;s the ?long awaited?? paper by me and Mike Schlessinger. -
- CommentRowNumber66.
- CommentAuthorjim_stasheff
- CommentTimeNov 10th 2012
For those of you who are happy with the fancier theoretical settings now available, the examples of actual calculations might still be of interest.
Comments are most welcome. -
- CommentRowNumber67.
- CommentAuthorRodMcGuire
- CommentTimeNov 11th 2012
-
- CommentRowNumber68.
- CommentAuthoradeelkh
- CommentTimeJul 7th 2014
I added the reference
- Dennis Gaitsgory, Lie theory from the point of view of derived algebraic geometry, Lecture notes from a mini-course, Nantes, 2014, web.
-
- CommentRowNumber69.
- CommentAuthorGuest
- CommentTimeFeb 2nd 2019
The link given by David to the Historical Annotated Bibliography is now broken.Thanks! -
- CommentRowNumber70.
- CommentAuthorDavid_Corfield
- CommentTimeFeb 3rd 2019
So this regards my addition in #16 to the main page deformation theory. I think
C. Doran, Deformation Theory: An Historical Annotated Bibliography
became
C. F. Doran, S. Wong, “Deformation Theory: An Historical Annotated Bibliography,” Chapter 2 in book : Deformation of Galois Representations, to appear in the AMS-IP Studies in Advanced Mathematics Series
I’ll change that. I don’t see it’s available online now.
-
- CommentRowNumber71.
- CommentAuthorGuest
- CommentTimeFeb 3rd 2019
Thanks again! I also got the impression that it's no longer available online: what a pity.
1 to 71 of 71