nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 5th 2010
in order to discuss weighted limits in my revision of limits, I introduced a stubby notion of weighted join of quasi-categories. The construction and the subsequent notion of weighted limit seem quite natural, but everithing now seems too simple, so I fear to have completely misunderstood the notion of weighted limit.. :(
could anybody give a look? -
- CommentRowNumber2.
- CommentAuthorMike Shulman
- CommentTimeJan 5th 2010
Regarding limits, can I suggest that the nlab page on limits should not start out talking about quasicategories? (-: I'm not clear exactly what your plan is, but the page you have called limits (domenicofiorenza) doesn't seem appropriate for an nlab page called "limit" instead of, say, "limit in a quasicategory". Perhaps I have misunderstood what you're doing.
-
- CommentRowNumber3.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 6th 2010
you did not misunderstood: there has been some speculation between urs and me in the thread "objects and tools to compute them" on the oppurtunity of organizing nLab entries according to the pattern idea and motivation/infinity-categorical definition/unwrapping of the definition and specialization to categories/examples/how to compute.
since abstract speculation on issues like this leads nowhere we agreed to give a try and rewrite a classic such as limit, to see how it came out. not to affect such a fundamental entry as limit the revision attemp is developed in my private area. as it will be completed it will be possible to discuss what to do with it: use it to replace "limit" in the nLab? merge it into "limit in a quasicategory" in the nLab? leave it as a memento of how an nLab page should *not* look? :-)
I've no preferences, my attitude in developing limit is to consider it an exercise in style. but maybe something good can come out of it anyway. for instance, the approach to weighted limits via weighted joins, if I did not completely misunderstood the definition of weighted limit, may happen not to be so bad. -
- CommentRowNumber4.
- CommentAuthorMike Shulman
- CommentTimeJan 6th 2010
I made a couple comments.
-
- CommentRowNumber5.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 6th 2010
Thanks. I see calling the category was a really bad choice. Now I've edited the page. -
- CommentRowNumber6.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 7th 2010
@Mike: cograph of a profunctor, as you suggested, seems to perfecty do what I had in mind, thanks! I also added a short comment to try to explain what I meant by changing the notation. -
- CommentRowNumber7.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 8th 2010
Mike, I'm glad in the end we managed to understand each other :-)
As I'll be able to find time for, I'll rewrite everithing in weighted join in terms of cographs as you suggest.
Just a final question: is not what I call a weighted initial object for D the weighted limit of id:D-->D? what am I missing? -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeJan 8th 2010
i don't have the energy to look into this right now, but am interested. If Mike finds a second I am sure you two will find a good notion of weighted (oo,1)-limit.
-
- CommentRowNumber9.
- CommentAuthorMike Shulman
- CommentTimeJan 8th 2010
- (edited Jan 8th 2010)
A W-weighted limit of
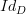 would be an object Z such that
would be an object Z such that ) hom_D(Y,Z) \cong [D,Set](W,hom_D(Y,-))](/extensions/vLaTeX/cache/latex_a944ccd260dee09568d5338561d164e3.png) for all Y. In particular, looking at
for all Y. In particular, looking at 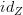 on the left-hand side would give you a canonical set of
on the left-hand side would give you a canonical set of 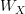 maps from Z to X for all X, i.e. a map
maps from Z to X for all X, i.e. a map 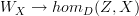 , but I don't see any reason for that map to be a bijection.
, but I don't see any reason for that map to be a bijection. -
- CommentRowNumber10.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 8th 2010
- (edited Jan 8th 2010)
I see, and neither I can see a reason for to be a bijection at the moment. what confuses me is that for the constant weight , this is actually a bijection, and a limit of turns out to be an initial object for . yet, the construction above, specialized to , apparently only provides a canonical map , thus only seems only to say that for every there is a certain distinguished map . but looking at things more in detail one finds that is the unique map from to . I'll have to think more on this. -
- CommentRowNumber11.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 13th 2010
- (edited Jan 13th 2010)
Mike, I've finally found some time to think again to the definition of weighted limit, and now I totally agree with your objection, thanks.
Summing up, things should go as follows. Let be a functor and let be a weight. If denotes the terminal category, then and can be seen as a profunctor from to . The cograph of this profunctor is the "weighted join" . The weighted limit of is, if it exists, a terminal object in the category of functors extending . If a weighted limit in this sense exists, then the object of has the universal property of the weighted limit of the "object with universal property" definition of weighted limit. And vice versa, given an object with the universal property, one can canonically extend to by setting . Hence the two notions are equivalent, and one can use the "terminal functor" definition to generalize the notion of weighted limit to quasicategories. What do you think? -
- CommentRowNumber12.
- CommentAuthorMike Shulman
- CommentTimeJan 14th 2010
Yes, that seems right to me.
1 to 12 of 12