nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: G-equivariant stable homotopy theory
Bottom of Page1 to 33 of 33
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 19th 2010
- (edited Jan 19th 2010)
Here is a vague question, (with an eye towards Mike):
I am visiting John Greenlees et al in Sheffield. Greenlees is thinking about G-equivariant stable homotopy theory with Peter May, a good survey being
Equivariant stable homotopy theory.
He says they'd like a "May recognition theorem" for this case but don't have one, i.e. one would like to be able to say
grouplike G-equivariant spaces with a "G-equivariant
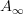 -action" are equivalent to connective G-equivariant spectra.
-action" are equivalent to connective G-equivariant spectra.Now, I am thinking: what (oo,1)-topos is G-equivariant spectra the stabilization of? Should that be oo-prestacks on
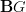 (the one-object groupoid)?
(the one-object groupoid)?If so, this connects with a general thing that I have started thinking about while ago: to have a "May recognition theorem" in a general oo-stack oo-topos we'd need to internalize the notion of
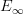 -operad into that. I think the right notion should be modeled by a dendroidal presheaf on the given site: a "parameterized" oo-operad.
-operad into that. I think the right notion should be modeled by a dendroidal presheaf on the given site: a "parameterized" oo-operad.With some people I have been thinking about this for the case that the site is one that models synthetic differential geometry. We wanted to see a smooth action of
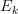 on smooth k-fold loop spaces.
on smooth k-fold loop spaces.But G-equivariant stable homotopy theory might be another application, with the site being
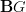 .
.Does anyone see what I mean? :-)
Any thoughts?
-
- CommentRowNumber2.
- CommentAuthorMike Shulman
- CommentTimeJan 19th 2010
Coincidentally enough, just today here at Chicago, Anna Marie Bohmann gave a proseminar talk about "basic notions of equivariant stable homotopy theory."
Equivariant homotopy theory is full of traps for the categorically minded. The first trap is that when algebraic topologists talk about G-equivariant spaces, they aren't talking about
 -groupoids with a G-action (=
-groupoids with a G-action (=  -prestacks on
-prestacks on 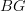 ). It's true that the usual model category used to model G-equivariant spaces is the category of topological spaces with a G-action, but the weak equivalences used are not the "objectwise" ones (that's what would model
). It's true that the usual model category used to model G-equivariant spaces is the category of topological spaces with a G-action, but the weak equivalences used are not the "objectwise" ones (that's what would model  -groupoids with a G-action). Instead the weak equivalences are the G-maps that induce weak equivalences on the space of H-fixed-points for every (closed) subgroup H of G.
-groupoids with a G-action). Instead the weak equivalences are the G-maps that induce weak equivalences on the space of H-fixed-points for every (closed) subgroup H of G.In fact, another model category that models the same
 -category of "G-equivariant spaces" is the category of diagrams on the orbit category
-category of "G-equivariant spaces" is the category of diagrams on the orbit category 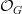 of G, where now the weak equivalences are "objectwise". That is, a diagram X consists of a space X(H) for each subgroup H of G (thought of as the "H-fixed points"), and a map from X to Y is a weak equivalence if each map from X(H) to Y(H) is a weak equivalence. (This equivalence is called Elmendorf's Theorem.) So I think a more correct higher-categorical point of view on the algebraic topologists' "G-equivariant spaces" is that they are diagrams of
of G, where now the weak equivalences are "objectwise". That is, a diagram X consists of a space X(H) for each subgroup H of G (thought of as the "H-fixed points"), and a map from X to Y is a weak equivalence if each map from X(H) to Y(H) is a weak equivalence. (This equivalence is called Elmendorf's Theorem.) So I think a more correct higher-categorical point of view on the algebraic topologists' "G-equivariant spaces" is that they are diagrams of  -groupoids on
-groupoids on 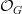 .
.The second trap lies in what you mean by "spectrum" and "stabilization." This came up on MathOverflow a bit ago, although I can't find it right now. On the one hand there is the "obvious" notion of a "G-spectrum," in which you have a sequence of G-spaces
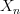 with maps
with maps 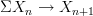 and so on. I think this should be what you get if you stabilize the
and so on. I think this should be what you get if you stabilize the  -category of G-spaces. Equivariant algebraic topologists call these "naive" G-spectra, but this isn't the sort of spectrum they are most interested in.
-category of G-spaces. Equivariant algebraic topologists call these "naive" G-spectra, but this isn't the sort of spectrum they are most interested in.What they care more about are "genuine" G-spectra, which come with spaces
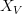 for all finite-dimensional representations V of G. (More precisely, naive and genuine G-spectra exist at opposite ends of a continuum; the general notion of spectrum is indexed on all V contained in some fixed infinite-dimensional representation U, called a "universe".) These genuine G-spectra correspond to generalized Bredon cohomology theories in the same way that ordinary spectra corresponding to the usual generalized cohomology theories. However, it's not at all clear to me that they are the "stabilization" of anything in the sense used by
for all finite-dimensional representations V of G. (More precisely, naive and genuine G-spectra exist at opposite ends of a continuum; the general notion of spectrum is indexed on all V contained in some fixed infinite-dimensional representation U, called a "universe".) These genuine G-spectra correspond to generalized Bredon cohomology theories in the same way that ordinary spectra corresponding to the usual generalized cohomology theories. However, it's not at all clear to me that they are the "stabilization" of anything in the sense used by  -category-theorists.
-category-theorists.Now what about recognition principles? For the
 -categorical version of stabilization, I would not expect to need to "internalize" the notion of operad at all. Compare this to how we don't need to "internalize" the theory of rings when we talk about ringed 1-topoi—we just talk about internal models of the fixed external theory. Similarly, I would expect a notion of "grouplike
-categorical version of stabilization, I would not expect to need to "internalize" the notion of operad at all. Compare this to how we don't need to "internalize" the theory of rings when we talk about ringed 1-topoi—we just talk about internal models of the fixed external theory. Similarly, I would expect a notion of "grouplike 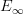 -object" to be the same in any
-object" to be the same in any  -topos and give a recognition principle relative to its
-topos and give a recognition principle relative to its  -categorical stabilization (but I don't know if anyone has done this).
-categorical stabilization (but I don't know if anyone has done this).For genuine G-spectra, the question is much trickier and does involve internalizing the notion of operad. Peter May says that he's known how to do it for 30 years, at least when G is a finite group, but never found the time to write it down. When I asked him about this, he offered to contribute to the discussion directly, so I'll let him explain it himself.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 19th 2010
- (edited Jan 19th 2010)
Thanks Mike, nice answers!
What they care more about are "genuine"
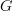 -spectra, which come with spaces
-spectra, which come with spaces 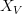 for all finite-dimensional representations
for all finite-dimensional representations 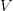 of
of 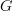 .
.Yes, this I learned meanwhile. This is the G-equivariant generalization of coordinate-free spectrum.
Instead the weak equivalences are the G-maps that induce weak equivalences on the space of H-fixed-points for every (closed) subgroup H of G.
Ah, thanks for amplifying this. Hm, but could this be a further localization of the model structure of oo-stacks on BG?
So I think a more correct higher-categorical point of view on the algebraic topologists' "G-equivariant spaces" is that they are diagrams of
 -groupoids on
-groupoids on 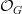 .
.Aha, interesting. But concerning the terminology: what kind of diagrams is this about?
I would expect a notion of "grouplike
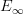 -object" to be the same in any
-object" to be the same in any  -topos and give a recognition principle relative to its
-topos and give a recognition principle relative to its  -categorical stabilization (but I don't know if anyone has done this).
-categorical stabilization (but I don't know if anyone has done this).Right, the main result of Ek-Algebras , summarized here says essentially this, for finite k. I was thinking that to get it exactly, one needs a bit more, but now I am not so sure anymore.
For genuine G-spectra, the question is much trickier and does involve internalizing the notion of operad. Peter May says that he's known how to do it for 30 years, at least when G is a finite group, but never found the time to write it down. When I asked him about this, he offered to contribute to the discussion directly, so I'll let him explain it himself.
I'd be very interested.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeJan 19th 2010
- (edited Jan 19th 2010)
I am still reading up on this stuff, but now i am wondering:
theorem 2.3, page 12 of the survey states that despite its definition in terms of H-fixed points, a weak equivalence of G-spectra is after all precisely one that is a weak equivalence over each index space.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeJan 20th 2010
now i am wondering:
Ah, never mind, I get it. Equivalence of G-spaces is defined again H-wise.
Okay, I'll summarize the basic defintions at equivariant stable homotopy theory
-
- CommentRowNumber6.
- CommentAuthorMike Shulman
- CommentTimeJan 20th 2010
but could this be a further localization of the model structure of oo-stacks on BG?
No, rather the reverse; this defines fewer weak equivalences than the "objectwise" ones.
what kind of diagrams is this about?
I don't know what you mean. What kind of diagrams are there?
-
- CommentRowNumber7.
- CommentAuthorDavidRoberts
- CommentTimeJan 20th 2010
A mix up in terminology, I think. 'Diagrams' referring to functors,
O_G --> oo-Gpd,
but perhaps Urs was wondering if these are 1-functors or weak functors? -
- CommentRowNumber8.
- CommentAuthorMike Shulman
- CommentTimeJan 20th 2010
I don't think it matters whether you mean strict 1-functors or weak
 -functors.
-functors. -
- CommentRowNumber9.
- CommentAuthorDavidRoberts
- CommentTimeJan 20th 2010
I suppose it's the difference between homotopy coherent diagrams and ordinary diagrams. -
- CommentRowNumber10.
- CommentAuthorMike Shulman
- CommentTimeJan 20th 2010
Yes, and all homotopy coherent diagrams of spaces can be rectified to strict ones.
-
- CommentRowNumber11.
- CommentAuthorDavidRoberts
- CommentTimeJan 20th 2010
ok - I thought I had read this somewhere, but it seemed counter-intuitive. -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeJan 20th 2010
Oh, I see, "diagram of oo-groupoids" as an equivalent way to say "presheaf of oo-groupoids" .
but it seemed counter-intuitive.
It's one of the central punchlines of Lurie's book, too: oo-stacks are modeled by simplicial presheaves. That in particular means that every "pseudo-oo-functor" to oo-groupoids is equivalent to one that does respect all composition on the nose. It's kind of a semi-strictification theorem.
No, rather the reverse; this defines fewer weak equivalences than the "objectwise" ones.
I am likely mixed up about this: the theorem is that the weak equivalences are objectwise the weak equivalences of G-spaces, which in turn are those that are ordinary weak equivalences on spaces of H-fixed points for all H. That seems to be a weaker condition than being a weak equivalence on the whole space over the given object.
So I think a more correct higher-categorical point of view on the algebraic topologists' "G-equivariant spaces" is that they are diagrams of \infty-groupoids on \mathcal{O}_G.
I'd really enjoy a fully correct statement along these lines. But not today, I have to concentrate on something else.
-
- CommentRowNumber13.
- CommentAuthorMike Shulman
- CommentTimeJan 20th 2010
but it seemed counter-intuitive.
It is a bit counter-intuitive, since definitely not all pseudo
 -functors are equivalent to strict ones. In general one needs the domain to be "cofibrant" in order to strictify. But the
-functors are equivalent to strict ones. In general one needs the domain to be "cofibrant" in order to strictify. But the  -category of spaces is special in that it's "fibrant" in some dual sense. A low-dimensional version of this fact is that every Grothendieck fibration is equivalent to a split one.
-category of spaces is special in that it's "fibrant" in some dual sense. A low-dimensional version of this fact is that every Grothendieck fibration is equivalent to a split one.the weak equivalences of G-spaces... are those that are ordinary weak equivalences on spaces of H-fixed points for all H. That seems to be a weaker condition than being a weak equivalence on the whole space
The whole space is the space of fixed points for the trivial subgroup of G. So if a map is a weak equivalence on spaces of H-fixed points for all H, it is in particular a weak equivalence on the whole space. But if you consider, for instance, the map from EG to 1, it is a weak equivalence on the whole space since EG is contractible, but it is not a weak equivalence on H-fixed points for any other H, since EG has a free G-action while 1 has a trivial G-action.
I'd really enjoy a fully correct statement along these lines.
Elmendorf's theorem isn't sufficiently correct for you? (-: Or did you just want me to state it more precisely?
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeJan 20th 2010
Elmendorf's theorem isn't sufficiently correct for you? (-:
Hey, wait, it was you who used the words: "more correct" for the statement that I think I am interested in. To me, "more correct" means also "not fully correct".
But, whatever, I have some other duties out of the way and now want to pin this issue down precisely, yes.
Had a chat today with some experts at Sheffield (won't mention the names until I am sure I am reproducing what they told me correctly), and when I mentioned this idea here to them they said : yes, sure, the category of equivariant spectra is a stabilization of that of simplicial presheaves on the orbit category. Well, then the other of the two experts said: "or is it simplicial presheaves on the stabilization of the orbit category, or is that the same? " and we had finished our beer and had to part before that had been clarified, but this sounds promising to me.
I was told that this is in some article by Schwede and Shipley.
Or did you just want me to state it more precisely?
I'd be grateful for whatever details I can get hold off. I'll start looking for and at literature right now. But whatever you have, I'd be very grateful if you share it.
This should make a good nLab entry.
-
- CommentRowNumber15.
- CommentAuthorMike Shulman
- CommentTimeJan 21st 2010
Ah. To me "more correct" does not imply "not fully correct."
the category of equivariant spectra is a stabilization of that of simplicial presheaves on the orbit category
I'd be pretty surprised if that were true for "genuine" G-spectra and this notion of stabilization. But hey, I've been surprised before. Scanning through Schwede and Shipley's papers on Mathscinet I can't find anything that looks like this.
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
To me "more correct" does not imply "not fully correct."
Admittedly, strictly logically speaking that's more correct than my implication. ;-) Do you think of "more correct" as being more polite than "correct"?
Scanning through Schwede and Shipley's papers on Mathscinet I can't find anything that looks like this.
I haven't found it either, yet. But then, it's 3am here in GB and my wireless connection is shaky...
I'd be pretty surprised if that were true for "genuine" G-spectra and this notion of stabilization.
Okay, but what's going on then?
G-Spaces are simplicial presheaves on
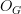 , so there is nothing more natural than passing to the univeral stabilization. In which sense would this be a worse concept than the "genuine G-spectra"s considered in the literature? What is it that makes the definition of "genuine G-spectra" good? From an abstract-nonsense point of view. the concept
, so there is nothing more natural than passing to the univeral stabilization. In which sense would this be a worse concept than the "genuine G-spectra"s considered in the literature? What is it that makes the definition of "genuine G-spectra" good? From an abstract-nonsense point of view. the concept 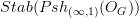 is a GoodConcept™. On what basis is this being rejected?
is a GoodConcept™. On what basis is this being rejected?You said there are many traps in G-equivariant theory for the category-theoretic minded. I can see that. So who set up these traps?!? ;-)
The first "trap" we saw was that
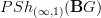 is not quite as interesting as
is not quite as interesting as 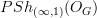 . Said this way, it is not so much a trap but just the observation that the group G encodes various different categories on which one can consider presheaves, and some of them may be more interesting than others. So I am not worried about this trap.
. Said this way, it is not so much a trap but just the observation that the group G encodes various different categories on which one can consider presheaves, and some of them may be more interesting than others. So I am not worried about this trap.But I don't understand yet what makes the non-standard by-hand notion of stabilization of G-spaces (the "genuine" one) better than the canonical abstract-nonsense definition. Can you help me see this?
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
by the way, I started equivariant homotopy theory with a quick statement of Elmendorf's theorem
-
- CommentRowNumber18.
- CommentAuthorHarry Gindi
- CommentTimeJan 21st 2010
"The name 'operad' is a word that I coined myself, spending a week thinking of nothing else." -
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
Hah, I think I found the intended reference:
Example 3.4 (i) in
Schwede, Schipley, Classification of stable model categories (pdf)
gives something like two thirds of what was mentioned in that conversation that I reported. it's the statement about functors on the stabilization of the orbit category.
'I'll call it quits now. See you tomorrow!
-
- CommentRowNumber20.
- CommentAuthorDavidRoberts
- CommentTimeJan 21st 2010
Burning the midnight oil indeed! -
- CommentRowNumber21.
- CommentAuthorzskoda
- CommentTimeJan 21st 2010
"diagram of oo-groupoids" as an equivalent way to say "presheaf of oo-groupoids"
wouldn't a diagram imply "covariant"
-
- CommentRowNumber22.
- CommentAuthorMike Shulman
- CommentTimeJan 21st 2010
@Zoran: all functors are covariant when you choose their domain correctly. (-:
Do you think of "more correct" as being more polite than "correct"?
Perhaps. I think I was just intending it as more "modest," i.e. not necessarily asserting that this is THE correct way to think about it, just that it's the best one I know.
Regarding the Schwede-Shipley result, it looks like what they're saying is that the G-equivariant stable category is equivalent to the category of presheaves of (ordinary) spectra on the stabilization of the orbit category. I can believe that, because the relevant "stabilization" of the orbit category is constructed using the original definition of the G-equivariant stable category and thus includes information about all representations. I'm not sure whether this would also be equivalent to the stabilization (now in the
 -categorical sense) of the category of (unstable) simplicial presheaves on the stabilized orbit category.
-categorical sense) of the category of (unstable) simplicial presheaves on the stabilized orbit category.I'm not the best person to explain why "genuine" equivariant spectra are better than "naive" ones. We talked a bit about it in proseminar yesterday, but I'm not sure I can reproduce it correctly. Maybe if Peter shows up, he can explain it. Possibly one reason had to do with being able to embed an equivariant manifold into a representation?
-
- CommentRowNumber23.
- CommentAuthorMike Shulman
- CommentTimeJan 21st 2010
I'm not sure whether this would also be equivalent to the stabilization (now in the
 -categorical sense) of the category of (unstable) simplicial presheaves on the stabilized orbit category.
-categorical sense) of the category of (unstable) simplicial presheaves on the stabilized orbit category.No, wait, that doesn't even make sense—the stabilized orbit category is a spectral category, not a simplicial category, so I don't even know how to define simplicial presheaves on it.
-
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeJan 22nd 2010
- (edited Jan 22nd 2010)
Right, yes. Now I have finally read the article carefully. Too bad that you beat me to correcting this. I wanted to correct me myself now! :-)
While their result 3.3.3 is about spectrum-enriched presheaves, not simplicially enriched presheaves, it occurred to me that this must be something like the model category analog of the "stable Giraud theorem".
What I mean is the material now at Stabilization and localization of presheaf (oo,1)-categories, summarizing two and a half statements in Lurie's StabCat.
Probably this stable Giraud theorem is something I should ponder a bit in the light of our discussion here.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeJan 22nd 2010
stub for stable model category
-
- CommentRowNumber26.
- CommentAuthorzskoda
- CommentTimeJan 22nd 2010
If we take the Baez-Dolan terminology where quasicategories are only one of the models for (infinity,1)-categories then it is not true what is said in the entry on stable infinity categories that the notion has been "clear to some experts" but first written and sistematized by Lurie.
Namely, in Segal model for (infinity,1)-categories, the stable Segal categories were beforehand extensively studied in published literature by Toen et al.
-
- CommentRowNumber27.
- CommentAuthorMike Shulman
- CommentTimeJan 24th 2010
<p>Here's Peter May's contribution, starting with a quote from me:</p> <blockquote> <p>For genuine G-spectra, the question is much trickier and does involve internalizing the notion of operad. Peter May says that he's known how to do it for 30 years, at least when G is a finite group, but never found the time to write it down. When I asked him about this, he offered to contribute to the discussion directly, so I'll let him explain it himself.</p> </blockquote> <p>Ok, here goes. The quote from Mike is entirely accurate, except that I have no idea what is meant by internalizing the notion of operad: as I defined operads in the first place, back in 1971, they need no modification. [Ed: I was just referring to the fact that the operads live in the category of G-spaces. -Mike] Last year I wrote a modernized (but not bowdlerized: no <img src="/extensions/vLaTeX/cache/latex_5b4e8bf1a57dcb0e372c2512e8f20c01.png" title="(\infty,1)" style="vertical-align:-20%;" class="tex" alt="(\infty,1)" />-categories, which make no serious contribution to the mathematics at hand) outline of the May recognition principle in</p> <p>``What precisely are <img src="/extensions/vLaTeX/cache/latex_6231d550b2577147b964d6e2dd2521cb.png" title="E_{\infty}" style="vertical-align:-20%;" class="tex" alt="E_{\infty}" /> ring spaces and <img src="/extensions/vLaTeX/cache/latex_6231d550b2577147b964d6e2dd2521cb.png" title="E_{\infty}" style="vertical-align:-20%;" class="tex" alt="E_{\infty}" /> ring spectra?''</p> <p>Geometry <img src="/extensions/vLaTeX/cache/latex_402fd545e9720027cf1d2f5bece29243.png" title="\&" style="vertical-align:-20%;" class="tex" alt="\&" /> Topology Monographs 16(2009), 215--282.</p> <p>Those wanting more details in the nonequivariant situation are referred there. For a finite group <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />, the outline works in exactly the same way, but the argument fails at the main step when <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" /> is a compact Lie group. In fact it already fails when <img src="/extensions/vLaTeX/cache/latex_90390df960ef5e2169ba660042eb7e4f.png" title="G = S^1" style="vertical-align:-20%;" class="tex" alt="G = S^1" />.</p> <p>The idea is a variant of the Beck monadicity theorem. Let <img src="/extensions/vLaTeX/cache/latex_011bd7c5d63bbc66aa8b463533d65d2a.png" title="\Sigma^{\infty}" style="vertical-align:-20%;" class="tex" alt="\Sigma^{\infty}" /> be the suspension <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spectrum functor from <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spaces to (genuine) <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spectra and let <img src="/extensions/vLaTeX/cache/latex_54dcd8d3252192299107e71e8c44583e.png" title="\Omega^{\infty}" style="vertical-align:-20%;" class="tex" alt="\Omega^{\infty}" /> be its right adjoint, which takes a <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spectrum to its <img src="/extensions/vLaTeX/cache/latex_ae346e845f99fb153f8286e4b3872efe.png" title="0" style="vertical-align:-20%;" class="tex" alt="0" />-th space. The main point is to approximate the monad <img src="/extensions/vLaTeX/cache/latex_d7d0e9019741b1d9d97d24fa9c317298.png" title="\Omega^{\infty} \Sigma^{\infty}" style="vertical-align:-20%;" class="tex" alt="\Omega^{\infty} \Sigma^{\infty}" /> on the category of <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spaces by the monad <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> associated to an <img src="/extensions/vLaTeX/cache/latex_6231d550b2577147b964d6e2dd2521cb.png" title="E_{\infty}" style="vertical-align:-20%;" class="tex" alt="E_{\infty}" /> <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-operad <img src="/extensions/vLaTeX/cache/latex_6ad8e42c94ee85417e3a147612767b08.png" title="\mathcal{C}" style="vertical-align:-20%;" class="tex" alt="\mathcal{C}" />.</p> <p>So what is an <img src="/extensions/vLaTeX/cache/latex_6231d550b2577147b964d6e2dd2521cb.png" title="E_{\infty}" style="vertical-align:-20%;" class="tex" alt="E_{\infty}" /> <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-operad? Well, a <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-operad is just an operad in the cartesian monoidal category of <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spaces. Its <img src="/extensions/vLaTeX/cache/latex_bdfbe95513604bb75d9d6071a5f9ddbe.png" title="j" style="vertical-align:-20%;" class="tex" alt="j" />-th space is a <img src="/extensions/vLaTeX/cache/latex_c91354313d5d24230fde079548911f3d.png" title="G\times \Sigma_j" style="vertical-align:-20%;" class="tex" alt="G\times \Sigma_j" />-space, where <img src="/extensions/vLaTeX/cache/latex_9ebf6f16d279e921480ef527f80905f9.png" title="\Sigma_j" style="vertical-align:-20%;" class="tex" alt="\Sigma_j" /> is the <img src="/extensions/vLaTeX/cache/latex_bdfbe95513604bb75d9d6071a5f9ddbe.png" title="j" style="vertical-align:-20%;" class="tex" alt="j" />-th symmetric group, and it must be the total space of a universal <img src="/extensions/vLaTeX/cache/latex_dd9610fbf9d460b65d9b98e28e50b28c.png" title="(G,\Sigma_j)" style="vertical-align:-20%;" class="tex" alt="(G,\Sigma_j)" />-bundle. When <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" /> is trivial, this says that it is a contractible space with a free <img src="/extensions/vLaTeX/cache/latex_9ebf6f16d279e921480ef527f80905f9.png" title="\Sigma_j" style="vertical-align:-20%;" class="tex" alt="\Sigma_j" />-action. One can start with any such operad <img src="/extensions/vLaTeX/cache/latex_1a9cfd2dbb38672c77272735266aa8b7.png" title="\mathcal{D}" style="vertical-align:-20%;" class="tex" alt="\mathcal{D}" />, but there is a certain such operad, <img src="/extensions/vLaTeX/cache/latex_40f53e676902ae7872b9f7478da1169d.png" title="\mathcal K" style="vertical-align:-20%;" class="tex" alt="\mathcal K" /> say, that acts naturally on infinite loop <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spaces, which are the <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spaces that are <img src="/extensions/vLaTeX/cache/latex_ae346e845f99fb153f8286e4b3872efe.png" title="0" style="vertical-align:-20%;" class="tex" alt="0" />-th spaces of <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spectra. Set <img src="/extensions/vLaTeX/cache/latex_fcb885f807b78cc36ffeabe9c1627c0e.png" title="\mathcal{C} = \mathcal{D}\times \mathcal{K}" style="vertical-align:-20%;" class="tex" alt="\mathcal{C} = \mathcal{D}\times \mathcal{K}" />. Via its projections, <img src="/extensions/vLaTeX/cache/latex_6ad8e42c94ee85417e3a147612767b08.png" title="\mathcal{C}" style="vertical-align:-20%;" class="tex" alt="\mathcal{C}" /> acts both on <img src="/extensions/vLaTeX/cache/latex_1a9cfd2dbb38672c77272735266aa8b7.png" title="\mathcal{D}" style="vertical-align:-20%;" class="tex" alt="\mathcal{D}" />-spaces and on infinite loop <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spaces. The action of <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> on infinite loop <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spaces leads to a map of monads <img src="/extensions/vLaTeX/cache/latex_63e57f39499c9f102bbd4cd0ce4bfd77.png" title="\alpha\colon C\longrightarrow \Omega^{\infty} \Sigma^{\infty}" style="vertical-align:-20%;" class="tex" alt="\alpha\colon C\longrightarrow \Omega^{\infty} \Sigma^{\infty}" /> and, by adjunction, a right action of the monad <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> on the functor <img src="/extensions/vLaTeX/cache/latex_011bd7c5d63bbc66aa8b463533d65d2a.png" title="\Sigma^{\infty}" style="vertical-align:-20%;" class="tex" alt="\Sigma^{\infty}" />.</p> <p>Ignoring categorical trappings and working with the topology, one proves that for any <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-space <img src="/extensions/vLaTeX/cache/latex_04d0eb37f084cb02c47fa2a271035fef.png" title="X" style="vertical-align:-20%;" class="tex" alt="X" />, the map <img src="/extensions/vLaTeX/cache/latex_be5e47f68ad2269a1c5dede8f1330d3b.png" title="\alpha\colon CX \longrightarrow \Omega^{\infty} \Sigma^{\infty}X" style="vertical-align:-20%;" class="tex" alt="\alpha\colon CX \longrightarrow \Omega^{\infty} \Sigma^{\infty}X" /> is an equivariant group completion when <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" /> is finite. This means that, after passage to <img src="/extensions/vLaTeX/cache/latex_f449ffc7299a0eb49efc51aa509735a7.png" title="H" style="vertical-align:-20%;" class="tex" alt="H" />-fixed points for any subgroup <img src="/extensions/vLaTeX/cache/latex_f449ffc7299a0eb49efc51aa509735a7.png" title="H" style="vertical-align:-20%;" class="tex" alt="H" />, it induces a nonequivariant group completion. The map <img src="/extensions/vLaTeX/cache/latex_35888fd587a5f3b2705b9d0937a89ea5.png" title="\alpha" style="vertical-align:-20%;" class="tex" alt="\alpha" /> is not an equivariant group completion when <img src="/extensions/vLaTeX/cache/latex_3eda8169a35239f3da5653498d0971d9.png" title="G=S^1" style="vertical-align:-20%;" class="tex" alt="G=S^1" />.<br /> So, regrettably, we must restrict attention to finite groups <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />. This also means that we must work as topologists and not category theorists. Nothing whatsoever goes wrong with the formalities in the more general case. One can set everything up in the generality of compact Lie groups. It's just that the actual structure of the fixed point <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spaces works differently for compact Lie groups. I could explain exactly why, but that would be too long for this already too long answer.</p> <p>For a <img src="/extensions/vLaTeX/cache/latex_6ad8e42c94ee85417e3a147612767b08.png" title="\mathcal{C}" style="vertical-align:-20%;" class="tex" alt="\mathcal{C}" />-space <img src="/extensions/vLaTeX/cache/latex_04d0eb37f084cb02c47fa2a271035fef.png" title="X" style="vertical-align:-20%;" class="tex" alt="X" />, for example a <img src="/extensions/vLaTeX/cache/latex_1a9cfd2dbb38672c77272735266aa8b7.png" title="\mathcal{D}" style="vertical-align:-20%;" class="tex" alt="\mathcal{D}" />-space, we can form the <img src="/extensions/vLaTeX/cache/latex_0643966166b879e3e23697a6b846efd7.png" title="G" style="vertical-align:-20%;" class="tex" alt="G" />-spectrum <img src="/extensions/vLaTeX/cache/latex_be6ceac22058ff2749d0e608a5fd47a0.png" title="E X = B(\Sigma^{\infty},C,X)" style="vertical-align:-20%;" class="tex" alt="E X = B(\Sigma^{\infty},C,X)" />. It is a kind of homotopical tensor product of functors that approximates the evident categorical coend <img src="/extensions/vLaTeX/cache/latex_8e44b97bb6e141d545d4992846b2620f.png" title="\Sigma^{\infty}\otimes_C X" style="vertical-align:-20%;" class="tex" alt="\Sigma^{\infty}\otimes_C X" />. Now, sweeping a few technicalities under the rug, one proves as in the nonequivariant case that <img src="/extensions/vLaTeX/cache/latex_12536c600b74e1798cb6c0ed25204c05.png" title="\Omega^{\infty}EX" style="vertical-align:-20%;" class="tex" alt="\Omega^{\infty}EX" /> is a group completion of <img src="/extensions/vLaTeX/cache/latex_04d0eb37f084cb02c47fa2a271035fef.png" title="X" style="vertical-align:-20%;" class="tex" alt="X" />. That's my machine, generalized to the equivariant context.</p> <p>Peter</p> -
- CommentRowNumber28.
- CommentAuthorUrs
- CommentTimeJan 24th 2010
Many thanks, indeed.
I'll digest, and then get back to you.
-
- CommentRowNumber29.
- CommentAuthorMike Shulman
- CommentTimeJan 24th 2010
- (edited Jan 24th 2010)
Me again. I just want to give the definition of a "universal
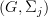 -bundle". In general, the definition of a universal
-bundle". In general, the definition of a universal 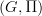 -bundle is a
-bundle is a 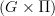 -space E such that for any subgroup
-space E such that for any subgroup 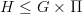 , if
, if 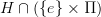 is trivial, then the H-fixed point space of E is contractible, while otherwise the H-fixed point space of E is empty. (There is a yet more general notion for any extension
is trivial, then the H-fixed point space of E is contractible, while otherwise the H-fixed point space of E is empty. (There is a yet more general notion for any extension 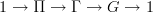 , with
, with 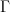 in place of
in place of 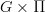 .)
.)The intuition (or, at least, my intution from generalizing the classical case where G is trivial) is that this should should be a G-space with a "free
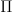 -action" and a "contractible underlying G-space." But I have not yet succeeded in understanding why the above definition is the correct way of capturing that. It certainly implies that the
-action" and a "contractible underlying G-space." But I have not yet succeeded in understanding why the above definition is the correct way of capturing that. It certainly implies that the 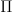 -action is free and the underlying G-space is contractible, but it says more than that too.
-action is free and the underlying G-space is contractible, but it says more than that too.Edit: A big thank-you again to Megan who is doing a great job helping me understand this stuff.
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeJan 24th 2010
- (edited Jan 24th 2010)
So the functors
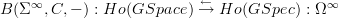
constitute an adjoint equivalence when restricted on the left to grouplike
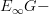 spaces and on the right to connective
spaces and on the right to connective 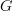 -spectra, in direct analogy to theorem 9.3 p. 29?
-spectra, in direct analogy to theorem 9.3 p. 29? -
- CommentRowNumber31.
- CommentAuthorTim_Porter
- CommentTimeJan 24th 2010
If I may chip in on this. Some 10 years ago Ronnie Brown, Andy Tonks, and Marek Golasinski wrote two papers that looked at some of the analogous things for crossed complexes and worked them through in detail. One was Spaces of maps into classifying Spaces for equivariant crossed complexes, Indagationes Mathematica, 8 (1997) 157-172., the other Spaces of maps into Classifying Spaces for equivariant crossed complexes, II: the general topological case, K-Theory, 23 (2001) 129-155. Given the considerable advances in the last 10 years the general case should be clearish. There was also a homotopy coherent version of Elmendorf that Cordier and I published: Categorical Aspects of Equivariant Homotopy, Proc. ECCT, Applied Cat.Structures.4 (1996) 195-212.
Hope that some of this will be useful. -
- CommentRowNumber32.
- CommentAuthorDavid_Corfield
- CommentTimeApr 3rd 2014
We believe this is the first ∞-categorical approach to equivariant stable homotopy theory,
So says Barwick in Spectral Mackey functors and equivariant algebraic K-theory (I).
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeApr 3rd 2014
I have added a brief paragraph on this to _Mackey functor_ and the same paragraph also to _equivariant stable homotopy theory_.
1 to 33 of 33