nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorTobyBartels
- CommentTimeJan 21st 2010
New page: canonical transformation
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
Any chance you could give some examples as to how this thing reduces to our regular notion of canonicity (canonicalness?)? -
- CommentRowNumber3.
- CommentAuthorTobyBartels
- CommentTimeJan 21st 2010
What is the ‘regular notion’? Do you just mean the informal notion?
There are some in the Usenet discussion linked in the References section.
-
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeJan 21st 2010
I personally do not like the terminology. I mean I do not think that it deserves such a name in category theorem, plus there may be situations where one claims an existence of natural transformations (often just said transformations) and say that this is not only existence but actually those transformations are canonical (there is canonical choice). This is normal and widespread understanding of word canonical hence the hesitation. Plus completely different usage in geometry (canonical transformations in sympletic geometry, Poisson geometry and classical mechanics).
-
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeJan 21st 2010
Is there anyone here in favor of the terminology "canonical transformation"? If not, we could open discussion on what to rename them to. I've proposed "core-natural" as one possibility.
-
- CommentRowNumber6.
- CommentAuthorzskoda
- CommentTimeJan 21st 2010
I like core-natural !
-
- CommentRowNumber7.
- CommentAuthorHarry Gindi
- CommentTimeJan 21st 2010
I'm in favor of reserving judgement on this one for a little bit. Maybe we could ask the guy who came up with it? What if by some small theorem, we can actually recover all of the properties that we want?
-
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeJan 21st 2010
I don't believe here in such a theorem.
-
- CommentRowNumber9.
- CommentAuthorTobyBartels
- CommentTimeJan 21st 2010
If I could do everything from scratch, I would call these things simply ‘natural’; I think that it gets at the intuitive idea of that term. The standard meaning of ‘natural transformation’, while it is the correct notion of morphism between functors, is too specific. That's one reason why I like ‘canonical’ (even though that is a less ideal term than ‘natural’), because it gives the concept its due importance.
I will add some examples to the article and try to motivate the idea that it gets at what it means for a choice to be ‘canonical’ and for an operation to be ‘natural’.
Even if the term ‘canonical’ is desirable, I can see that the phrase ‘canonical transformation’ (which had already appeared on the Lab at momentum, so I added ‘coordinate’ to the middle of the phrase) is not. I don't think that Jim even uses it; I just borrowed the noun from ‘natural transformation’.
For Jim's perspective, here is the individual post in the Usenet thread that justifies the term: #9 (and also #10).
-
- CommentRowNumber10.
- CommentAuthorzskoda
- CommentTimeJan 21st 2010
Word canonical in the mathematics of structures for practical mathematicians means "whose choice may be determined by the data given", i.e. whose existence in some proof or construction can be made such that it avoids arbitrary/voluntary choices (that does not presumes uniqueness, but existence of a preferred, canonical, choice). I can imagine extremely many situations in which we could have Dolan transformations which are and those which are not canonical in this common sense.
-
- CommentRowNumber11.
- CommentAuthorHarry Gindi
- CommentTimeJan 21st 2010
That is the best definition of canonical I've ever heard. Could you put that up on wikipedia? If you'd rather not, would you mind if I did?
-
- CommentRowNumber12.
- CommentAuthorzskoda
- CommentTimeJan 21st 2010
Thanks for the (undeserved) compliments, and of course, I would not mind that you copy it anyplace you like :)
-
- CommentRowNumber13.
- CommentAuthorTobyBartels
- CommentTimeJan 21st 2010
Examples at canonical transformation, basically taken from Jim's Usenet posts.
-
- CommentRowNumber14.
- CommentAuthorHarry Gindi
- CommentTimeJan 21st 2010
@Zoran, to be honest, that was the first time that I've actually been given a satisfying definition of canonical.
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeJan 21st 2010
Back in Oberwolfach last time when Chris Schommer-Pries told me about this concept, I did indeed propose to call it something like "core-natural", too. Chris has proposed "un-natural" :-)
Strictly speaking -- and "core-natural" does indicate this -- there is no new concept here: a "core natural transformation" between two functors is just an ordinarty one between the composites ofboth with the core inclusion.
This is what I had suggested to Chris back then. My feeling was that for instance drawing the relevant diagrams this way, with the core inclusion explicit, also shows better what's going on in his context. I'd think it is of general interest to look at cores of bordisms n-categories. For instance the path infinity-groupoid of a space X that I like to go on about is a lot like part of the core of n-cobordisms in X. (or something like that).
-
- CommentRowNumber16.
- CommentAuthorTobyBartels
- CommentTimeJan 21st 2010
- (edited Jan 21st 2010)
Zoran's definition, while impeccable, is not a definition in any mathematical sense (nor do I think that he intended it to be one). I don't see why it's OK to formalise ‘natural’ but not ‘canonical’.
Actually, ‘natural’ in common usage might not only mean canonical but also functorial.
Do we have a word for a functor from the core of a category C to another category D? That is the most general non-evil concept of an operation that maps an object of C to an object of D, and a canonical transformation (or equivalently natural transformation, since we already introduced the core of C) between such functors is the most general non-evil concept of an operation that maps an object of C to a morphism of D.
-
- CommentRowNumber17.
- CommentAuthorMike Shulman
- CommentTimeJan 22nd 2010
Do we have a word for a functor from the core of a category C to another category D?
"core-functor"? (-:
I think some people might say that 'natural' shouldn't have been formalized, but given that it was, we're stuck with it, but there's no reason to compound the problem.
I don't like "un-natural" because they are partly natural. To me "un-natural transfomation" suggests a transformation that satisfies no naturality properties at all, such as appear in the internal-hom associated to the "funny tensor product" on Cat.
-
- CommentRowNumber18.
- CommentAuthorHarry Gindi
- CommentTimeJan 22nd 2010
Is that like a "funny uncle"? -
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeJan 22nd 2010
- (edited Jan 22nd 2010)
I don't like "un-natural"
I guess I wasn't being clear: I didn't mean to suggest the term "un-natural", I just mentioned it as an example that also Chris was struggling to find a good term. I don't favor this term at all. I like "core-natural". But maybe what I prefer most would be no extra term, but just the more lengthy but clear "transformation of functors restricted to the core".
By the way: many thanks to Toby for digging out Jim Dolan's motivating examples. For the very first one I can see where the term "canonical" came from, but then for the next ones already it begins to feel like a stretch. But it is good to see what was going on in Jim's mind back then.
-
- CommentRowNumber20.
- CommentAuthorHarry Gindi
- CommentTimeJan 22nd 2010
If you didn't get my reference, it's alright. It's a reference to child molestation in the 1950s, where abuse was committed by a family member (stereotypically an uncle). It's just that in the 1950s, people also tried to deal with these types of things without going to the police, so a lot of abuse went unpunished etc. Whence came the term "funny uncle", where funny doesn't mean funny like Uncle Joey (John Stamos) from full house. It's just that whenever I see the word 'funny' in full quotes like that, I have to make that joke. -
- CommentRowNumber21.
- CommentAuthorTobyBartels
- CommentTimeJan 22nd 2010
My problem with ‘core-natural’ is that (like ‘extranatural’, for that matter) it downplays the importance of the thing.
@ Urs #19
Actually, I thought that the commutative of ordinal addition was the strongest example; how could the commutativity isomorphism not be canonical?
@ All:
How about just ‘transformation’? In general, a transformation is an operation from the objects on one category to the morphisms of another; but if this operation is not evil, then it ought to be a canonical transformation between two, well, core-functors.
-
- CommentRowNumber22.
- CommentAuthorMike Shulman
- CommentTimeJan 22nd 2010
I am entirely happy with downplaying the importance of the thing. Jim's examples are all "cute" rather than having any real meaning or use in mathematics. Chris' characterization is the only real application of these things that I have ever seen. Contrast this with extranatural transformation that occur all over the place.
I think "transformation" is bad because it is commonly used with an unspoken "natural" in front. Like it or not, I think by now the default meaning of "transformation" in category theory is a natural one.
-
- CommentRowNumber23.
- CommentAuthorTobyBartels
- CommentTimeJan 22nd 2010
Well, you're pretty much defining these things to be invisible. They capture the intuitive meaning of ‘natural’, but that's taken. At least that is merely an adjective, but now the noun is also forbidden? So even ‘core-natural transformation’ and ‘extranatural transformation’ are only allowed by the red herring principle? I cannot agree with that.
Do you seriously believe that the commutativity of ordinal addition of finite well-ordered sets is cute but useless? I have trouble buying that.
And the fact that natural transformations and dinatural transformations (including extranatural transformations) are both examples of one concept is also cute but useless? Even if there were no natural examples that didn't fall into one or the other of those classes, that is already meaningful to me.
More broadly, I'm surprised that you want to change the name of something as soon as it appears on the Lab. At least Jim himself did not write it, and will not advise him to.
-
- CommentRowNumber24.
- CommentAuthorMike Shulman
- CommentTimeJan 23rd 2010
I don't buy that 'canonical' transformations capture 'the' intuitive meaning of 'natural.' I don't think there is any one intuitive meaning of 'natural'. And I'm not sure what your point is about adjectives and nouns.
The commutativity of ordinal addition of finite well-ordered sets is certainly important, but it is encapsulated by saying that the groupoid of finite well-ordered sets is symmetric monoidal (which is, of course, just saying that N is a commutative monoid). Which is why 'core-natural' is good—it makes it clear that, as Urs said, there isn't really a new concept, just an application of an old one in a modified context.
And the fact that natural transformations and dinatural transformations (including extranatural transformations) are both examples of one concept
Natural transformations and dinatural transformations both have underlying 'canonical' transformations, but I wouldn't say that's the same as saying they are both examples of them. They both have underlying totally-unnatural transformations too.
Perhaps 'cute but useless' was too strong a phrase (I was in a hurry). I agree that these things are interesting and meaningful, but I don't think they need a new word, when we can instead call them something like 'core-natural' which (a) is more descriptive and suggestive and (b) doesn't steal yet another word commonly used with various informal meanings for a particular precise meaning that may or may not capture one of those informal meanings.
More broadly, I'm surprised that you want to change the name of something as soon as it appears on the Lab.
I'm a bit confused—what does its recent appearance on the Lab have to do with it? We just learned about these things, and so we're having a discussion about what to call them. Jim called them one thing in an unpublished usenet discussion 16 years ago, but we've frequently exhibited a willingness to replace terminology that's in much more widespread and established use than that—especially if, as you said, Jim never put together 'canonical' and 'transformation'. Would it be better to leave up the page with one name for a long time before starting to discuss whether to change it? If we are going to change it, we should change it as soon as possible, so that more people read about it with our chosen name.
More and more, it seems to me that everyone is eager to change other people's terminology that they dislike, but outraged when anyone else suggests changing the terminology that they like. (-: I'm that way just as much as anyone else, of course.
-
- CommentRowNumber25.
- CommentAuthorTobyBartels
- CommentTimeJan 25th 2010
I don't think there is any one intuitive meaning of 'natural'.
Well OK, ‘the’ is too strong a word. But it captures the intuitive sense of ‘natural’ as it appeared in pre-categorial literature (and still appears in extra-categorial literature) which is partially captured by ‘natural transformation’. In particular, Jim's examples of canonical (but not natural) transformations are just as ‘natural’ (‘basis-free’, ‘coordinate-independent’, ‘generally covariant’) as the natural transformation from a vector space to its double dual.
Natural transformations and dinatural transformations both have underlying 'canonical' transformations, but I wouldn't say that's the same as saying they are both examples of them.
This may be another appearance of one of our philosophical differences: I don't see a great distinction between ‹extra property› on the one hand and ‹extra structure›, ‹extra stuff›, etc on the other hand. What I mean is that the various transformations are all canonical transformations with extra bells and whistles (to quote John).
They both have underlying totally-unnatural transformations too.
What is a ‘totally-unnatural transformation’? If you mean a family of morphisms of D, indexed by the objects of C, where the morphism indexed by x is from F(x) to G(x), then I don't think that this is a very coherent notion. Are there any useful and interesting examples of these that are not canonical transformations?
I had more to say about that, but it may not matter, since you have said
I agree that these things are interesting and meaningful
so that is OK.
Jim called them one thing in an unpublished usenet discussion 16 years ago
Jim doesn't only use it in that thread. In fact, I'd never read that thread until I searched for references for the article, but I'd seen it in other posts online and heard him use it in conversation. Like Grothendieck, Jim doesn't publish his work.
we've frequently exhibited a willingness to replace terminology that's in much more widespread and established use than that
I've wanted to tweak terminology when I think that the idea isn't quite right, but I don't think that this situation applies here.
everyone is eager to change other people's terminology that they dislike, but outraged when anyone else suggests changing the terminology that they like.
Ha, yes. (^_^)
I think that I was mostly outraged at the suggestion that the idea was only ‘cute’. Now I am no longer outraged.
-
- CommentRowNumber26.
- CommentAuthorTobyBartels
- CommentTimeJan 25th 2010
I've rewritten the Idea section to downplay the idea that these really capture the meaning of ‘canonical’, focussing instead on the question of whether natural transformations really capture the meaning of ‘natural’. I also introduce the term ‘core-natural’ here (and repeat it later). I moved the Warnings up (the reason for having them as low as they were is obsolete and was probably silly anyway). Finally, I added another example; all of the previous examples were isomorphisms but this one is not. (But it is probably the most strained example.)
-
- CommentRowNumber27.
- CommentAuthorTobyBartels
- CommentTimeJan 25th 2010
By email, Jim suggests ‘canonical map’ or ‘canonical morphism’ to avoid bumping into ‘canonincal transformation’ in the sense from geometry and physics.
-
- CommentRowNumber28.
- CommentAuthorMike Shulman
- CommentTimeJan 27th 2010
I just want to continue being able to say "canonical" to mean "determined in a standard way from the data given," e.g. canonical topology on a category, canonical model structure on Cat, without feeling like the word has been taken over officially for some precise but rarely-used notion that doesn't include the way I am used to using it.
Like Grothendieck, Jim doesn't publish his work.
With all due respect to Jim and Grothendieck and other people who don't publish their work, I think there's a reason that the mathematical community expects work to be published if one wants it to be properly credited and respected.
-
- CommentRowNumber29.
- CommentAuthorDavidRoberts
- CommentTimeJan 27th 2010
(place tongue in cheek)
I don't publish my work either :) can I be mentioned in the same sentence as Grothendieck?
(remove tongue from cheek)
Speaking more seriously, I would be interested to see more write-up of Jim's work on the nLab (or Jim's web, or John's web) - as Urs noted when the lab was set up, he didn't want gems and brilliant insights from blog comments lost in the mists of time (compare: old newsgroup stuff that can still be found, but is little known, as we have seen recently). Though I guess this would take possibly a considerable effort, and we are all still working on our own stuff...
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
I don't publish my work either :) can I be mentioned in the same sentence as Grothendieck?
I had had the same association. But wouldn't you say that Grothendieck, while not publishing along the traditional road, made sure that his work was being communicated, be it via lengthy telegrams to colleagues, or be it by talking to his prolific students?
By the way, I once created a web for Jim Dolan in the vague hope that he might enjoy using it as a notepad. John seems to have tried to support this, but I never heard back anything on this from either of them.
-
- CommentRowNumber31.
- CommentAuthorTobyBartels
- CommentTimeJan 27th 2010
- (edited Jan 27th 2010)
@ Mike
I just want to continue being able to say "canonical" to mean "determined in a standard way from the data given," e.g. canonical topology on a category, canonical model structure on Cat, without feeling like the word has been taken over officially for some precise but rarely-used notion that doesn't include the way I am used to using it.
But you still use ‘natural’ in a nontechnical sense (example). So why is ‘canonical’ threatened?
@ David (& Urs similarly)
I would be interested to see more write-up of Jim's work on the nLab (or Jim's web, or John's web)
Yeah, so would I. I was obliquely referring to that at the end of comment #23; this discussion is exactly the sort of thing that he doesn't want to deal with. But why not on his personal web? He and John started to write about algebraic geometry, but it didn't happen. I'm supposed to talk to Jim this evening, so I'll remind him of its existence and see if I can't get more of a response out of him.
-
- CommentRowNumber32.
- CommentAuthorTobyBartels
- CommentTimeJan 27th 2010
I put in a definition of the term ‘canonical morphism’ as such.
Possibly the article would work better if we start with that as the main concept, only later combining the canonical morphisms into a single canonical/core-natural transformation.
-
- CommentRowNumber33.
- CommentAuthorDavidRoberts
- CommentTimeJan 27th 2010
I suppose if Jim finds publicly exposing his work in progress his web could be private, and John could port stuff that is a bit more polished to his own web - but this is just a suggestion.
-
- CommentRowNumber34.
- CommentAuthorTobyBartels
- CommentTimeJan 28th 2010
@ David #33
That's almost how it was set up (except that Jim's is published, not quite private), and that's how they did one article, but they didn't continue. I'll ask Jim about it tonight.
-
- CommentRowNumber35.
- CommentAuthorMike Shulman
- CommentTimeJan 28th 2010
But you still use ‘natural’ in a nontechnical sense (example). So why is ‘canonical’ threatened?
If I may graciously quote myself:
some people might say that 'natural' shouldn't have been formalized, but given that it was, we're stuck with it, but there's no reason to compound the problem.
(-:
-
- CommentRowNumber36.
- CommentAuthorTobyBartels
- CommentTimeJan 28th 2010
And my claim is that formalising ‘natural’ has not caused a problem, as shown by the fact that you (and I, and others) continue to use it informally, and this rarely causes confusion.
(The problem would be if somebody wants to formalise it in a different way in a similar context.)
-
- CommentRowNumber37.
- CommentAuthorMike Shulman
- CommentTimeJan 28th 2010
Looking at the example of endomorphisms of a 2-element set again, I like the concept more but still not the terminology. To me 'canonical' implies something determined uniquely by the given structure, which is certainly not the case here, since there can be multiple distinct 'canonical transformations' between two functors. I think I can now see the argument that these morphisms capture one intuitive sense of 'natural', but unfortunately that word is taken. (-:
To me the defining property of these things seems to be that they are "non-arbitrary" or "choice-free." Apparently "nonarbitrary" is actually in the dictionary, but it's kind of an ugly word. Actually, I think one sensible thing to call these, especially looking at the case of single morphisms, would be equivariant: a morphism from F(x) to G(x) is 'canonical' just when it is equivariant w.r.t. the actions of the group Aut(x) on either side.
-
- CommentRowNumber38.
- CommentAuthorTobyBartels
- CommentTimeJan 28th 2010
To me 'canonical' implies something determined uniquely by the given structure
But that doesn't fit with your own examples, such as the canonical topology on a category. There are other Grothendieck topologies on most categories, after all.
I think that Jim has used ‘coordinate-free’, ‘basis-independent’, and the obvious other two phrases as related terms (but with a more limited scope). I like ‘equivariant’, but it is used pretty widely, so I worry about clashes.
-
- CommentRowNumber39.
- CommentAuthorHarry Gindi
- CommentTimeJan 28th 2010
- (edited Jan 28th 2010)
The canonical grothendieck topology is given by a universal property! I asked a question on MO within the past month about exactly that, and I translated and wrote up the relevant page of SGA.
-
- CommentRowNumber40.
- CommentAuthorzskoda
- CommentTimeJan 28th 2010
Where is that translation now ? Is it in nlab ?
-
- CommentRowNumber41.
- CommentAuthorMike Shulman
- CommentTimeJan 29th 2010
The canonical topology is not the unique topology, but it is the unique topology which contains all other topologies for which the representables are sheaves. In that sense it is determined uniquely. By contrast there can be many 'canonical' transformations between two given functors with nothing to single out any of them.
"Equivariant" is used pretty widely, but I'm only aware of one basic meaning, namely respecting the actions of some group. Are there others?
-
- CommentRowNumber42.
- CommentAuthorDavidRoberts
- CommentTimeJan 29th 2010
- (edited Jan 29th 2010)
I'm reminded of the quote from Through the Looking Glass
"When I use a word," Humpty Dumpty said, in rather a scornful tone, "it means just what I choose it to mean -- neither more nor less."
"The question is," said Alice, "whether you can make words mean so many different things."
-
- CommentRowNumber43.
- CommentAuthorHarry Gindi
- CommentTimeJan 29th 2010
- (edited Jan 29th 2010)
For Zoran:
http://mathoverflow.net/questions/11069/induced-grothendieck-topology-on-a-presheaf-or-sheaf-category-of-a-site/11222#11222
It's given by a universal property on the category of sheaves on a site, so I would say that it's the canonical topology for a Grothendieck topos. My translation wasn't as extensive as I'd previously thought, but between my answer and Clark's you should get the gist of it. -
- CommentRowNumber44.
- CommentAuthorTobyBartels
- CommentTimeJan 29th 2010
- (edited Jan 29th 2010)
The canonical topology is not the unique topology, but it is the unique topology which contains all other topologies for which the representables are sheaves. In that sense it is determined uniquely. By contrast there can be many 'canonical' transformations between two given functors with nothing to single out any of them.
Yes, the canonical topology is not the unique topology, but it is the unique topology satisfying a certain property.
Similarly, the non-identity canonical morphism
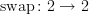 is not the unique morphism
is not the unique morphism 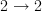 , but it is the unique morphism satisfying a certain property. (There are many ways to state this property: it is a derangement, it is not the identity, it is equal to
, but it is the unique morphism satisfying a certain property. (There are many ways to state this property: it is a derangement, it is not the identity, it is equal to 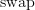 , etc.) Also, the canonical transformation
, etc.) Also, the canonical transformation  is not the unique canonical transformation
is not the unique canonical transformation 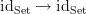 , but it is the unique transformation satisfying a certain property.
, but it is the unique transformation satisfying a certain property.In contrast, the two noncanonical morphisms
 cannot be characterised uniquely using non-evil language (although that is hard to make precise).
cannot be characterised uniquely using non-evil language (although that is hard to make precise).The best sense that I can make of what you're saying here is that ‘canonical’ should only come after ‘the’, never after ‘a’. In any given situation, we may (if we wish) state some property that is satisfied by at most one thing, and declare that thing to be ‘canonical’. We can do this completely arbitrarily, as long as the thing that we pick is uniquely determined by the data at hand, but we can only do it once. So it doesn't make sense to define ‘canonical’ in general, since then there are many situations in which we have chosen canonical things. Instead, we must use a family of ad hoc definitions, to pick (at most) one thing out in each context. Is this what you mean?
If so, my reply is that the general notion of ‘canonical’ is used in a grammatically different way (following ‘a’, not ‘the’) which should not cause confusion; but it is related, since only a canonical thing can be uniquely specified by the data at hand so that you can define it to be the canonical thing.
"Equivariant" is used pretty widely, but I'm only aware of one basic meaning, namely respecting the actions of some group. Are there others?
Not that I know of, but the concept of canonical morphism applies in a more specific situation, when one automorphism group acts (on both sides) on another via a couple of functors. I'm worried that ‘equivariant morphism’ (a term which certainly exists already) might be applied to some other group actions in this situation. But perhaps there are no other group actions likely to be thought of.
-
- CommentRowNumber45.
- CommentAuthorTobyBartels
- CommentTimeJan 29th 2010
On second thought, if you simply have two actions/representations of a group
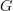 on objects of a category
on objects of a category  , then this is two functors from
, then this is two functors from 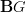 to
to  , and a canonical morphism between these is precisely a
, and a canonical morphism between these is precisely a 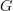 -equivariant morphism between the original representations of
-equivariant morphism between the original representations of  . The general concept is a straightforward generalistion of this. So there probably is no room for confusion.
. The general concept is a straightforward generalistion of this. So there probably is no room for confusion. -
- CommentRowNumber46.
- CommentAuthorMike Shulman
- CommentTimeJan 30th 2010
The best sense that I can make of what you're saying here is that ‘canonical’ should only come after ‘the’, never after ‘a’.
Yes, that's about what I meant.
If so, my reply is that the general notion of ‘canonical’ is used in a grammatically different way (following ‘a’, not ‘the’) which should not cause confusion
I disagree that it should not cause confusion; I already find it confusing. It also seems to me that in natural language, canonical always does come after 'the'.
-
- CommentRowNumber47.
- CommentAuthorTobyBartels
- CommentTimeJan 31st 2010
It also seems to me that in natural language, canonical always does come after 'the'.
Well, that statement seems easy to refute (not all hits are relevant, but some seem to be).
Actually the Wikipedia hit seems very much to agree with me (although I had no hand in writing it, which is sometimes the reason). It reminds us in particular of the Jordan canonical form of a matrix, which is surely a canonical form but not the canonical form. (As such, this is an example of a functor rather than a transformation, of course.)
-
- CommentRowNumber48.
- CommentAuthorMike Shulman
- CommentTimeFeb 1st 2010
Sigh.
I appear to be completely failing to communicate my point. (No, I didn't mean that the word "canonical" literally always follows "the".) If there's anyone else still listening to this discussion, do you have any idea what I'm trying to say?
Wherever I have seen "canonical" used in mathematics (or elsewhere, except for the Ubuntu software company), it refers to something which is determined uniquely by the construction of something, or by some natural (in the non-technical sense) or desirable requirement. (I have never encountered Wikipedia's supposed specific meaning of "coordinate-free.") Anything you can describe can of course be determined uniquely by some requirement, namely that it be equal to the thing described by that description, but that doesn't make it canonical. There is also definitely a role of societal convention in deciding what is canonical and what isn't.
If I'm interested in studying topologies on categories for which the representables are sheaves, then naturally the "canonical" topology will play an important role. There are other topologies that exist on every category and can be defined "globally," such as the trivial topology or the atomic topology or the largest topology for which the representables are separated, but we don't call those "canonical," because, well, we don't. We either have other names for them (like "trivial") or we don't talk about them enough to merit having their own names. When I construct the quotient of a group by a normal subgroup, the "canonical" homomorphism (as referenced by Wikipedia) is determined by the definition of the quotient group as a set of equivalence classes in the group itself, or if you're a category theorist, by the universal property it satisfies. The Jordan canonical form is a particularly nice form for any matrix; obviously it's not the only "form" into which every matrix can be put (just like there are more topologies on a category than the "canonical" one), but matrix theorists have decided that it's important enough to call "canonical," maybe with Jordan's name in front to disambiguate.
The set-theoretic usage mentioned at the end of the Wikipedia section also fits this usage, but seems to be diametrically opposed to the notion of 'equivariant transformation'. Once you've chosen a representative of each equivalence class, you can declare that representative to be canonical (societal convention again, this time in a "for the noonce" form rather than globally). But choosing an element out of a collection of sets is exactly what you're saying can't be done 'canonically.'
-
- CommentRowNumber49.
- CommentAuthorDavidRoberts
- CommentTimeFeb 1st 2010
I agree with you, Mike.
I use canonical myself when referring to the existence of something (like a functor) that is the 'obvious and best' choice, something that falls into my lap, so to speak, even though it may be defined up to isomorphism/equivalence. In other words, it is not really a choice because a) it should be obvious (to a practitioner) and b) any other such object requires additional (arbitrary) choices, possibly using AC, in its construction/definition. It seems to me to be similar to having a completely presented set - technical use of AC is not an issue because there is an obvious choice, indicated either conceptually or syntactically (in a non-technical sense, more like 'write down the obvious formula'). -
- CommentRowNumber50.
- CommentAuthorTobyBartels
- CommentTimeFeb 1st 2010
I appear to be completely failing to communicate my point.
Yes, it seems like you and I are completely failing to communicate, Mike. Most of your last message makes almost no sense to me in the context of the preceding discussion, and it is as clear to me that you don't understand what I'm trying to say and the reverse seems to be clear to you.
maybe with Jordan's name in front to disambiguate
For what it's worth, I agree that I can't possibly be understanding you, since the need to disambiguate here seems to undermine your position. (In fact, I presumably just have no idea what your position is.)
Anyway, I will work on the article a bit more this week, and you can tell me what you think of it then.
-
- CommentRowNumber51.
- CommentAuthorHarry Gindi
- CommentTimeFeb 1st 2010
- (edited Feb 1st 2010)
>_> Conical transformation. Why are we arguing about cones? -
- CommentRowNumber52.
- CommentAuthorTobyBartels
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
I've reworked the article to focus on canonical morphisms as the primary concept, making the link both to natural transformations on the one hand and to intertwiners on the other. (I still have to go through the section of Examples.)
-
- CommentRowNumber53.
- CommentAuthorHarry Gindi
- CommentTimeFeb 2nd 2010
I think that the way the definition as currently stated is evil, but I can't really put my finger on why. -
- CommentRowNumber54.
- CommentAuthorTobyBartels
- CommentTimeFeb 2nd 2010
That's funny, since the idea should be precisely what is not evil. So if you put your finger on it, then please let me know!
For the record, the context of the definition of canonical morphism consists of the variables C, D, F, G, and x (typed as indicated there).
-
- CommentRowNumber55.
- CommentAuthorHarry Gindi
- CommentTimeFeb 2nd 2010
- (edited Feb 2nd 2010)
I guess because we're specifying an object x, which seems somewhat strict to me. I mean, as stated, this is just a map of group actions of Aut(x). The problem I have with putting it into all of this categorical language is that it doesn't seem like the concept of a canonical transformation generalizes well to higher categories, and it's just a lot more complicated. -
- CommentRowNumber56.
- CommentAuthorTobyBartels
- CommentTimeFeb 2nd 2010
You missed out G. In any case, it's not the canonical morphism that is a represenation of the group Aut(x) but rather F and G which are; then the canonical morphism is an intertwiner between these representations.
However, Jim typically uses the term when F and G are entire functors, defined on all of C rather than just on x and Aut(x). Then there is no standard term for it (other than ‘intertwiner between the induced representations of Aut(x)’).
-
- CommentRowNumber57.
- CommentAuthorTobyBartels
- CommentTimeFeb 3rd 2010
Re #52: Now also the examples have been redone.
-
- CommentRowNumber58.
- CommentAuthorChris SchommerPries
- CommentTimeNov 4th 2010
I know this thread is mostly dead, but I just discovered it and want to throw a few more coins into the wishing well. Somewhere along the line Urs mentioned how I had discovered this and related concepts in the wild and suggested the name “unnatural transformation”. This was at an Olberwolfach conference. Mainly, this was a wild suggestion to a friendly audience, mostly meant to stir up discussion and generate ideas about better terminology. I think I also suggested “supernatural transformation”. Neither of these are very satisfying, in my opinion. I think Jim’s canonical transformation, which I learned about later, is much better.
I also like the term “subtransformation”. Especially so because “transformation” seems to be identified with “natural transformation” in many people’s minds. So if you just use an adjective, like “canonical” or “unnatural” or “core”, to modify transformation people might be confused that this is some sort of special kind of natural transformation, when in reality the opposite is true.
In the examples I was considering there were two important aspects. One was the filtration (which for the sake this discussion is the inclusion of the core). But the other is the importance of lax transformations. For a long time I’ve been stuck with this project because I didn’t know how to deal with lax transformation in a model invariant, (infinity, n)-manner. I think I’ve finally come to grips with later point and am ready to return to the first aspect. Whence I discovered this thread.
It seems like you can define these sort of “less than natural” transformations (and higher generalizations) whenever you have an n+1 step filtration of your n-category (I remember talking to Urs about this way back in Olberwolfach. He may have suggested it to me). So a traditional natural transformation would correspond to the trivial constant filtration, while Jim’s canonical transformation would correspond to the core filtration. In general you have something more exotic. The inclusionary aspect of the filtration seems to jive with the “sub” of “subtransformation”, which I find pleasant. Another term which has been suggested to me is “subnatural transformation”, which shares many of these benefits.
I’m very curious to hear people’s opinions on this. This is a chance to create a new piece of terminology and I think it is important to try to get it right at the beginning.
-
- CommentRowNumber59.
- CommentAuthorDavidRoberts
- CommentTimeNov 4th 2010
Subnatural sounds good to me.
-
- CommentRowNumber60.
- CommentAuthorTobyBartels
- CommentTimeNov 4th 2010
I prefer ‘subnatural transformation’ to ‘subtransformation’, although I think that ‘core-natural transformation’ is even clearer. We shouldn’t have problem with the red herring principle here, since ‘core’ is clearly modifying ‘natural’ (or at least it’s clear to me!).
What is the more general concept? A ‘filtered-natural transformation’?
-
- CommentRowNumber61.
- CommentAuthorMike Shulman
- CommentTimeNov 4th 2010
It seems to me that "core-natural transformation" exactly captures what's going on from the filtration viewpoint: it's a transformation which is natural when restricted to the core. If you have an arbitrary subcategory in mind that isn't necessarily the core, then I think "subnatural transformation" makes sense: a transformation which is natural when restricted to a fixed subcategory. -
- CommentRowNumber62.
- CommentAuthorUrs
- CommentTimeNov 4th 2010
- (edited Nov 4th 2010)
if it is the case that the filtration is always by a genuine sub--category then strictly speaking there is no real need for a new term, since a subnatural transformation is just a natural transformation .
I felt and still feel that this is the best way to go about it – if it is true in your examples that the filtration is always by a genuine sub-category.
Notably I feel that thinking about natural transformations suggests more vividly to us that there is something to be understood here, conceptually: instead of just giving this construction a name and moving on, we should ask ourselves what it is here that should make us want to define transformation between TFTs after restricting them.
Not sure if you have seen it, but not long ago I created that entry titled (grandiosely so and intentionally in this case ;-) holographic principle of higher category theory which is about the nature of transformations between -functors between -categories of cobordisms.
For the kind of story that this entry tries to tell, it would be of great interest to have a general abstract reason for why one would want to consider transformations only after restriction.
I mean, I understand well that one good reason is that this way the result is interesting. But there should also be a good a priori-reason for it.
-
- CommentRowNumber63.
- CommentAuthorTobyBartels
- CommentTimeNov 5th 2010
strictly speaking there is no real need for a new term, since a subnatural transformation is just a natural transformation
Sure, we’ve already noticed that with core-natural transformations. But you still want some term; a ??? .
-
- CommentRowNumber64.
- CommentAuthorUrs
- CommentTimeNov 5th 2010
- (edited Nov 5th 2010)
I guess what I am saying is that in the context in which this arises in Chris’s application, it might be more worthwhile to call and themselves by their proper name. Why is it that we may want to restrict an -dimensional extended QFT this way? Where does this come from abstractly? If this were identified, we’djust speak of a transformation between these restrictions.
Here is maybe a hint: for 3d TQFT we know what it means to consider the restriction along to invertible 3-morphisms. That’s essentially what’s called the “modular functor” on surfaces. That plays a big role in existing theory. Maybe it would be useful to understand the generalization of this notion for any -d QFT. Then the “supernatural transformations” that we are talking about might be just called “transformations between the modular -functors underlying given -functors”. That would seem to me to be a more insightful terminology.
1 to 64 of 64