nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 23rd 2010
as promised (to Domenico), a stub for characteristic class
-
- CommentRowNumber2.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 23rd 2010
- (edited Jan 23rd 2010)
:-)
the Lab seems to be down (or at least I'm unable to connect to), so I'll try to have a look at characteristic class later. In the meanwhile I can remember that in the entry cohomology there's the " is a group object --> is a group" remark, with the " for abelian " example. maybe one could go one step further: " is a ring object --> is a ring", with the " for a commutative ring " example. -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 23rd 2010
yes, right.
if you want to do me a big favor, you should just go ahead and implement such things. I will not run the risk of feeling bored, if you help me out a bit with typing! on the contrary, it would be a relief. don't feel shy about it, you can't break anything.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeJan 23rd 2010
the Lab seems to be down
Yes, the lab is down, apparently. Unfortunately I myself still don't have access to the new server. I emailed Andrew and Toby about it. Hopefully one of them can restart it soon.
-
- CommentRowNumber5.
- CommentAuthorTobyBartels
- CommentTimeJan 23rd 2010
It is back.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeJan 23rd 2010
maybe one could go one step furthermaybe one could go one step further
Okay, I edited a bit more
This is not and is not meant to be anywhere close to perfect. Please don't hesitate to further improve.
I also started an examples-section
-
- CommentRowNumber7.
- CommentAuthorDavidRoberts
- CommentTimeJan 24th 2010
An example of characteristic classes that I would like to see put up (I don't have time at the moment, so this is as much a reminder for me as well as a provocation for anyone else) is that introduced by Murray-Vozzo in the article The caloron correspondence and higher string classes for loop groups. In particular, the last paragraph poses the question as to what geometric significance these classes have. Personally I think they have something to do with classifying Lie oo-groupoids, in the guise of NQP-manifolds or something like that, but that is just intuition. -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeJan 24th 2010
- (edited Jan 24th 2010)
Thanks, David, good point.
I need to remind myself of some details in that article, but not tonight.
But I think this should be easily describebable very generally.
The main point is that of transgression of cocycles, which has, I think, a very simple interpretation in the abstract picture, too:
for
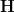 an (oo,1)-topos, we have described in some detail now that the hom-functor
an (oo,1)-topos, we have described in some detail now that the hom-functor 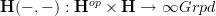 is on objects the cohomology oo-groupoid.
is on objects the cohomology oo-groupoid.So the obvious question is: what is it applied to morphisms?
And I think the answer is: if we take it to be enriched over itself
![[-,-] : \mathbf{H}^{op} \times \mathbf{H} \to \mathbf{H} [-,-] : \mathbf{H}^{op} \times \mathbf{H} \to \mathbf{H}](/extensions/vLaTeX/cache/latex_54791d194e142d553174c7e313803ed4.png)
(in entire analogy to how sheaf categories are cartesian closed)
then applied to a morphism in the second argument, i.e. applied to a cocycle, this is transgression :
so for
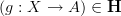 an A-cocycle on X, and for
an A-cocycle on X, and for 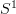 the circle, say, we get the loop spaces
the circle, say, we get the loop spaces ![[S^1,X] [S^1,X]](/extensions/vLaTeX/cache/latex_c1ccbd843ca590d3b2a53a499fd062d7.png) and
and ![[S^1, A] [S^1, A]](/extensions/vLaTeX/cache/latex_432349007fd30322ff974f031962a165.png) and a cocycle on the first with coefficients in the other
and a cocycle on the first with coefficients in the other![[S^1,g] : [S^1,X] \to [S^1,A] [S^1,g] : [S^1,X] \to [S^1,A]](/extensions/vLaTeX/cache/latex_daf35ed9d3dfcf160e2a6f4ec1a68715.png)
This is the transgressed cocycle, essentially.
I'd think this is the main mechanism in considerations such as the Caloron-article, up to some variations.
That just as a quick remark. Maybe more on this tomorrow.
-
- CommentRowNumber9.
- CommentAuthordomenico_fiorenza
- CommentTimeJan 24th 2010
@Urs: I know, and I'm sorry of not being implementing additions myself these days. but I'm totally busy with students this period (fall term examinations..) and the only thing I'm able to do now is to give a quick look at the forum and eventually sketch some stubby idea, sorry for that. From mid-February on I'll be actively back on the lab pages :-) -
- CommentRowNumber10.
- CommentAuthorzskoda
- CommentTimeJan 25th 2010
- (edited Jan 25th 2010)
While the discussion of the name 'characteristic class' is plausible, it is unfortunately not true. The continuous map into the classifying space, by which the pullback of a universal class gives the characteristic class of a manifold is traditionally called the characteristic map because that map characterizes that cohomology class. It is not the cohomology THEORY which is characterized by that map, but the very CLASS. So characteristic classes are those which can be characterized by the maps to given classifying space.
-
- CommentRowNumber11.
- CommentAuthorDavidRoberts
- CommentTimeJan 25th 2010
In other words, given a classifying space, it gives rise to characteristic classes, by pulling back classes along maps to the space -- but do all characteristic classes (which are defined without reference to a fixed space) arise as pulled-back classes from a classifying space? -
- CommentRowNumber12.
- CommentAuthorAndrew Stacey
- CommentTimeJan 25th 2010
(Jumping in late so may have missed subtleties which render this useless.)
Yes - because the characteristic classes must also exist on the classifying space and therefore sit there as self-maps of the classifying space just waiting to be pulled back to arbitrary spaces.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeJan 25th 2010
wait, are you asking me to change the wording somewhere? The characteristic class induced by a cocycle
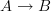 on a cocycle
on a cocycle 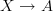 and the bundle
and the bundle 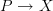 it classifies is the class of the composite
it classifies is the class of the composite 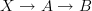 . That's what I mean to say. If I said it differently, that's by mistake.
. That's what I mean to say. If I said it differently, that's by mistake. -
- CommentRowNumber14.
- CommentAuthorzskoda
- CommentTimeJan 25th 2010
I was complaining that the sentences
This serves to characterize cohomology with coefficients in a complicated object A by a collection of cohomology classes with simpler coefficients. Therefore the name characteristic class .
misrepresent the history and the standard motivation for the word characteristic in this context. The rest is perfectly OK and correct. I opened the query box in characteristic class with a suggestion how to resolve this historical note. I may be wrong, though I am about 95% sure that I told the correct story.
-
- CommentRowNumber15.
- CommentAuthorzskoda
- CommentTimeMar 22nd 2011
- (edited Mar 22nd 2011)
New entry Gel’fand-Fuks cohomology (usually studied in connection to some characteristic classes, like those of foliations).
-
- CommentRowNumber16.
- CommentAuthorjim_stasheff
- CommentTimeMar 24th 2011
As characteristic classes of principal bundles indicates, such classes were historically
meant to (parially) characterize something - in this case bundles
To generalize it to the extent indicated in the exposition we are discussing
is to lose the meaning almost totally - OK in physspeak but in math??? -
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeMar 24th 2011
- (edited Mar 24th 2011)
The meaning is kept exactly. In every oo-topos, every morphism of the form is a characteristic class that sends -principal -bundles to a characteristic class in degree -cohomology.
-
- CommentRowNumber18.
- CommentAuthorzskoda
- CommentTimeMar 24th 2011
Still, Urs what do you think about my remark in the box ?
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeMar 24th 2011
I am not sure I follow the argument in the box. We should not distinguish between cohomology class and cocycle too much in the oo-context. But if you insist, you can say that the characteristic class is the image in the homotopy category of the characteristic map. In either case, what is characterized is a bundle.
-
- CommentRowNumber20.
- CommentAuthorzskoda
- CommentTimeMar 24th 2011
- (edited Mar 24th 2011)
I am saying there that historically it is not true that anybody named it because “it characterizes the cohomology theory” but because it is obtained using pullback along the characteristic map, the term which existed before. And as you say it characterizes a bundle. But this was also secondary. Primary is that the bundle is characterized a priori by a homotopy class of a map to the classifying space, thus characteristic map. It is only secondary that in some situations, the homotopy class of the map is determined already by what the pullback does at the cohomology level. But the homotopy level is primary and historically preceding. In any case, it is different from what you proposed for the explanation of the terminology (that it characterizes the cohomology theory).
We should not distinguish between cohomology class and cocycle too much in the oo-context.
I agree with this, but the map is not yet a cocycle, as it does not know which cohomology theory you consider it as a representative for (a class). So how is it characterizing cohomology, if you do not know which cohomology you are taking as a representative for ? It is just a map so far…
(I know that you prefer to choose derived hom in some model categoric situation what kind of makes it unique, but in topology indeed there are various things. Eventually all came from a universal one, but this is not behind the historical classes. They take values in certain, possibly generalized cohomology of spaces, H, evaluated at BG, it is possible that it has nontrivial coefficients. )
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeMar 25th 2011
I don’t know the history. It sounds strange to me that people would not call the cohomology class of a bundle a “characteristic” but only its classifying map. But if you say that’s how it was, you should edit the entry accordingly. Maybe give a reference.(I’d be interested in seeing this, too).
Concerning
the map is not yet a cocycle
No, the map is indeed the cocycle. A morphism in any -topos is precisely a degree-n cocycle in for cohomology on with coefficients in . If you wish to speak of “cohomology theories”: the cohomology theory in question is that presented by the Eilenberg-MacLane spectrum of .
-
- CommentRowNumber22.
- CommentAuthorjim_stasheff
- CommentTimeMar 25th 2011
I disagree strongly with some of the most recent posts:
I am saying there that historically it is not true that anybody named it because "it characterizes the cohomology theory"
It certainly was not meant to characterize the cohomology theory! in fact the language of cohomology theroy did not exist when charaactersitic classes were first introduced in 1935! see the preface to the book by Abel laureat Milnor and me.
but because it is obtained using pullback along the characteristic map,
That's a theorem - the original definitions were within the given bundle
We should not distinguish between cohomology class and cocycle too much in the oo-context.
Maybe in the oo-context but in general it's an important distinction: a map is not a homotopy class!
I agree with this, but the map is not yet a cocycle, as it does not know which cohomology theory you consider it as a representative for (a class). So how is it characterizing cohomology, if you do not know which cohomology you are taking as a representative for ? It is just a map so far...
21.Urs
13 hours ago
I don't know the history.
*Please get the history straight. for now, just fix the piece so no claim of historical accuracy is implied. -
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeMar 25th 2011
- (edited Mar 25th 2011)
just fix the piece
Could you please tell me what it is that needs to be fixed?
-
- CommentRowNumber24.
- CommentAuthorzskoda
- CommentTimeMar 25th 2011
- (edited Mar 25th 2011)
Well, Urs, I think the statement that the cohomology THEORY is intended to be characterized. This is what Jim and I are only and persistently complaining. Of course, Jim has additional historical points which I do not quite understand.
-
- CommentRowNumber25.
- CommentAuthorzskoda
- CommentTimeMar 25th 2011
- (edited Mar 25th 2011)
No, the map is indeed the cocycle.
Urs, didn’t I make it clear that I understand that. I am saying that it is not a cocycle in the sense that it is simultaneously cocycle in many cohomology theories, and to say that it is cocycle in some cohomology theory, you have to specify the theory.
I think nobody said that the class is not characteristic but only the underlying map/cocycle (I do not know where you find such statements in my text). Instead, historically the characteristic map (as well as its its homotopy class and possibly some cocycle descriptions, like differential forms) seems to be used widely earlier than the corresponding cohomology classes with their full cohomology interpretation, so it may be inaccurate to talk “cohomology” reason in explaining why word characteristic in that context.
Edit: On the other hand, I am not sure I fully understand Jim. It is also probably true (I do not know), that some particular characteristic classes were invented before they were called characteristic. Jim, you say that the original definition is whatever in terms of a bundle and only later a theorem has been proved that it is pullback. But I think only then the word characteristic was attached to the notion: not when the first examples of these classes were defined. Characteristic map first like characteristic function in set theory. It goes into a moduli space, into a classifying space of a sort. Characteristic functions distinguish object which are classified by the classifying space. I think that Urs was just referring to this phenomenon at cohomology level which was not primary historically, and used a bit awkward wording talking cohomology theory which just does not ring with my ear here.
Urs: now I do not know references off hand, but when you wrote your explanation first time I went into 1950s references and traced that the characteristic classes in them was very often related to the term characteristic maps which in this context I could trace to references in late 1940s, there were many. I think that in late 1930s mentioned by Jim, the words characteristic in this context were not yet use, but I may be wrong.
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeMar 25th 2011
- (edited Mar 25th 2011)
The entry does not say that a cohomology theory is being characterized. But that a cohomology class is being characterized. The cohomology class corresponds to a principal -bundle.
I have added a sentence on this.
-
- CommentRowNumber27.
- CommentAuthorzskoda
- CommentTimeMar 25th 2011
- (edited Mar 25th 2011)
I quote again what I quoted in 14:
This serves to characterize cohomology with coefficients in a complicated object A by a collection of cohomology classes with simpler coefficients. Therefore the name characteristic class .
Cohomology of a space with coefficients in something complicated is a way to get a cohomology theory. As coefficients vary in a general sense, the theories vary. Not ? Is there other reading of a “cohomology with complicated coefficients” than a cohomology theory ? It may be just the wording, but my reading, based on standard point of view, of this is that you said that the particular theory is reduced to knowing the classes. And that you claim that the word characteristic is from this. My understanding of the history of the word characteristic is what I said above.
-
- CommentRowNumber28.
- CommentAuthorzskoda
- CommentTimeMar 25th 2011
- (edited Mar 25th 2011)
Still the way the entry still reads
This serves to characterize cohomology with coefficients in a complicated object A by a collection of cohomology classes with simpler coefficients. Therefore the name characteristic class .
seems to differ from what I claim that the history of the term characteristic is. I mean you are saying that one can say characteristic class just when one means the whole collection of many characteristic classes simultaneously. Of course this makes sense, as to get the homotopy type (which determines the bundles) you need many invariants, and it is similarly true for the fixed cohomology theory. But the usage characteristic as I explained before seems to be used for a map and then for a single class, regardless the power of taking them all together at cohomological level. At the level of map there is one map so the power is truly there at the very beginning and is in the same spirit (so if the historical viewpoint would not be the objective of the philology I would not complain in the first place).
-
- CommentRowNumber29.
- CommentAuthorzskoda
- CommentTimeMar 28th 2011
- (edited Mar 28th 2011)
According to http://www-history.mcs.st-and.ac.uk/Biographies/Stiefel.html
was awarded his doctorate for his thesis Richtungsfelder und Fernparallelismus in n-dimensionalen Mannigfaltigkeiten from ETH Zürich in 1935. He published the results of this thesis in a paper in 1936.
the 1936., is of course Stifel’s paper on Stiefel-Whitney characteristic classes.
That sites quotes
- V Szebehely, D Saari, J Waldvogal, U Kirchgraber, Eduard L Stiefel (1909-1978), in Proceedings of the Sixth Conference on Mathematical Methods in Celestial Mechanics, Math. Forschungsinst., Oberwolfach, 1978, Celestial Mech. 21 (1) (1980), 3-4.
who say in the paper
… perhaps Stiefel’s most famous contribution to pure mathematics, was dedicated to a fundamental study of the theory of vector fields on manifolds. Generalising the classical notion of the Eulerian characteristic of a manifold, he introduced the idea of the characteristic classes.
This possibly (?) suggests that the “characteristic” was here mimicking word characteristic in “Euler characteristic”. Pretty disappointing understatement, I would say, comparing to the statement we all agree (characterizing vector bundles) has more interesting ramifications in its full power (specially at the level of homotopy classes, where the homotopy class of the map into the classifying space does it all).
Pontrjagin’s 1942 paper is
- Lev Pontrjagin, Characteristic cycles on manifolds, C. R. (Doklady) Acad. Sci. URSS (N.S.) 35, (1942). 34–37.
Eventually we will get some material for the future entry historical notes on characteristic classes featuring hopefully eventual correct explanation for the terminology.
Morita’s characteristic classes booklet is on the other hand, spending some time considering bundles not of vector spaces or spheres or disks but of surfaces (and sporadically higher dimensional manifolds), mainly of genus . Of course the gauge group is now infinite-dimensional, coefficients are in BDiff. Still he has the philosophy of the three cases of BDiff, BDIff-flat and the third term in the fiber sequence, just like in the usual case. Maybe Urs has more to say about this ?
-
- CommentRowNumber30.
- CommentAuthorzskoda
- CommentTimeMar 28th 2011
- (edited Mar 29th 2011)
So here I reproduce the entire Preface page from the book of Jim with Abel laureate Milnor :) I read the book some 16 years ago, in Fall 1995, so it wakes up good memories of this excellent text :)
The text which follows is based mostly on lectures at Princeton University in 1957. The senior author wishes to apologize for the delay publication.
The theory of characteristic classes began in the year 1935 with almost simultaneous work by HASSLER WHITNEY in the United States and EDUARD STIEFEL in Switzerland. Stiefel’s thesis, written under the direction of Heinz Hopf, introduced and studied certain “characteristic” homology classes determined by the tangent bundle of a smooth manifold. Whitney, then at Harvard University, treated the case of an arbitrary sphere bundle. Somewhat later he invented the language of cohomology theory, hence the concept of a characteristic cohomology class, and proved the basic product theorem.
In 1942 LEV PONTRJAGIN of Moscow University began to study the homology of Grassmann manifolds, using a cell subdivision due to Charles Ehresmann. This enabled him to construct important new characteristic classes. (Pontrjagin’s many contributions to mathematics are the more remarkable in that he is totally blind, having lost his eyesight in an accident at the age of fourteen.)
In 1946 SHING-SHEN CHERN, recently arrived at the Institute for Advanced Study from Kunming in southwestern China, defined classes for complex vector bundles. In fact he showed that the complex Grassmann manifolds have a cohomology structure which is much easier to understand than that of the real Grassmann manifolds. This has to a great clarification of the theory of real characteristic classes,We are happy to report that the four original creators of characteristic class theory all remain mathematically active: Whitney at the Institute Advanced Study in Princeton, Stiefel as director of the Institute for Applied Mathematics of the Federal Institute of Technology in Zurich, Pontrjagin as director of the Steklov Institute in Moscow, and Chern at the University of California in Berkeley. This book is dedicated to them.
JOHN MILNOR
JAMES STASHEFF
-
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeMar 28th 2011
- (edited Mar 28th 2011)
Zoran, I am not sure what to do, I am not sure what the disagreement is.
Why is the class of a map called a characteristic class of G-bundles?
Because it is a characteristic property of -bundles, no?
And the point is that is simpler than . Because a full characterization of a -bundle is by the map to . But by pushing that map further to the simpler abelian class, we learn something.
This is all that the entry means to say and which i think it does say. Is that really controversial? I don’t understand the discussion.
-
- CommentRowNumber32.
- CommentAuthorzskoda
- CommentTimeMar 28th 2011
- (edited Mar 28th 2011)
Urs, in the very first comment, in the query at the link, months ago, I said that the reasoning is CORRECT and BEAUTIFUL. Hence no disagreement about the mathematical content, now or never before. I said that UNFORTUNATELY, the history seem not to name “characteristic” for the reason you stated, related to “characterizing cohomology with coefficients in complicated objects”. Jim says there was no cohomology at the time. Stiefel link says that it was characteristic as it generalized Euler characteristic, disappointing if this was the main reason. I noted that in old time there was also the story about “characteristic” map, the terminology used less now. So in any case, if one takes at least one of the 3 remarks seriously, we can not say that the terminology “characteristic” came from “characterizing cohomology with coefficients in a complicated object” as it says in the entry. Whenever I say that you are reexplaining me mathematics which I understood when I gave the first comment. We are not talking mathematics, but the reason for the terminology, isn’t that clear ? It is strange that I do not succeed to communicate this simple issue to you. I think that in every remark of this thread I emphasised I am talking terminology and history and not mathematics (Edit: I have impression that not a single of my remarks was read word-by-word, that means I better not waste my time on arguing carefully in nForum in future and simply work on nLab without regard to consensus).
So I suggest retaining your reasoning but saying that the terminology historically came a bit different way and leave the task to clear the true history later in a separate entry historical note on characteristic classes.
Is that really controversial?
Yes, the statement that the name came about that way is (somewhat) controversial, and phrased as in the actual entry even more The people who named it probably did not know of Eilenberg-MacLane spaces either. The fact that reinvented history that way would be nice, logical and beautiful, I do agree (as it is correct, sound and beautiful mathematically!), and did agree from the start. This is called folk etymology: plausible and witty but not historically true. (A bit of it is true of course here, but it is an overstretch, or as it could be said, a hypercorrect version).
-
- CommentRowNumber33.
- CommentAuthorjim_stasheff
- CommentTimeMar 29th 2011
@zkoda: We are not talking mathematics, but the reason for the terminology, isn't that clear ? It is strange that I do not succeed to communicate this simple issue to you. I think that in every remark of this thread I emphasised I am talking terminology and history and not mathematics.
Zoran, You have my full support. Pseudo history is worse than no history. Meaning of words do evolve over time (especially quickly in physics!) but do not indulge in folk etymology - it presents false insights and obscures the true ones.
Thanks for inputting the preface from Minor and me - where do you guys find the time. Note! Stiefel worked in HOMOLOGY
not CO, as did Hopf when he invented what evolved into Hopf algebras. -
- CommentRowNumber34.
- CommentAuthorUrs
- CommentTimeMar 29th 2011
Jim,
I see you have strong feelings, but could you just tell me explicitly what you would want to be changed/added to the entry.
I don’t understand the discussion. I don’t know which “pseudo history” you are complaining about. Sorry. Just help me.
-
- CommentRowNumber35.
- CommentAuthorzskoda
- CommentTimeMar 29th 2011
- (edited Mar 29th 2011)
Thank you. I like of course very much what Urs is doing with explaining the motivations and reasoning from modern point of view he advances in and which eventually gives a clean and simpler picture; it is a natural problem with the time constraints that clearing up the various details, points of view and history is difficult (and the online discussions are energy consuming to all of us), without slowing down with writing, but eventually we will have things straight :)
Urs, I wrote few entries ago
So I suggest retaining your reasoning but saying that the terminology historically came a bit different way and leave the task to clear the true history later in a separate entry historical note on characteristic classes
Nobody has strong feelings here just the factual inaccuracy about history. I am going to change the entry now.
-
- CommentRowNumber36.
- CommentAuthorzskoda
- CommentTimeMar 29th 2011
- (edited Mar 29th 2011)
I replaced the incorrect
Therefore the name characteristic class.
by
Historically the name characteristic class came a little different way about, however.
This is safe until we take more time into tracing the history in a separate entry.
-
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeMar 29th 2011
Thanks, Zoran, for taking care of this. I let you and Jim sort this out.
One comment, though: I am a strong believer in the fact that there is progress in math and that we learn from history. If a concept was murky when first conceived and has meanwhile been clarified, I think it is bad to stick to the murky version in technical text just in order to reflect the history. When we write math, we are not writing a history book, but are trying to give a clear picture of reality.
-
- CommentRowNumber38.
- CommentAuthorzskoda
- CommentTimeMar 29th 2011
- (edited Mar 29th 2011)
I agree Urs, I said at the very beginning that the modern point of view should be followed, when explaining the concepts, but no intention to explain the WORDS should be done that way. Linguistics is also science. (Edit: I think it is not hard to separate motivation for math and etymology in written text; but also one can delegate more complicated bibliographies and alike to separate historical entries: I recently discussed with Toby about terminology for creating a cycle of history pages to have the main pages less heavy with historical material, while still the history recorded when somebody has the energy or knowledge to add bibliographies or other such data.)
I wrote stub for historical note on characteristic classes.
In
- E. Stiefel, RIchtungsfelder und Fernparallelismus in -dimensionalen Mannigfaltigkeiten, Comm. Math. Helv. 8 (1935)
page 324 (22 of “Separat” version), “Characteristik” (number) seems to appear for the first time
Die Zahl heisst due Characteristik des -Feldes auf der Sphaere .
I can scan the text for you if you like (I found it in Hirzebruch’s personal library).
-
- CommentRowNumber39.
- CommentAuthorzskoda
- CommentTimeMar 29th 2011
- (edited Mar 29th 2011)
OK pdf is free online
- Eduard Stiefel, Richtungsfelder und Fernparallelismus in -dimensionalen Mannigfaltigkeiten, Comm. Math. Helv. 8, 305-353 (1935-1936) perm URL
In later issue of this journal there is another article of Stiefel
- Eduard Stiefel, Über Richtungsfelder in den projektiven Räumen und einen Satz aus der reellen Algebra, Comm. Math. Helv. 13, 201-218 (1940-1941) perm URL
By the way, Max Planck Bonn has recently made a new web page and changed URLs for their preprints, what changes for lots of specific preprint links in Lab, I will take care of the principal ones, once I can. There is a conference in rep theory now in Bonn, I am not attending even that (except for Soergel’s talk on modular Koszul duality), being too busy. There was a talk on Rouquier-Khovanov-Lauda algebras but I did not attend it. fortunately I managed to attend Schwede’s excellent talk at MPI introducing the main steps in the construction of the category KMP (Kontsevich’s noncommutative motives) using non-connective K-theory spectra and dg-categories.
I have added (at characteristic class) the Morita reference mentioned in my question posed at the end of 29 of this thread.
-
- CommentRowNumber40.
- CommentAuthorDavid_Corfield
- CommentTimeSep 1st 2019
- (edited Sep 1st 2019)
I think this passage needs attention:
Generally,
is the cohomology of with coefficients in . Every cocycle represents a characteristic class on with coefficients in .
A -principal bundle is classified by some map . For any a degree cohomology class of the classifying space, the corresponding composite map represents a class . This is the corresponding characteristic class of the bundle.
There are different uses of , should stay as , and there’s no need to limit to , right?
So this could be
Generally,
is the cohomology of with coefficients in . Every cocycle represents a characteristic class on with coefficients in .
A -principal bundle is classified by some map . For any a degree cohomology class of the classifying space, the corresponding composite map represents a class . This is the corresponding characteristic class of the bundle.
-
- CommentRowNumber41.
- CommentAuthorDavid_Corfield
- CommentTimeSep 1st 2019
Or perhaps better to continue with instead of .
-
- CommentRowNumber42.
- CommentAuthorDavid_Corfield
- CommentTimeSep 1st 2019
1 to 42 of 42