nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorFinnLawler
- CommentTimeJan 23rd 2010
Created internal profunctor, which also describes an idea I saw somewhere about internal diagrams in fibrations over the base category. I added what I think are two examples, and asked a generic 'Help!' question. It might be better off on a page of its own, though.
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeJan 24th 2010
As I am currently at IP which id banned from updating the nlab, I will leave here a note, that the stuff which you saw "somewhere" is in the reference of Maclane and Pare from 1980s, JPAA. I planned to write something more about it, than it is written in their paper, but this has to wait for some time...
-
- CommentRowNumber3.
- CommentAuthorFinnLawler
- CommentTimeJan 27th 2010
Thanks for that, Zoran. I didn't mean to be coy about the reference -- it's just that the ones I've seen (not Mac Lane & Paré) weren't at all comprehensive. One was a page of the Elephant that Google Books let me see, the other was a brief mention in a 1979 Cahiers paper by Bunge and Paré, which refers to Paré & Schumacher in LNM 661. I should be able to get at that one, but not the JPAA paper, because the TCD library's subscription doesn't go back far enough.
-
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeJan 27th 2010
I should have a scan somewhere...I will find it for you, with few days of delay (remind me if nothing in a week).
-
- CommentRowNumber5.
- CommentAuthorFinnLawler
- CommentTimeJan 29th 2010
I expanded on Mike's remark at internal profunctor for the case of diagrams in a strict indexed category, but I can't quite figure it out for the pseudo case. Any suggestions?
-
- CommentRowNumber6.
- CommentAuthorMike Shulman
- CommentTimeJan 29th 2010
Maybe the Yoneda lemma for bicategories? I'm not sure exactly where you're stuck.
-
- CommentRowNumber7.
- CommentAuthorFinnLawler
- CommentTimeJan 29th 2010
- (edited Jan 29th 2010)
I should have explained the problem -- in the strict case you can treat both
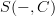 and
and 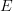 as internal categories in presheaves and apply Yoneda 'levelwise', as in the entry. I don't think this works if
as internal categories in presheaves and apply Yoneda 'levelwise', as in the entry. I don't think this works if 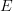 is only pseudo. Also, in that case the argument is not AFAICT a simple application of bicategorical Yoneda, because
is only pseudo. Also, in that case the argument is not AFAICT a simple application of bicategorical Yoneda, because 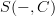 is not the hom-functor of a bicategory. In other words, the identity on
is not the hom-functor of a bicategory. In other words, the identity on  doesn't live in
doesn't live in 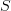 .
.You can still apply 1-categorical Yoneda and get
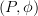 , but I don't see how to turn those back into a pseudonatural
, but I don't see how to turn those back into a pseudonatural 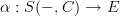 -- the inverse construction only gives you presheaves
-- the inverse construction only gives you presheaves 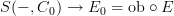 and ditto for arrows.
and ditto for arrows.It's late and my brain is a bit fried, so I'm probably missing something stupidly obvious. I'll try again after sleep.
-
- CommentRowNumber8.
- CommentAuthorMike Shulman
- CommentTimeJan 30th 2010
Ah. But you can treat S as a bicategory with trivial 2-cells, and
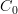 and
and 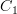 as objects of that bicategory, and then bicategorical Yoneda tells you that transformations
as objects of that bicategory, and then bicategorical Yoneda tells you that transformations 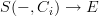 are the same as objects in
are the same as objects in 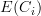 . The structure making the first one an indexed functor should be the same as the structure making the second an internal diagram.
. The structure making the first one an indexed functor should be the same as the structure making the second an internal diagram. -
- CommentRowNumber9.
- CommentAuthorzskoda
- CommentTimeFeb 2nd 2010
I still did not find the file for Saunders Maclane, Robert Paré, Coherence for bicategories and indexed categories* JPAA 1985 but will look this week at all file systems and backup CDs with my files.
-
- CommentRowNumber10.
- CommentAuthorzskoda
- CommentTimeFeb 2nd 2010
I have found it and sent a copy to F.L.
-
- CommentRowNumber11.
- CommentAuthorFinnLawler
- CommentTimeFeb 3rd 2010
@ Mike:
Thanks for your replies. I think I've got it now, though the only real difference is that
![[S^{op},\mathrm{Set}] [S^{op},\mathrm{Set}]](/extensions/vLaTeX/cache/latex_c52749420e432e8a16df9b1656f3f3fe.png) is embedded into
is embedded into ![[S^{op},\mathrm{Cat}] [S^{op},\mathrm{Cat}]](/extensions/vLaTeX/cache/latex_e49245da34784cb3d38ff5e351693465.png) . I may just have been overcomplicating things in my head before. However, it's possible that, being but a Bear of Very Little Brain, I've made a silly mistake, so a quick professional glance would be helpful.
. I may just have been overcomplicating things in my head before. However, it's possible that, being but a Bear of Very Little Brain, I've made a silly mistake, so a quick professional glance would be helpful.@ Zoran:
Thanks for that article! I'll give it a look and try to distil anything I find onto the lab.
-
- CommentRowNumber12.
- CommentAuthorncfavier
- CommentTimeMay 12th 2023
-
- CommentRowNumber13.
- CommentAuthorncfavier
- CommentTimeMay 12th 2023
Wait, a profunctor C ⇸ D is a bimodule D ⇸ C in Span? I am so confused.
-
- CommentRowNumber14.
- CommentAuthorvarkor
- CommentTimeMay 12th 2023
@ncfavier: as far as I’m aware, the standard convention on the nLab is that a profunctor is a functor .
-
- CommentRowNumber15.
- CommentAuthorncfavier
- CommentTimeMay 12th 2023
But that would correspond to a bimodule D ⇸ C, unless you mean to tell me that the left leg of a span represents “destination” and the right leg “source”…
It also doesn’t reflect the direction of the heteromorphisms, from D to C.
If this choice of notation is well-accepted and recognised, doesn’t it a minima deserve a huge red warning at the top of the relevant pages?
-
- CommentRowNumber16.
- CommentAuthorncfavier
- CommentTimeMay 12th 2023
I also don’t understand why this page claims that a bimodule C ⇸ 1 is equivalently a right C-module: the former has an underlying span C₀ → 1, while the latter has an underlying span C₀ → D₀, where D₀ is some set. So a right C-module is a functor , where D₀ is viewed as a discrete category.
Am I misunderstanding something?
-
- CommentRowNumber17.
- CommentAuthorBryceClarke
- CommentTimeMay 17th 2024
1 to 17 of 17