nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
expanded the discussion at equivariant homotopy theory
expanded the statement of the classical Elmendorf theorem
added the statement of the general Elmendorf theorem in general model categories
added remarks on G-equivariant oo-stacks, as special cases of this
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
just for empahsis of a point that I think should be relevant, I amplified now at the very beginning of the entry that the G-homotopies that define the G-homotopy category on the left side of Elmendorf's equivalence are of course precisely those induced by the interval/line object
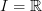 regarded as a G-space with trivial G-action.
regarded as a G-space with trivial G-action. -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJan 28th 2010
just for emphasis, even though it may be a very obvious thing to say, I indluded a section that says how the homotopical category of G-spaces as usually considered is refined to a Kan-complex enriched category with hom-SSet
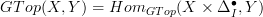 ,
,where
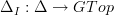 is the cosimplicial object induced from the geometric interval
is the cosimplicial object induced from the geometric interval 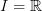 with trivial G-action.
with trivial G-action.Even though a very obvious thing to say, this (oo,1)-perspective now suggests that we stabilize this (oo,1)-category at the geometric loopings by
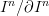 .
. -
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeJan 28th 2010
It would be nice to extend the treatment of G-equivariant homotopy theory to closely related orbispace homotopy theory.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeJan 29th 2010
- (edited Jan 29th 2010)
put in the Morel-Voevodsky discussion of how the equivariant homotopy category is the homotopy category of oo-sheaves on G Top localized at the interval object
(oo,1)-cat of G-equivariant spaces.
I think I got this right, but check with the given reference.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeAug 12th 2015
- (edited Aug 12th 2015)
have added a pointer to
- Mike Shulman, Univalence for inverse EI diagrams (arXiv:1508.02410)
-
- CommentRowNumber7.
- CommentAuthorDavid_Corfield
- CommentTimeAug 12th 2015
I was wondering if there was a connection to Charles Rezk’s global equivariant cohesion. Now I see you added a reference to Mike’s paper at global equivariant homotopy theory. Do you see a connection?
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeAug 12th 2015
- (edited Aug 12th 2015)
-
- CommentRowNumber9.
- CommentAuthorDavid_Corfield
- CommentTimeAug 12th 2015
But there’s no sign of cohesion appearing in Mike’s paper, is there?
-
- CommentRowNumber10.
- CommentAuthorUrs
- CommentTimeAug 12th 2015
Here I am not sure what your “but” refers to.
Regarding cohesion, Mike has a note in preparation with a comprehensive account of cohesive HoTT. Combing that with what seems (unless I am mixed up) a consequence of his present preprint should say that Charles’ sliced version of the equivariant cohesion is a model for cohesive HoTT with strict univalent universes.
-
- CommentRowNumber11.
- CommentAuthorDavid_Corfield
- CommentTimeAug 12th 2015
I just meant, from my cursory glance, it didn’t seem to me that Mike’s paper was motivated by anything to do with cohesion.
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeAug 12th 2015
- (edited Aug 12th 2015)
Right it isn’t, but I don’t see what you mean to imply by saying so.
What Charles Rezk discusses in 5.2, 5.3 is an -topos that he writes . What I said in #8 is that is an EI--category. And I was guessing that that finiteness condition holds here, too. If so, then by Mike’s preprint would be a model of HoTT with univalent strict universes. Unless I am missing something.
Now it is true that on top of that Charles has the nice statement that is cohesive over . The latter is also presheaves over an EI--category, that’s the example that Mike makes explicit in his preprint.
Put together, these two statements would seem to imply that this gives a model for cohesive HoTT with univalent strict universes.
-
- CommentRowNumber13.
- CommentAuthorMike Shulman
- CommentTimeAug 12th 2015
Can you explain why is an inverse EI--category?
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeAug 12th 2015
Yeah, I am wrong, it’s not. Sorry for the distraction.
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeJan 12th 2016
- (edited Jan 12th 2016)
In the Idea-section both at equivariant homotopy theory and at topological G-spaces I have added a paragraph that makes more explicit where the fixed-point wise homotopy equivalences come from
The canonical homomorphisms of topological -spaces are -equivariant continuous functions, and the canonical choice of homotopies between these are -equivariant continuous homotopies (for trivial -action on the interval). A -equivariant version of the Whitehead theorem says that on G-CW complexes these -equivariant homotopy equivalences are equivalently those maps that induce weak homotopy equivalences on all fixed point spaces for all subgroups of (compact subgroups, if is allowed to be a Lie group). By Elmendorf’s theorem, this, in turn, is equivalent to the (∞,1)-presheaves over the orbit category of . See below at In topological spaces – Homotopy theory.
-
- CommentRowNumber16.
- CommentAuthorDavid_Corfield
- CommentTimeJan 12th 2016
That’s the clearest description I’ve seen of the naive/genuine distinction. Is the difference expressible in HoTT in terms of working in the context , dependent sum/product for co(invariants), etc.? Perhaps the genuine version is more simply expressed?
-
- CommentRowNumber17.
- CommentAuthorDavid_Corfield
- CommentTimeJan 12th 2016
Maybe you’re warning against this here
For G a discrete group (geometrically discrete) the homotopy theory of G-spaces which enters Elmendorf’s theorem is different (finer) than the standard homotopy theory of G-∞-actions, which is presented by the Borel model structure
But then what allows the expression of the finer aspects? Something geometric? Cohesive, at least?
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeJan 12th 2016
re #16: sorry, I didn’t put that well after all.
I had been prompted by the paragraphs in Goodwillie 03, p.5, 6 (of 67) but maybe some care is due here. In any case, I have rephrased a bit more, just to bring out the “G-Whitehead theorem” better, which says that those fixed-point wise weak homotopy equivalences are, on G-CW-complexes, the evident G-equivariant homotopy equivalences.
-
- CommentRowNumber19.
- CommentAuthorDavid_Corfield
- CommentTimeJan 12th 2016
- (edited Jan 12th 2016)
Well anyway, it would interest me to see how renderings in HoTT allow expression in something closer to natural language, as Mike does in Univalence for inverse EI diagrams, example 7.5:
from a propositions-as-types point of view, we might say that A consists of a type with a G-action together with, for each fixed point of this action, a type of “special reasons” why that point should be considered fixed (which might be empty). That is, in passing from (the naive homotopy theory of) G-spaces to -diagrams, we make “being a fixed point” from a property into data.
Is ’naive’ being used in the sense as opposed to ’genuine’ here? So then, especially with a with many subgroups, the expression of the genuine would be rather complicated. Is there a reason why we need to range over all subgroups?
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeJan 12th 2016
- (edited Jan 12th 2016)
That quote gives natural language for speaking about the homotopy theory that is presented by the orbit category. But I would think that what you were after is something like an intrinsic internal characterization of this homotopy theory.
The following vague thought had occured to me:
if we consider global equiviance not under Lie groups but under finite groups, then the global orbit category is just the -category of homotopy 1-types with finite . If we did this for “2-equivariance” as in “2-equivariant elliptic cohomology” then we’d be looking at 2-groupoids with finite homotopy groups. Generally then we could consider the -category of homotopy types with finite homotopy groups as a site for “global -equivariance”.
This reminds us of the (opposite) of finite homotopy types, which is the site for the classifying topos for an object. As we are discussing elsewhere, this is the origin of Goodwillie calculus.
Now, of course, despite the similarity in name, finite homotopy types are different, in fact pretty much complementary to, homotopy types with finite homotopy groups. So maybe we’d want to combine them, somehow, to merge Goodwillie theory with global equivariant homotopy theory. And maybe the -category which suitably subsumes both finite homotopy types and homotopy types with finite homotopy groups is the site for a good classifying -topos, i.e. maybe that -topos has a good internal characterization.
Just speculating.
-
- CommentRowNumber21.
- CommentAuthorDavid_Corfield
- CommentTimeJan 12th 2016
Sounds interesting. What already exists as equivariant Goodwillie theory? I see there is
- Emanuele Dotto, Higher Equivariant Excision, arXiv:1507.01909
which refers to another couple of his own papers.
-
- CommentRowNumber22.
- CommentAuthorMike Shulman
- CommentTimeJan 12th 2016
BTW, this is different from the naive/genuine distinction for -spectra; that’s a further bifurcation within the world of fixed-point-wise equivariant homotopy theory. So perhaps “naive” is a poor choice of word here…
Note that there’s actually a whole range of possible “-equivariant homotopy theories” parametrized by a family of subgroups of ; the “most naive” one corresponds to choosing only the trivial subgroup.
-
- CommentRowNumber23.
- CommentAuthorDavid_Corfield
- CommentTimeJan 12th 2016
Re #20, what if anything stands in the way of global equivariance for all homotopy types with finite homotopy groups? I see Charles Rezk thought things should work out with 2-groups here.
Is there a suitable sense of compactness for Lie n-groups?
-
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeApr 12th 2018
Made explicit the pointer to the equivariant Whitehead theorem (notably in the statement of this theorem)
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeApr 12th 2018
-
- CommentRowNumber26.
- CommentAuthorTim_Porter
- CommentTimeJul 5th 2018
-
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeMar 11th 2019
added pointer to today’s
- Mehmet Akif Erdal, Aslı Güçlükan İlhan, A model structure via orbit spaces for equivariant homotopy (arXiv:1903.03152)
(just for completeness)
-
- CommentRowNumber28.
- CommentAuthorUrs
- CommentTimeDec 22nd 2021
added pointer to:
- Bert Guillou, Equivariant Homotopy and Cohomology, lecture notes, 2020 (pdf)
-
- CommentRowNumber29.
- CommentAuthornilesjohnson
- CommentTimeNov 16th 2022
I’ve updated this Hill, Hopkins, Ravenel reference to point to their 2021 book, since it’s a more thorough treatment of the material. As far as I can tell, nothing on the page points directly to the previously listed article, but I can put the article back anyway if someone wishes.
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeNov 17th 2022
Thanks!
I have re-instantiated (here) the cross-link with Arf-Kervaire invariant problem, assuming that you deleted it by accident.
-
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeNov 17th 2022
- (edited Nov 17th 2022)
[ mysterious duplicate removed ]
-
- CommentRowNumber32.
- CommentAuthornilesjohnson
- CommentTimeNov 17th 2022
re #30: ugh, yes; thanks!
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeJun 17th 2024
added pointer to:
- Graeme Segal, Some results in equivariant homotopy theory (1978) [scan: web, pdf]
This document seems to have existed only as a scan hosted as 6 separate html pages at homepages.warwick.ac.uk/~maaac/segal.html, /segal2.html, /segal3.html, /segal4.html, /segal5.html, /segal6.html.
I have merged these six html pages into a single pdf file (here). The result has overly large margins and bad page breaks, but otherwise is readable.
1 to 33 of 33