nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 4th 2010
- (edited Feb 4th 2010)
I added to covering space a section In terms of homotopy fibers that explains the universal covering space as the homotopy fiber/principal oo-bundle classified by the cocycle that is the constant path inclusion
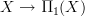 of topological groupoids.
of topological groupoids.To fit this into the entry, I added some new sections and restructured slightly. Todd and David should please have a look.
What I just added is essentially what David Roberts says in various query boxes, notably in what is currently the last query box. Back then we talked about the "Roberts-Schreiber construction" or whatnot, but really what this is is just the standard way to compute homotopy fibers in the oo-category of oo-groupoids.
I suspect that Todd's bar construction described there can similarly be understood as being nothing but another way to compute the more abstractly defined homotopy pullback in concrete terms. I'll have to think about this, though. But probably Tim Porter or Mike Shulman will immediately recognize this as the relevant bar construction of homotopy pullbacks in homotopy coherent category theory.
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeFeb 4th 2010
- (edited Feb 4th 2010)
Isn't there a way to realize a covering space as a sheaf (of sets) on the open sets of a topological space? -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeFeb 4th 2010
Yes, the sheaf of its sections. As we just discussed in the other thread: the stack of covering spaces is the stackification of the one constant on
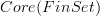 . A section of this is a locally constant sheaf, the locally constant sheaf of sections of the covering space.
. A section of this is a locally constant sheaf, the locally constant sheaf of sections of the covering space.I am about to add more on this to the Lab. But currently I can't quite decide where it should go!
-
- CommentRowNumber4.
- CommentAuthorHarry Gindi
- CommentTimeFeb 4th 2010
So does that mean that the category of covering spaces is the category of etale bundles (as in Mac Lane and Moerdijk's sense)? If this is true, does the unversal cover have a nice definition as a sheaf like the initial or terminal object? I only ask this because the category of sheaves is a topos. -
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeFeb 4th 2010
So does that mean that the category of covering spaces is the category of etale bundles (as in Mac Lane and Moerdijk's sense)?
Etale spaces are more general. Every sheaf (on a topological space) X is the sheaf of sections of some etale space over X. Locally constant sheaves are those that are sections of covering spaces.
I am about to add more on this to the Lab. But currently I can't quite decide where it should go!
I started now locally constant sheaf and constant sheaf
-
- CommentRowNumber6.
- CommentAuthorHarry Gindi
- CommentTimeFeb 4th 2010
One last question: If we remove the connectedness assumptions on covering spaces, do we recover the whole category of etale spaces? -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeFeb 4th 2010
I think what makes finite covering spaces special etale spaces is that they have a more restrictive condition on what thy look like locally: they need to be what is called evenly covering instead of just being local homeomorphisms.
-
- CommentRowNumber8.
- CommentAuthorHarry Gindi
- CommentTimeFeb 4th 2010
I must be wrong, but it seems to me like local homeo <=> evenly covering. Where am I going wrong? -
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeFeb 4th 2010
- (edited Feb 4th 2010)
there is a remark on this at etale space, which I now also copied over to covering space:
Every covering space (even in the more general sense not requiring any connectedness axiom) is an etale space but not vice versa: for a covering space the inverse image of some open set in the base B needs to be, by the definition, a disjoint union of homeomorphic open sets in E; however the ‘size’ of the neighborhoods over various e in the same stalk required in the definition of étalé space may differ, hence the intersection of their projections does not need to be an open set.
Possibly there is room to say this in a bit more detail.
-
- CommentRowNumber10.
- CommentAuthorHarry Gindi
- CommentTimeFeb 4th 2010
- (edited Feb 4th 2010)
Ah, thanks a lot. -
- CommentRowNumber11.
- CommentAuthorzskoda
- CommentTimeFeb 4th 2010
Oh, I am now happy that I wrote that remark at etale space some time ago :)
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeFeb 4th 2010
Yes very good!
But maybe we could add a comment about finiteness, then: what if we have etale spaces with finite stalks. How different can they be from covering spaces? I guess now Harry's original idea comes into play: in that case it is only connectedness that distinguishes covering spaces from general finite etale spaces. I guess.
-
- CommentRowNumber13.
- CommentAuthorzskoda
- CommentTimeFeb 4th 2010
- (edited Feb 4th 2010)
Well intersection of finitely many opens downstairs is open.
Connectedness is not always asked for in covering spaces. This is more special definition in the theory, in order to relate it to Galois theory/fundamental group. Spanier has for example no restrictions in the very definition of covering space. If one wants to have the connection to the fundamental group, then and deck transformations one needs more conditions, including that the base space is linearly connected and locally linearly connected and that the covering space is connected as well. We should treat all these levels of generality, including the definition of a regular covering. In general I like the approach in Spanier (which I reviewed just few weeks ago).
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeFeb 4th 2010
Well intersection of finitely many opens downstairs is open.
Yes, so that's why I am saying with finite fibers, etale spaces and covering spaces must be pretty much the same
-
- CommentRowNumber15.
- CommentAuthorDavidRoberts
- CommentTimeFeb 5th 2010
@Urs
The problem with general etale spaces is that they are not locally trivial - for example, take an open cover X (or even just some open sets, not necessarily a cover) form the disjoint union with its canonical map to X. This map is etale (a local homeomorphism) but nowhere like a covering space. If this collection of open sets is point finite, then we have an etale space with finite fibres...
If the etale space is connected, however, I'm still not sure that this is enough. I think (but please check) that the projection from the (non-Hausdorff) space that is the real line with 0 doubled to the real line is etale with finite fibres, but it is not a covering projection. -
- CommentRowNumber16.
- CommentAuthorTobyBartels
- CommentTimeFeb 5th 2010
I'll agree that that map's étale, but the obvious question is: What about a connected Hausdorff étalé space with finite fibres?
-
- CommentRowNumber17.
- CommentAuthorHarry Gindi
- CommentTimeFeb 5th 2010
Question: Might it not be better to call it espace étalé on nLab?? It just rolls off the tongue, while étalé space just sounds bad no matter how you say it. -
- CommentRowNumber18.
- CommentAuthorDavidRoberts
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
@Toby
Hmmmm. Maybe there's a counterexample using a non-semilocally 1-connected base? -
- CommentRowNumber19.
- CommentAuthorDavidRoberts
- CommentTimeFeb 5th 2010
@Harry
Well technically it is the map that is etale, in that it is a local homeomorphism/diffeomorphism/biholomorphism/etc. Espace etale has a particular meaning also - there was some discussion on this, possibly from Zoran. -
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeFeb 5th 2010
Thanks David, of course. I added that remark to etale space and covering space.
(Let me all remind you: it is forbidden to say anything useful here without making sure a copy of it survives on the nLab, in some form! :-))
-
- CommentRowNumber21.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
Urs: As far as surviving, I have the feeling that many good things from café which appeared after the nlab did not get into nlab. I am not complaining as all of us are too busy, but suggesting what I did before, I mean if somebody can suggest to Jacques or somebody, if it is not too hard, to get "source" button for indvidual posts at café available. Namely, some discussions, especially those most technical, hence frequently most valuable ones, have lots of formulas. In answering to those posts, inquoting them in nlab, and finally for pedagogical purpose of learning the script, it woudl be very useful to be able to see the source code of chosen individual comment or post in cafe. If the source code is preserved at all (I do not know how it works there, as I am not insider or author there).
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeFeb 5th 2010
Right, so as I may have said before: drop me a note when you want source code to be copied. I can access it.
-
- CommentRowNumber23.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
That may be a solution for me, and I remember your kind offer, but still if there is any lite effort in improving the cafe system in sight, this issue is my preferred choice :)
-
- CommentRowNumber24.
- CommentAuthorTobyBartels
- CommentTimeFeb 5th 2010
@ Zoran
It is preserved. If the poster PGP-signs their work, then you can even view it.
-
- CommentRowNumber25.
- CommentAuthorHarry Gindi
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
@DavidRoberts Unless I'm reading what you wrote incorrectly, you're mistaken.
We're talking about espace etale, which is the "spreading out" of the sheaf data.
Etale maps are something _completely_ unrelated. An etale map is a map of commutative rings so that if S an R-algebra and the map R->S is etale, given T any R-algebra and J any ideal such that J^2=0, then given any map S->T/J such that the map R->T/J factors into R->S->T/J, then there exists a unique map S->T such that R->T factors into R->S->T. There's a much nicer way to say this using modules of kahler differentials, but I don't remember the formulation. These maps translate into maps in Aff=CRing^op, but I don't remember what the condition is for a general scheme. Probably something like the scheme can be covered by affine schemes whose inclusion maps are etale. \'etale (this case) means something like "calm (water in the ocean)", which emphasizes that the map is both smooth and unramified. The other word, \'etal\'e means "spread out", like I said.
Anyway, this is completely unrelated to espace etale.
You've confused the two precisely backwards =)! -
- CommentRowNumber26.
- CommentAuthorDavidRoberts
- CommentTimeFeb 5th 2010
Hmm ok. Then where did 'espace (=space) etale' come from? Does a map that is etale in CRing give rise to a map in Aff that is a local isomorphism (assuming say we get smooth complex varieties or something out)? -
- CommentRowNumber27.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
Espace etale or etale space is the one which by definition corresponds to etale map in continuous world. In algebraic geometry, a morphism is etale if it is smooth of relative dimension 0. Equivalently flat and unramified, or smooth and unramified. So in the category of schemes and flat morphisms of schemes. Thus etale morphisms (word used in algebraic geometry) is a precise analogue of the notion of etale map from usual topological setup. Harry, why do you object ? See etale morphism entry distinct from etale map entry (I think that I initially wrote both entries).
-
- CommentRowNumber28.
- CommentAuthorHarry Gindi
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
An etale ring map is precisely what I described. An etale morphism is the corresponding map in the category of schemes.
The projection map of an espace etale onto its base space is just called the bundle or the projection map. They are totally and entirely unrelated.
The "fonction \'etale", that you noted in your article makes precisely the same mistake. In fact, it's "calm" because it's smooth and unramified. That is, it's "a better type of map than a smooth map". If it were in complex algebraic geometry, these maps would be just like you said on that page. -
- CommentRowNumber29.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
You described for rings in some detail the infinitesimal lifting property for formally smooth morphisms. I do not distinguish rings and affine schemes in terminology, and this is not an issue.
The projection of an etale space is etale map in topological category. Period.
Etale means local homeomorphism there, the terminology being standard.
This is totally parallel to the situations in smooth category and in the category of algebraic schemes.
So far I do not get which mistake you alude ? So far it looks to me a strange claim.
-
- CommentRowNumber30.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
To add, espace etale is just the total space of etale map in topology, by definition. I am not sure if you object the variant of the standard terminology or the sufficiently formal semantic parallelism in algebraic, differential and topological category ?
-
- CommentRowNumber31.
- CommentAuthorHarry Gindi
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
What do you mean an etale map in the category of topological spaces? That doesn't mean anything to me. Do we have a notion of etale for an arbitrary category? The two notions are completely unrelated as far as I can tell. -
- CommentRowNumber32.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
No, we don't. We have the definitions of etale maps in at least 4 contexts, which appear to be the category of topological spaces and continuous maps, category of schemes (or analytic spaces) and smooth morphisms of schemes (or of analytic spaces) and category of smooth manifolds and smooth morphisms. The category of affine schemes is just a subcategory of all schemes, hence your special case. A smooth map of schemes is etale iff there is a cover of the total scheme by Zariski-open subschemes which project by an isomorphism of schemes onto open subschemes of the base. In particular it induces the topological etale maps of the underlying topological spaces, but local isomorphism includes the sheaf pat as well.
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeFeb 5th 2010
A smooth map of schemes is etale iff there is a cover of the total scheme by Zariski-open subschemes which project by an isomorphism of schemes onto open subschemes of the base. In particular it induces the topological etale maps of the underlying topological spaces, but local isomorphism includes the sheaf pat as well.
This should be added to etale morphism.
-
- CommentRowNumber34.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
We could take a cover U of the scheme/space E above and a cover V of the scheme/space M below, and an isomorphism iso : U to V forming a commutative square U to E to M equals U to V to M. This characterizes etale maps in all 4 categories mentioned, equipped with corresponding topologies (Zariski, not etale in the case of schemes).
-
- CommentRowNumber35.
- CommentAuthorHarry Gindi
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
Alright, I think I've got it. There's a characterization of etale extensions that they're locally standard etale at every prime. Then we can represent S as a product of standard etale extensions of (something). When we pull our dual stuff, this gives an epimorphism from the coproduct of the spectra of all of the standard etale extensions, which gives us the analog of a covering-space type of map?
Okay, I think I have the idea then. Isn't there a category theoretic term for a surjection from the coproduct where each component is an injection? (replace surjection and injection with the correct strengths of epics and monics.) -
- CommentRowNumber36.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
I entered the claim suggested by Urs.
For Harry: I don't know, now we are getting to terminological issue closer to Toby's expertise.
By the way, Michael Artin has written a fairly long paper in 1994 where one of the main issues is the study of etale morphisms of noncommutative rings. This is unpublished (I have the file somewhere). There are alterantive approaches nowdays, but Misha's treatment is elementary and very concrete, I liked it (it was long since i looked at it, and forgot it, but remember the feeling).
-
- CommentRowNumber37.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
Wait, sorry, something is wrong in one of my newest claims above, namely it is OK but it should be in etale topology, not Zariski (this makes it circular for the definition, but appropriately consistent with the picture); Zariski opens are too big for this to work in any example. The disjointness is exactly the thing which is achieved by etale covers (this is very essential and makes it really parallel to classical situation).
-
- CommentRowNumber38.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
On the other hand, passage from the condition from affine schemes to the general case is not difficult. For example the relative dimension is defined in each fiber and formal smoothness is clearly Zariski local.
-
- CommentRowNumber39.
- CommentAuthorDavidRoberts
- CommentTimeFeb 5th 2010
The term local isomorphism captures 'local homeomorphism' well for any category, and the latter has been used for the maps in question in many places (I only use etale because it is shorter than local homeomorphism, and not specific to Top). But then we need to know what 'local' means - for schemes local is in terms of the opposite of maps called 'etale' in CRing, but as Zoran points out these can be characterised in other ways. For spaces, open covers suffice. -
- CommentRowNumber40.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
- (edited Feb 5th 2010)
Smooth morphisms of schemes are finitely presented so the difference between covering maps and etale maps in topology does not play a role here. This makes it easier to see that taking pullbacks of etale morphism by appropriate etale cover leads to morphism which is etale at the level of locally ringed spaces (unlike the original map which is not).
Edit: when one mentions locally ringed space it must be Zariski, etale makes no sense as usual topology here. But etale cover makes the situation at the pullback disjoint enough that by then the usual topology suffices.
-
- CommentRowNumber41.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
for schemes local is in terms of the opposite of maps called 'etale' in CRing
Right David, but not only that etale are used to define the locality needed here, the etale morphisms in CRing are themselves (opposite to) etale maps of corresponding affine schemes.
-
- CommentRowNumber42.
- CommentAuthorTobyBartels
- CommentTimeFeb 5th 2010
Zoran (#32) refers above to etale map as distinct from etale morphism, but the former does not actually exist. (Possibly Zoran was thinking of etale space, where the term is mentioned.) So I started it, with a note that as to how it appears in Zoran's four examples.
-
- CommentRowNumber43.
- CommentAuthorHarry Gindi
- CommentTimeFeb 5th 2010
Please don't do it! The proper terminology is "a universally strict epimorphism". It makes sense on any site with coproducts. -
- CommentRowNumber44.
- CommentAuthorDavidRoberts
- CommentTimeFeb 5th 2010
Does a universally strict epimorphism have anything to do with a strict epimorphism? The latter makes sense in any category whatsoever.
-
- CommentRowNumber45.
- CommentAuthorzskoda
- CommentTimeFeb 5th 2010
Right Toby, the entry etale map from my memory is actually the entry etale space.
-
- CommentRowNumber46.
- CommentAuthorHarry Gindi
- CommentTimeFeb 5th 2010
- (edited Feb 7th 2010)
redacted -
- CommentRowNumber47.
- CommentAuthorDavidRoberts
- CommentTimeFeb 7th 2010
- (edited Feb 7th 2010)
Sorry, Harry, I'm not sure what your response is to.
Edit: As for strict epimorphisms, I just searched and found that they are defined in Grothendieck's Seminaire Bourbaki No 190 (definition 2.2) - collected in FGA. I should add this to the page strict epimorphism for reference.
-
- CommentRowNumber48.
- CommentAuthorHarry Gindi
- CommentTimeFeb 7th 2010
Never mind. Sorry. -
- CommentRowNumber49.
- CommentAuthorUrs
- CommentTimeJan 24th 2017
I have streamlined the statement of the “fundamental theorem” at covering space a little.
Eventually I’ll want this page to be ready for public consumption, usable as lecture notes. Presently it’s a bit of a mess. There are a handful of ancient query box comments sitting there, various from David (Roberts), some from Todd. Eventually I will be wishing to and working on removing these such as to make the entry text be finalized and polished.
-
- CommentRowNumber50.
- CommentAuthorDavidRoberts
- CommentTimeJan 25th 2017
Anything that I wrote there can be removed. If I get the urge to think about such topics again I can go back to the history of the page.
-
- CommentRowNumber51.
- CommentAuthorUrs
- CommentTimeJul 1st 2017
I have added the statement and the detailed elementary proof of the path lifting property of covering spaces: here.
-
- CommentRowNumber52.
- CommentAuthorUrs
- CommentTimeJul 1st 2017
- (edited Jul 1st 2017)
I have also added statement and proof of “the lifting theorem” for covering spaces (here)
Presently the very last step in the proof is hard to read. I’ll see if I can improve this tomorrow.
-
- CommentRowNumber53.
- CommentAuthorUrs
- CommentTimeJul 2nd 2017
Okay, I have improved (I hope) the phrasing of the last bit of the proof of “the lifting theorem” (in the section Properties – Lifting properties). In the course I added some further basics, such as the statement and proof that a covering projection is an open map (in the section Properties – Basic properties).
-
- CommentRowNumber54.
- CommentAuthorUrs
- CommentTimeJul 2nd 2017
I have splitt off an entry
from the entry covering space and moved to it Todd’s category-theoretic discussion In terms of a coend. Then I added also a description of the elementary construction.
(I am working towards a detailed expositional discussion of the fundamental theorem of covering spaces and am finding it helpful to organize the material a bit more, for readability. There is still other stuff at covering space that might usefully be moved to elsewhere.)
-
- CommentRowNumber55.
- CommentAuthorTodd_Trimble
- CommentTimeJul 2nd 2017
I noticed. I would probably like to weigh in at some point on organizational matters, but I’m glad you’re thinking about this. One thing I might mention is that the whole “monodromy” discussion provides an explicit adjoint equivalence and obviates any need to bring up the axiom of choice (or at least this aspect should be brought out better), i.e., the fundamental theorem of covering space theory should make this adjoint equivalence explicit and hopefully not just say a certain functor is essentially surjective and fully faithful.
-
- CommentRowNumber56.
- CommentAuthorUrs
- CommentTimeJul 2nd 2017
- (edited Jul 2nd 2017)
Thanks, Todd, for some patience. I might be about to change my mind and move it all back. But in either case the entry deserves some tidying-up.
I have tried to spell out the proof of the “fundamental theorem” now here.
It’s all very tautological, of course, but so I need to beware not falling into traps. For instance, I seem to think that the assumption on the base space needed is, besides semi-local simply-connectedness, that it be locally path-connected. Elsewhere I see instead local connectedness assumed. (?)
-
- CommentRowNumber57.
- CommentAuthorTodd_Trimble
- CommentTimeJul 2nd 2017
It’s totally fine, Urs. I agree that the article was in need of tidying up, and please take your time.
It may be tautological, but this is the sort of “trivially trivial” material that category theory is good at rendering, and besides it’s hard to get the kind of quality of exposition in textbooks that I think we are ultimately after here. (Most textbooks still futz around with basepoints and stick to groups, not groupoids. It should be done right after all.)
-
- CommentRowNumber58.
- CommentAuthorDavidRoberts
- CommentTimeJul 3rd 2017
the assumption on the base space needed is, semi-local simply-connectedness, that it be locally path-connected
Correct.
-
- CommentRowNumber59.
- CommentAuthorUrs
- CommentTimeJul 10th 2017
- (edited Jul 10th 2017)
-
- CommentRowNumber60.
- CommentAuthorUrs
- CommentTimeJul 10th 2017
For completeness I have
split off an entry groupoid representation from representation
created an entry category of covering spaces.
-
- CommentRowNumber61.
- CommentAuthorUrs
- CommentTimeJul 17th 2017
I have been editing the section Lifting properties.
Now the homotopy lifting property is stated in the generality that deserves this name (here) and the corollary “lift of homotopy between paths relative starting point for given lift of paths” is now an example afterwards (here).
-
- CommentRowNumber62.
- CommentAuthorUrs
- CommentTimeJul 18th 2017
- (edited Jul 18th 2017)
after the homotopy lifting lemma for covering spaces, I added a remark here saying that
this means that covering spaces are Serre fibrations,
there are counterexamples to them being always Hurewicz fibrations,
but the latter holds if base and total space admit CW-structure.
-
- CommentRowNumber63.
- CommentAuthorUrs
- CommentTimeJul 19th 2017
Hm, now I got myself mixed up. In the proof of the homotopy lifting lemma for covering spaces here, does it really need local (path-)connectedness?
-
- CommentRowNumber64.
- CommentAuthorUrs
- CommentTimeJul 19th 2017
Ah, that counterexample (here) is for “generalized covering spaces”.
-
- CommentRowNumber65.
- CommentAuthorUrs
- CommentTimeJul 19th 2017
- (edited Jul 19th 2017)
Okay, so I have added to Hurewicz fibration a mentioning of covering spaces as examples here.
-
- CommentRowNumber66.
- CommentAuthorUrs
- CommentTimeDec 25th 2021
added pointer to:
- William S. Massey, Chapter 5 of: Algebraic Topology: An Introduction, Harcourt Brace & World 1967, reprinted in: Graduate Texts in Mathematics, Springer 1977 (ISBN:978-0-387-90271-5)
-
- CommentRowNumber67.
- CommentAuthorUrs
- CommentTimeJun 25th 2022
- (edited Jun 25th 2022)
added these pointers:
Discussion of (homotopy types of) covering spaces via homotopy type theory:
Kuen-Bang Hou, Covering Spaces in Homotopy Type Theory, extended abstract Type Theory, Homotopy Theory and Univalent Foundations (2013) doi:10.1007/978-3-319-21284-5_15
Kuen-Bang Hou, Robert Harper, Covering Spaces in Homotopy Type Theory, Leibniz International Proceedings in Informatics (LIPIcs) 97 (2018) doi:10.4230/LIPIcs.TYPES.2016.11, pdf
and with emphasis on the -truncation-modal homotopy type theory involved:
- Felix Cherubini, Egbert Rijke, Def. 8.5 of: Modal Descent, Mathematical Structures in Computer Science 31 4 (2020) arXiv:2003.09713, doi:10.1017/S0960129520000201
-
- CommentRowNumber68.
- CommentAuthorDmitri Pavlov
- CommentTimeNov 17th 2023
Added:
A detailed treatment is available in
- Nicolas Bourbaki, Topologie Algébrique, Chapitres 1 à 4, Springer, 2016. doi:10.1007/978-3-662-49361-8, ISBN 978-3-662-49361-8.
1 to 68 of 68