nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
nLab > Latest Changes: Galois theory/bar path oo-groupoid of an oo-stack
Bottom of Page1 to 53 of 53
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 7th 2010
- (edited Feb 7th 2010)
(edit: typo in the headline: meant is "bare" path oo-groupoid)
I think I have the proof that when the structured path oo-groupoid of an oo-stack oo-topos exists, as I use on my pages for differential nonabelian cohomology, then its global sections/evaluation on the point yields the bare path oo-groupoid functor, left adjoint to the formation of constant oo-stacks.
A sketch of the proof is now here.
Recall that this goes along with the discussion at locally constant infinity-stack and homotopy group of an infinity-stack.
P.S.
Am in a rush, will get back to the other discussion here that are waiting for my replies a little later. Just wanted to et this here out of the way
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeFeb 7th 2010
This looks like having some similarity in intuition related to HTT Theorem 7.1.0.1.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeFeb 8th 2010
- (edited Feb 8th 2010)
Thanks for alerting me of that theorem. I had seen it before, but missed its meaning.
I think this is indeed Toen's theorem, again, in slight disguise!
Let's just use slightly different symbols to make this more explicit:
on the left Lurie has
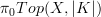 . But that's the same as
. But that's the same as 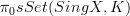 .
.And we may write
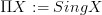 , so that the left side then may be written
, so that the left side then may be written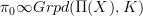 .
.On the right side, we have in the notation used on our nLab entries
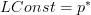 and
and 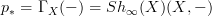 .
.So using the notation this way, the theorem says
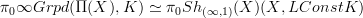 .
.As we have discussed, this is Toen's theorem! In fact it is weaker than that, because Toen actually (slightly implicitly as we have discussed) proves a full equivalence of oo-categories
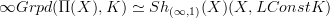 .
.Okay, that's good to know. I'll add this remark to our blog entry.
But notice that what I am trying to get at on my web is something more: I want to see when this holds not just over topological spaces, but over general objects of an oo-topos. I want to generally see
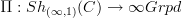 as a left adjoint to
as a left adjoint to 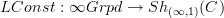
I suspect this left adjoint should exist quite gnerally, but am too stupid at the moment to prove it in that generality. But I think I can prove it now for all oo-toposes that are "path structured oo-toposes" as discussed on my web. In these cases the
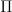 that I built using the interval object is actually (or its global sections are) this canonically defined left adjoint
that I built using the interval object is actually (or its global sections are) this canonically defined left adjoint 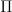 . I think
. I think -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeFeb 8th 2010
- (edited Feb 9th 2010)
I have now put the above comment into the entry homotopy group of an infinity-stack here in the last subsection.
I have also reorganized this now a bit. I start this subsection now by staing clearly what I think the theorem is, that is established in the literature (including Toen, Shulman, Cisinski, Lurie) highlighting a certain formulation of it. Then I go through the references and discuss a bit how these indeed show this.
However, I only looked into Toen and Lurie's statement in more detail. My impression is that Mike's and Denis-Charles is a different way to say the same statement (but please correct me, I haven't really absorbed this). Lurie shows something a bit more general, I think, but only under
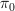 . So I say this, too.
. So I say this, too.One aspect that should be discussed further is the claim that indeed morhisms
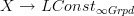 are locally constant oo-stacks on X. For 2-stacks this is explicit in Waschkies et al. I think for oo-stacks it is clear, too, but maybe "is clear" should be substantiated a bit more.
are locally constant oo-stacks on X. For 2-stacks this is explicit in Waschkies et al. I think for oo-stacks it is clear, too, but maybe "is clear" should be substantiated a bit more. -
- CommentRowNumber5.
- CommentAuthorzskoda
- CommentTimeFeb 8th 2010
impressive
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
Thanks, Zoran, I am enjoying the nice statement that comes out here. You know, I was going to ask you if you could teach me a bit about the "Yoga of 6 functors". Because the statement now will be that we have for
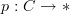 the three canonical functors
the three canonical functors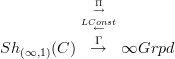
Now I would like to know what happens when this Yoga of 3-functors is extended to the full Yoga of 6 functors!
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
David,
thanks, I see your comment on the nicety conditions on
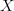 . I meant to go again carefully through the articles and extract this. Waschkies et al for instance claim they need less assumptions than Toen. Lurie just requires paracompactness.
. I meant to go again carefully through the articles and extract this. Waschkies et al for instance claim they need less assumptions than Toen. Lurie just requires paracompactness.All help in sorting this out is appreciated.
-
- CommentRowNumber8.
- CommentAuthorDavidRoberts
- CommentTimeFeb 9th 2010
I added a caveat to the last section about oo-stacks on Top - as is pointed out by Toen (I think) one needs the base space to be locally contractible, in the sense that there is a basis of open sets whose inclusions are null-homotopic. From the point of view of the fundamental oo-groupoid, this means the inclusion Pi(U) -> Pi(X) is naturally isomorphic to the zero map. This is necessary to locally trivialise the locally constant stack.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
Oh, and I need to sort out equivalences of oo-groupoids of locally constant stacks versus equivalences of just oo-groupoids. Toen has the stronger statement, even, unless I am mistaken.
-
- CommentRowNumber10.
- CommentAuthorDavidRoberts
- CommentTimeFeb 9th 2010
Polesello-Waschkies only need 2-dimensional conditions, as they are treating 1-stacks, but as Toen is treating oo-stacks, he needs local homotopy conditions for all dimensions. I have 'Toen-conditions' in my thesis for some bits and 'Polesello-Waschkies-conditions' for other bits, so there are some subtleties I felt I hadn't 100% resolved in my theory.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
Oh, I see.
So can you help mee here with "locally (relatively) contractible" as opposed to "paracompact"?
You should create an entry for "locally (relatively) contractible" and link to it! :-)
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
Oh, wait, Toen does just oo-groupoids after all. Hm, let me check...
-
- CommentRowNumber13.
- CommentAuthorDavidRoberts
- CommentTimeFeb 9th 2010
We have well-connected space (which needs expanding) I created for this purpose a while ago.
The paracompactness asumption of Lurie is probably like when one has a soft sheaf for coefficients, so when the base space is paracompact, the sheaf is acyclic. It is the acyclicity which is the desired result, not the softness as desired input. This is only a guess, though.
-
- CommentRowNumber14.
- CommentAuthorDavidRoberts
- CommentTimeFeb 9th 2010
Now added locally contractible space, and added a conjecture about locally constant n-stacks
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
Thanks David,
I added some editorial sugar to the entry. Will think about it.
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
I should add the following observation somewhere, simple but useful in this context:
the constant sheaf functor has a left adjoint which is taking connected components of the etale space of a sheaf (i.e.
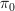 )
)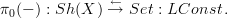
Unless I am mixed up, this is a simple observation, but it might deserve highlighting. it follows for instance by looking at the naturality diagram of a morphism
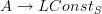 over morphisms that include a germ of open subsets into an open subset. One sees that these are determined by the value on the stalk.
over morphisms that include a germ of open subsets into an open subset. One sees that these are determined by the value on the stalk.Equivalently one can see that
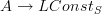 is a morphism of the coresponding etale spaces from that of
is a morphism of the coresponding etale spaces from that of  to the one that is simply
to the one that is simply 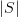 copies of X.
copies of X.Well, as I said, either I am mixed up or this is a well known familiarity. But it is sort of noteworthy that we have this here: the left adjoint to
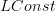 is
is 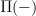 . For 0-stacks aka sheaves this is
. For 0-stacks aka sheaves this is 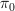
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
I added now an examples-section Geometric Pi_0 of sheaves on topological spaces.
I give a simple argument -- just so as to amplify the general pattern -- that for categories of sheaves on a topological space, the constant-sheaf functor does have a left adjoint
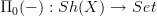 which sends a sheaf to the set of connected components of its etale space.
which sends a sheaf to the set of connected components of its etale space.Notice that
for the special case of the terminal sheaf -- i.e. the underlying topological space itself -- this is a special case of the statements for topological spaces that follow...
but that this goes further in that it really gives
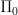 of a general object in the topos. And the answer is the expected one: the "generalized space modeled on Op(X)" that a sheaf represents is its etale space, so the geometric oth homotopy set of the sheaf should be that of its etale space.
of a general object in the topos. And the answer is the expected one: the "generalized space modeled on Op(X)" that a sheaf represents is its etale space, so the geometric oth homotopy set of the sheaf should be that of its etale space.
The argument is of course very elementary. I would still like to see this mentioned in the literature.
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
so with the idea stabilizing that a good definition of the homotopy groups of an object
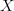 in a general oo-topos is given by the oo-groupoid
in a general oo-topos is given by the oo-groupoid 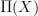 for
for 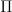 left adjoint to the constant oo-stack functor, I would like to now describe the Galois-theoretic approach from this perspective.
left adjoint to the constant oo-stack functor, I would like to now describe the Galois-theoretic approach from this perspective.So I added now one more section: By monodromy that describes how from the existence of a left adjoint to
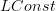 it follows that the geometric homotopy oo-group of
it follows that the geometric homotopy oo-group of 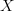 sits inside the oo-group of automorphisms of the fiber functor
sits inside the oo-group of automorphisms of the fiber functor 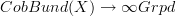 .
.I guess, as indicated there, that one can see that this inclusion is in fact an equivalence, but I haven't yet found general fully formal argument for that.
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
Oh, now I see, this Galois theory business is just the oo-Yoneda lemma:
the fiber functor
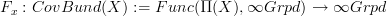
by the oo-Yoneda lemma applied to presheaves on
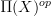 may be thought of as
may be thought of as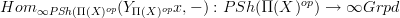
(where
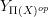 denotes the Yoneda embedding into presheaves on
denotes the Yoneda embedding into presheaves on 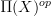 )
)because it is just evaluation of a local system on the chosen basepoint
 .
.Then again by oo-Yoneda, but now applied to presheaves on (presheaves on
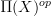 )^op we find that
)^op we find that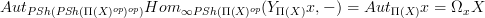
QED.
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
Let's see. What am I saying? I am saying that Tannakian reconstruction is just the Yoneda lemma applied twice.
Am I mixed up?
-
- CommentRowNumber21.
- CommentAuthorTim_Porter
- CommentTimeFeb 9th 2010
I just checked up. Local contractibility as defined in Spanier (p. 57) is the relative form. (Perhaps this needs a small comment in one of the entries.)
Ages ago (in my thesis) I showed that a locally contractible space (in the non-relative definition) was 'stable', which meant that the proobject of Cech nerves for it was isomorphic in the category pro-Ho(SimpSet) to a constant pro-object. There are some quite subtle relationships between the local relative contractibility condition and the shape of the space, and I am wondering if somehow it is not something related to that which is coming into play in the general case.
-
- CommentRowNumber22.
- CommentAuthorTim_Porter
- CommentTimeFeb 9th 2010
I should remember an example of a space that is locally relatively contractible but not locally contractible. I would need to look back at papers from the 1970s in Shape Theory. and do not have them with me. Sibe Mardesic would know (and Zoran might be able to find out or may know.)
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
here now the writeup of what currently to me looks like the proof that the right geometric homotopy oo-groups are obtained from the automorphisms of the fiber functor on locally constant oo-stack:
-
- CommentRowNumber24.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
I can not answer to the cafe as I am blo?cked but I am not satisfied with your answer quoting Lurie 7.1.4.3 and 7.1.4.4. as the proper generalization (look at my empahsis in the question which asked for NO equivalent categories but genuine generalization at point-set topology level). First of all one needs to take at the left hand side fibered (infinity,n)-categories, not only (infinity, 1)-sheaves. On the left hand side one should look at weak (infty,n)-categories internal to Top. Then one should have adjoint (infty,n)-pair. It is not the plus construction efefctively the sheafification but n times in (infty,n)-context. For example, Street has proved you need three times for the stackification of 1-stacks.
Finally it is important that general topology works for general topologies, as it is with etale spaces. Not only paracompact Hausdorff up to WEAK topological type what simplicial model can afford hence Lurie's theorem in simplicial world.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
It is not the plus construction
Well, there are two things maybe called the +-construction. Maybe that wasn't precise use of terminology:
what I mean is this: you can sheafify a presheaf by first constructing its etale space and then taking the sheaf of sections of that.
What Lurie proves in the theorems I pointed to is exactly the
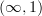 -version of this.
-version of this.For example, Street has proved you need three times for the stackification of 1-stacks.
Yes, I think that's known in full generality. Beke shows in his "Higher Cech theory" that you need to apply
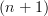 -step hypercovers, instead of just covers (my counting might be off by 1 or so). I think Luire discussesthe same statement in HTT somewhere.
-step hypercovers, instead of just covers (my counting might be off by 1 or so). I think Luire discussesthe same statement in HTT somewhere.I am not satisfied with your answer quoting Lurie 7.1.4.3 and 7.1.4.4. as the proper generalization
Okay, then I maybe don't understand what exactly you want. Could you write out for me the formal would-be statement that you have in mind?
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
Coming back to the fundamental oo-groupoid of an object in an oo-topos:
after discussion with Ieke today, it turns out that the statement that I keep trying to drive at at homotopy group of an infinity-stack and the constructions now on my web at path oo-groupoid are (slightly implicitly) already known by people in "classical topos" theory who would work with simplicial objects in a topos without making the model structure on these explicit, but doing implicitly precisely the right thing.
I have now a bunch of further relevant references, which I will work into the entry, but this one here is the one with the major statement:
Ieke Moerdijk, Classifying spaces and classifying topoi Lectrues notes in Math 1616, Springer (1991)
The crucial section is 1.4, starting on p. 15. If you look closely, you see that the second displayed equation on p. 18 is precisely (after the required translation of notation and models) the action of
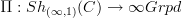 that I discuss on my web: you take a simplicial sheaf X, pass to a cofibrant replacement that is degreewise a coproduct of contractible representables (a "good cover") and then replace all these representables by points. The result is a constant simplicial presheaf hence a simplicial set. That's
that I discuss on my web: you take a simplicial sheaf X, pass to a cofibrant replacement that is degreewise a coproduct of contractible representables (a "good cover") and then replace all these representables by points. The result is a constant simplicial presheaf hence a simplicial set. That's 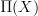 .
.On that page 18 there is no notion of of cofibrancy, instead there is a colimit taken over covering objects. But by the standard reasoning such as in Kenneth Brown's thery of category of fibrant objects that boils down to the same thing: the colimit will find the cofibrant replacement and by the property of cofibrancy will localize there.
Anyway, if you know this stuff, this is pretty obvious, if that sounds cryptic then don't worry, I'll write this out now in detail in the nLab entry homotopy group of an infinity-stack.
And by the way, as the entry is growing and all the concepts and results in the literature turn out to be now nicely converging, I am inclined to rename the entry. I am thinking of
- homotopy groups in an (oo,1)-topos
or just
- homotopy in an (oo,1)-topos
or maybe even just
- homotopy
replacing and incorporating the entry that currently goes by this name suitably.
I am thinking that we see now that have here a discussion "homotopy from the nPOV in full generality in any (oo,1)-topos" that nicely parallels the analogous discussion at cohomology. So that's why I would enjoy having a pair of entries called just cohomology and just homotopy .
-
- CommentRowNumber27.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
Could you write out for me the formal would-be statement that you have in mind?
I wrote it above. Take ANY topological space X, not necessarily paracompact Hausdorff, and then take appropriate weak n-category (not just simplicial localization or simplicial nerve, what just says simplicial image as (infinity,1)-cat) internal to Top/X (Top includes again all spaces, not some simplicial category which takes care only of weak homotopy type). Then on the right hand side you take Fibered n-categories over Ouv(X). There is an adjunction between the two etc. You just write things about SIMPLICIAL NERVE, so you LOOSE the topology beyond weak homotopy type.
Edit (clarification): In fact Top/X should be replaced by n-category of internal (n-1)-categories in usual 1-categorical Top/X on the left, or a variant thereof, if I wasn't clear enough. Etale 2-space should be a special object there for n=2.
-
- CommentRowNumber28.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
Yes, I think that's known in full generality. Beke shows in his "Higher Cech theory" that you need to apply (n+1)-step hypercovers
Thanks for reminding me, though I think it is also just the groupoidal case. For n=2 already you can tell much more (Igor for example spend months on this).
Lurie's theorem is an analogue, but not a generalization. And this is seen in many important aspects, lost in Lurie's version. Maybe infinity version of ionads would be better approach.
-
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
oh, I see, you want the statement for
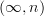 -sheaves for
-sheaves for 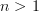 . Okay, right, that's something more general.
. Okay, right, that's something more general.Of course we can ask for that more general statement, too. But let's maybe just highlight what Lurie's theorem there achieves: it tells you what an "n-etale space" is for all n and how it relates to
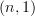 -sheaves. That's pretty cool already.
-sheaves. That's pretty cool already. -
- CommentRowNumber30.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
In a way, Lurie's statement is just a derived shadow of the true statement which should deal with internal omega categories and omega presheaves over Top. There s a general external - internal point of view: internal ctageories vs. presheaves, but here that adjunction gets a more detailed content when we retsrict to stacks and the left hand side can be characterised in descriptive toplogical terms.
-
- CommentRowNumber31.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
oh, I see, you want the statement for (\infty,n)-sheaves for n > 1. Okay, right, that's something more general.
Am I speaking Korean ?? This is true that I want for higher n, but not only that I want that it is a TRUE generalization, not analogue. So we have to recover n=1 case with full power. Even for n = 1 Lurie's statemet does not cover the classical case. It covers just the weak homotopy type version and forgets about the details of the space. It gets derived from the start.
-
- CommentRowNumber32.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
Lurie's theorem there achieves: it tells you what an "n-etale space" is
No, it does not. Even for n=1. It just says what is its derived image.
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
Are you sure about this? The weak equivalence of an ordinary etale topological space over X seem to me to be the ordinary isomorphisms. Since the morphisms have to be over X the weak equivalences in
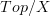 are stalk-wise weak equivalences. Since the stalk of an etale space is a set, this are just the isomorphisms in this case.
are stalk-wise weak equivalences. Since the stalk of an etale space is a set, this are just the isomorphisms in this case. -
- CommentRowNumber34.
- CommentAuthorMike Shulman
- CommentTimeFeb 10th 2010
I'm not really following this, but I wonder if the "Latest Changes" area of the n-Forum is really the best place to have this discussion?
-
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
That's right. I think Zoran is posting here because he currently cannot post on the blog. But it is true that we should move this elsewhere. Either back to the blog, or to a thread on an nLab entry that discusses this.
-
- CommentRowNumber36.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
he currently cannot post on the blog
for almost a month already, unless I am not at work (at home it is OK)
I am not getting precisely (just vaguely) this theorem about stalkwise weak equivalence, but anyway the adjoint pair is not only for etale spaces; only the restriction which is an equivalence is. Therefore you might be right that the very etalification can be expressed only as a corollary of the Lurie's theorem, but not the whole precise adjoint relationship between the internal and external point of view. I think that the point-topological information which is lost after taking simplicial localization is lost, even if the etalification for the representing members of weak homotopy classes is faithful as you say. Edit: even more I am not sure if the statement about weak equivalence for the essential image in the Lurie's theorem can easily be shown to have the same weak equiv thus iso property as we know for the usual picture of etale spaces, or more appropriately, the internal n-categories in etale spaces. The identification if it can be done, would resolve big part of my compliant.
-
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
this theorem about stalkwise weak equivalence
Look at it on the right side of the equivalence:
a weak equivalence of simplicial presheaves on a paracompact topological space is one that is stalkwise a weak equivalence of simplicial sets. If the simplicial presheaves in question happen to be set-valued, i.e. happen so be ordinary simplicial presheaves, then stalkwise weak equivalences are just stalkwise isomorphisms of simplicial sets. So weak equivalences between oo-stacks that happen to be ordinary sheaves are ordinary isos of sheaves.
Now the equivalence tells us that these stalks are the fibers of an etale space over the given point, and hence that the weak equivalences between these etale spaces (over X) are just ordinary isos of etale spaces.
-
- CommentRowNumber38.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
not the whole precise adjoint relationship between the internal and external point of view.
Could you remind me precisely what this adjoint relationship refers to?
-
- CommentRowNumber39.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
If you have a category with pullbacks, then internal categories correspond to presheaves of categories; and all possible categorifications and strengthenings of it (but here sizes may matter). I thought that this could be combined with the usual 1-categorical statement on etale spaces to some benefit.
Look at it on the right side of the equivalence:
The right hand side is simplicial, I mean no localization is done, just taking simplicial presheaves. The left hand side is the one which has information on potentially bad local topology. Any space over X. Now in a weak homotopy class which is sense at the level of simplicial localization the class of an etale space contains also many representatives which are very different in the sense not felt by weak homotopy type and by simplicial model. These ones worry me. Lurie is having a statement about weak homotopy type not about genuine Top/X.
So weak equivalences between oo-stacks that happen to be ordinary sheaves are ordinary isos of sheaves.
What guarantees that if you start with an etale space take its image in simplicial nerve of Top/X do Lurie adjunction and return back to the simplicial nerve, that you will get back a weak homotopy class of an etale space ? Even more for internal n-categories in etale spaces for higher n. This would need to have some statements about how etale spaces and their higher categorical combinations sit inside the simplicial nerve of Top/X. In particular, it should distinguish well etale n-spaces from other representatives of their weak homotopy types, what is not internal notion within the simplicial localization. I do not see how you can avoid at least some set theoretic topology eventually.
-
- CommentRowNumber40.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
Let's do the eale spaces first. I have trouble seeing what flexibility you seem to see.
we have two etale spaces E1 and E2 over X regarded as objects in Top/X. Any morphism between them is a morphism of spaces over X. That means it has to be a map of the total spaces such that for each point x in X the fiber E1_x is mapped to the fiber E2_x .
If the morphism is an equivalence, this must be an isomorphism for each fiber, evidently, because in Top/X everything must work fiberwise. So equivalences of etale spaces regarded as objects in the oo-category Top/X are just ordinary isos of etale spaces.
Or what am I missing?
-
- CommentRowNumber41.
- CommentAuthorDavidRoberts
- CommentTimeFeb 11th 2010
Zoran wrote:
Edit (clarification): In fact Top/X should be replaced by n-category of internal (n-1)-categories in usual 1-categorical Top/X on the left, or a variant thereof, if I wasn't clear enough. Etale 2-space should be a special object there for n=2.
As in my thesis :)
Urs wrote:
If the morphism is an equivalence, this must be an isomorphism for each fiber, evidently, because in Top/X everything must work fiberwise. So equivalences of etale spaces regarded as objects in the oo-category Top/X are just ordinary isos of etale spaces.
but a fibrewise isomorphism does not imply an isomorphism of etale spaces.
a weak equivalence of simplicial presheaves on a paracompact topological space is one that is stalkwise a weak equivalence of simplicial sets.
but if we are interested in more than just paracompact spaces?
-
- CommentRowNumber42.
- CommentAuthorUrs
- CommentTimeFeb 11th 2010
but a fibrewise isomorphism does not imply an isomorphism of etale spaces.
Okay, I am probably mixed up, then. What's an example of a morphism in Top/X between two Etale spaces that's not a morphism of Etale spaces?
but if we are interested in more than just paracompact spaces?
The theorem byy Lurie that we are talking about uses the assumption of paracompact base space. Without that, we don't have that theorem.
-
- CommentRowNumber43.
- CommentAuthorDavidRoberts
- CommentTimeFeb 11th 2010
I'm probably mixed up too.
What's an example of a morphism in Top/X between two Etale spaces that's not a morphism of Etale spaces?
welll... they are are the same thing. I'm probably not quite familiar with the sheaf/stack side of things, and I was taking the statement about fibrewise iso/equivalence to mean that fibre by fibre there is an iso/equivalence (not induced by a morphism of etale spaces). This is clearly false, but if you didn't mean that, then I apologise for being dense.
For the second point I was going from Zoran's comment
Take ANY topological space X, not necessarily paracompact Hausdorff, and then take appropriate weak n-category ... internal to Top/X
and I agree that the assumption of paracompactness is for homotopy theory too strong. To me this says that we should be looking for another theorem going beyond Lurie's, if this is possible.
edit: I was going to discuss Lurie's technical requirements for paracompactness, but this is better to be done on the page itself.
-
- CommentRowNumber44.
- CommentAuthorUrs
- CommentTimeFeb 11th 2010
Okay. You know, morphisms of etale spaces are usually defined to be the morphisms in Top/X between etale spaces. Etale spaces are defined as a full subcategory on Top/X on which a certain adjunction produces an equivalences. Isn't that actually the starting point of all of the discussion here?
-
- CommentRowNumber45.
- CommentAuthorDavidRoberts
- CommentTimeFeb 11th 2010
I got the wrong end of the stick by skimming over the profusion of comments that came up during yesterday. I think I read this (by you, Urs)
weak equivalences in Top/X are stalk-wise weak equivalences.
and got confused. I'm wasn't sure what you mean by a stalk-wise weak equivalence for a map in Top/X. If you mean fibre homotopy equivalence then I agree. I just thought there was some tricky passing to stacks or something that was implicit - I'm probably just confusing myself.
morphisms of etale spaces are usually defined to be...
yeah, I know (wry grin). I haven't lost all my marbles.
-
- CommentRowNumber46.
- CommentAuthorUrs
- CommentTimeFeb 11th 2010
Okay, no, that's good, don't worry. Sometimes one just needs to sync into each other's frequency, even if the item under discussion is clear to everyone internally.
-
- CommentRowNumber47.
- CommentAuthorzskoda
- CommentTimeFeb 11th 2010
The paracompactness is a minor point and my complaints were more serious.
Okay. You know, morphisms of etale spaces are usually defined to be the morphisms in Top/X between etale spaces.
Yes, but Lurie's theorem is not about Top/X but about its simplicial nerve. So zig zags are also allowed in the story; plus Lurie's theorem does not say (as I wrote about several times already) that doing the adjunction back and forth can be strictified in such a way that starting with etale space you get again an etale space. In fact his theorem does not say anything about etale spaces, because the category of etale spaces is not at either side of his adjunction. Just we know indirectly that WEAK homotopy types of etale spaces should correspond to a sub-infty,1-category at the left side.
-
- CommentRowNumber48.
- CommentAuthorUrs
- CommentTimeFeb 11th 2010
- (edited Feb 11th 2010)
but Lurie's theorem is not about Top/X but about its simplicial nerve. So zig zags are also allowed in the story;
So you have a zig-zag of isomorphisms of etale spaces then. That's still an isomorphism of etale spaces.
In fact his theorem does not say anything about etale spaces, because the category of etale spaces is not at either side of his adjunction.
Well it is the subcategory in Top/X that is in the image of the oo-sheaves that are set-valued.
And what the theorem does on top of this is to say what the higher analogs of etale spaces are: namely the image in Top/X of n-groupoid valued sheaves in Sh_oo(X).
Just we know indirectly that WEAK homotopy types of etale spaces should correspond to a sub-infty,1-category at the left side.
I am not sure what else I can say in reply to this. Do we agree that an zig-zag of weak equivbalences between etale spaces in Top/X is just an iso of etale spaces? Because each weak equivalence in the zig-zag is. This is like saying that a weak equivalence between two sets cannot be anything but an isomorphism of sets. A zig-zag of weak equivalences of sets is still just an isomorphism of sets. An etale space is like a set in Top/X: it is an object in there that is fiberwise a set.
-
- CommentRowNumber49.
- CommentAuthorzskoda
- CommentTimeFeb 11th 2010
So you have a zig-zag of isomorphisms of etale spaces then. That's still an isomorphism of etale spaces.
The first one is etale space, the other spaces in zig zag are not necessarily etale, nor we can guarantee that the last one is if the first one is without stating more preciuse form of a theorem.
-
- CommentRowNumber50.
- CommentAuthorzskoda
- CommentTimeFeb 11th 2010
You see, you are trying to talk about various PARTS of left and right hand side of adjunction at infinity level, as if we had faithful inclusions (but everything is just up to homotopy) and we do not know that the natural functors (which are not 1-categorically faithful) are compatible with the adjunction. Simplicial nerve can not even SEE the details which are beyond simplicial models, nor a quillen equivalence can. The fact that you need assumptions like paracompactness means you do preparation for doing just weak homotopy information.
No, I do not agree that zig zag starting with an image of etale space in simplicial nerve and ending in some other object in the simplicial nerve is an equivalence of etale spaces. And even if it is, it does not describe the infintge catgeorical analogues in topological terms, but in terms of simplicial localization.
-
- CommentRowNumber51.
- CommentAuthorzskoda
- CommentTimeFeb 11th 2010
An etale space is like a set in Top/X: it is an object in there that is fiberwise a set
It is a good intuition but no refinements of that intuition are supplied by Lurie's theorem.
-
- CommentRowNumber52.
- CommentAuthorUrs
- CommentTimeFeb 11th 2010
Take X to be the point, for a moment. Then the equivalence becomes that between topologivcal space and simplicial sets. The statement is that the geometric realization of a simplicial set that is just a set is a discrete topological space. An etale space over the point. The weak equivalences between such etale spaces over the point are just isomorphisms of sets.
Do we agree on this? Since the general situation is in the overcategory, it is an X-parameterized version of this situation.
-
- CommentRowNumber53.
- CommentAuthorzskoda
- CommentTimeFeb 11th 2010
I think we agree on this, I understand this, just the adjunction between simplicial nerve does not need to know of choices in weak homotopy classes unless you prove something more specific. But never mind, we can talk about that some time in future.
1 to 53 of 53