nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
created Tannaka duality
with a short proof of the duality for the category of permutation representations of a group, using the Yoneda lemma three or four times in a row and nothing else.
either I am mixed up (in which case we'll roll back), or I guess this is the way that it's usually done in the literature? I haven't really checked. Sorry, I just needed that quickly as a lemma for my discussion at homotopy group of an infinity-stack
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
of course I am happily ignoring all size issues...
-
- CommentRowNumber3.
- CommentAuthorzskoda
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
In any case all reconstruction theorems do boil down to various embedding and ro descent theorems like Barr embedding, Yoneda lemma, Yoneda plus monadic structure etc. and their reconstructions (EDIT: this is a typo I meant and their LINEARIZATIONS). Among general tannakian reconstruction theorems there are two most classical -- one called Tannaka's theorem and one called Krein's theorem. What you call Tannaka theorem is not THE Tannaka's theorem but one of the many in the modern series of tannakian, not Tannaka's reconstruction, I think.
Edit: I mean your work is great, but we should distinguish generic term Tannakian from specific Tannaka, which corresponds to a specific linear case (if I remember right the duality between a class of Hopf algebras and a class of monoidal categories but I am not sure about correct generality). The difficult Tannakian cases are those of noncommutative Hopf algebroid, and also when there is no single fiber functor but a whole stack, the latter being relevant for mixed motives.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeFeb 9th 2010
Okay, we'll sort it out.
In any case I started a section Applications at Yoneda lemma, which we might eventually expand to a useful list.
-
- CommentRowNumber5.
- CommentAuthorzskoda
- CommentTimeFeb 9th 2010
- (edited Feb 9th 2010)
I added a comment more in edit above. There is a famous paper of Ulrich, for coalgebras etc. and also of course Deligne for mixed case. There are version with difficult functional analysis. Rosenberg wrote a much simpler proof of Deligne's theorem in another paper and also a generalization in functional context in yet another. I can not work much on this tomorrow as I have to prepare my lecture which i am not yet ready for.
The case with a single fiber functor is called the case of a neutral Tannaka category.
-
- CommentRowNumber6.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
I am taking it back, partially! I went to sleep after I wrote it and realized that the entry has title Tannaka DUALITY and not Tannaka THEOREM. Of course Tannaka theorem is a theorem on Tannaka duality. But, while Tannaka theorem is a technical term just for one specific instance of Tannakian reconstruction theorems, the very phenomenon of that duality is interchangeably, and justifiably called Tannaka duality or Tannakian duality. While there are many Tannaka duality theorems, and just one Tannaka theorem, for each particular category of beings there is more or less just one thing which is Tannaka duality for that class of beings.
Another issue: mixed Tannakian categories lead to groupoids instead of groups. But the groupoid in question is algebraic and just a presentation of a gerbe! Hence once one say "mixed" (liek mixed motive) one has higher categorical cocycle in the game directly or indirectly. I do not knwo if this is a useful remark for Urs's effort at understanding Toen's and other categorifications of Tannaka duality.
-
- CommentRowNumber7.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
There are no size difficulties here. The Yoneda lemma applies to representable functors
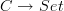 if
if  is locally small, so it applies when
is locally small, so it applies when  is the category of permutation representations
is the category of permutation representations 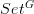 .
.I agree that (in this simple case) the result is just a simple application of Yoneda. I also felt that some abuse of notation would make the argument look easier. The underlying functor
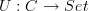 is the representable
is the representable 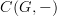 , and the argument is that
, and the argument is that 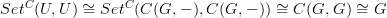 , where
, where 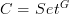 . The '
. The ' ' is used in multiple senses, but presumably each sense is deducible from context.
' is used in multiple senses, but presumably each sense is deducible from context. -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
There are no size difficulties here.
Oh, right, thanks. I am always a bit worried that I may be missing size issues. :-)
Thanks for looking into this.
I agree that (in this simple case) the result is just a simple application of Yoneda.
Okay, thanks for the check. I suppose that must be obvious and well known, but I hadn't thought of it that way when it suddenly struck me. So I thought it would be nice to just note it down.
And sure, I understand that this is the very simple case of the reconstruction. But it happens to be the full "explanation" for what is needed in oo-Galois theory where automorphisms of the fiber functor from locally constant oo-stacks are considered. So while simple, it does yield something that may be inherently trivial -- but looks impressive! :-)
I also felt that some abuse of notation would make the argument look easier.
Right, yes, I agree. My note was aimed at making myself clear to you all, more than being an exposition. Now with the statement cross-checked, we should make the exposition in the entry more readable.
-
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
I editet Tannaka duality a bit and inserted Todd's way of writing the proof, from above.
-
- CommentRowNumber10.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
I like it. If I had more time I would add some things in nonsymmetric nonstable world. But it will have to wait, unfortunately...
-
- CommentRowNumber11.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 10th 2010
I made a minor edit to make the "
 " part go smoother.
" part go smoother. -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
Thanks, Todd. I was thinking of this an hour or so back, too, but then got distracted.
Do you know if now given this nice proof we can with similar little effort go on and discuss the next-simplest case of Tannaka-duality?
Well, first of all it is a direct corollary now to get the reconstruction of groupoids from their "permutation representations". I can maybe put that in later.
But what about going to other representations? Are there useful cases that still just follow from simple abstract reasoning?
-
- CommentRowNumber13.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
All cases of Tannaka boil down to cases of general nonsense. Rosenberg wrote an article on fiber functors in which he shortens even the Deligne's proof to only several pages of general nonsense plus linear algebra.
-
- CommentRowNumber14.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
We should also look at lectures of Street and also of Joyal ad Street in Como for alternative gemneral nonsense treatments. If anybody needs there is a file pf the whole Como. Here is just their contribution:
AN INTRODUCTION TO TANNAKA DUALITY AND QUANTUM GROUPS by André JOYAL and Ross STREET, pdf
I'll put it in nlab.
-
- CommentRowNumber15.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 10th 2010
Zoran beat me to it: the Joyal-Street notes are perhaps the next thing to examine. I don't believe they invoke Yoneda explicitly, but one should read between the lines.
-
- CommentRowNumber16.
- CommentAuthorzskoda
- CommentTimeFeb 10th 2010
- (edited Feb 10th 2010)
I remember that they talk much about coends and stuff. I read parts long ago, with only partial understanding. I have now entered few references and links to Tannaka duality. Hope it helps. But now I should really take a bus to arrive home not too late for very late dinner...
Edit: added redirect Tannaka reconstruction.
Edit: could not stand and wrote Tadao Tannaka and missed next bus.
-
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeFeb 10th 2010
could not stand and wrote Tadao Tannaka and missed next bus.
Thanks! You win the nLab-True-Dedication-Award, though! :-)
-
- CommentRowNumber18.
- CommentAuthorzskoda
- CommentTimeApr 20th 2010
- (edited Apr 20th 2010)
New reference today at arxiv on derived Tannaka and qcoh sheaves, in the language of quasicategories, entered into Tannaka duality. Another reference today on the arxiv "What is a perverse sheaf ?" at perverse sheaf.
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeMay 15th 2010
- (edited May 15th 2010)
concerning the Yoneda-lemma-proof of Tannaka-reconstruction for permutation representations that we discuss at Tannaka duality:
don’t we have a much more general statement by simply observing that the proof given there in Set goes through verbatim in -enriched category theory over any ?
Notably for , where, unless I am overlooking something, the proof tells us the the endomorphism algebra of the forgetful functor is isomorphic to .
Then for a group, let be its group algebra, so that . Then the Yoneda-proof shows that the endomorphism algebra (in the sense of Vect-enriched category theory) of is the group algebra of . Doesn’t it?
-
- CommentRowNumber20.
- CommentAuthorTodd_Trimble
- CommentTimeMay 15th 2010
- (edited May 15th 2010)
Urs: yes. In fact, why not replace a group by a monoid? I’ll write up something at Tannaka duality.
Edit: oh, I see you already did precisely that. Looks good.
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeMay 15th 2010
yes. In fact, why not replace a group by a monoid?
Yes, i was thinking about that, too. And more so, we can also discuss the case of groupoids and algebroids.
Right, so thanks for the sanity check. Unless somebody blocks the entry before me, i will now expand it considerably.
How hard might it be to extend this abstract-nonsense proof to one of Doplicher-Roberts reconstruction? We would want to show that for a symmetric monoidal -category with maybe some suitable extra assumptions, and for
a symmetric monoidal -enriched functor, we have .
That would be the statement of DR-reconstruction.
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeMay 15th 2010
- (edited May 15th 2010)
I am now a bit puzzled about the sociological status of our statement here. Are we the first to have observed that Tannaka duality is nothing but the Yoneda lemma? If not, where is this mentioned in the literature? I am scanning through
Joyal-Street, An introduction to Tannaka duality and quantum groups
One would think if any text mentions the relation then this one. But it does not seem to do so. (Though I have to admit that I only skimmed it very briefly. Maybe it does say something. But searching the document for “Yoneda” gives only a single hit in a proof, where it seems to be unrelated to what we are talking about here.)
-
- CommentRowNumber23.
- CommentAuthorTodd_Trimble
- CommentTimeMay 15th 2010
I’ll respond to this in a bit. Meanwhile, why did you write over my enriched Yoneda lemma? I was busy getting that into shape.
-
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeMay 15th 2010
Meanwhile, why did you write over my enriched Yoneda lemma? I was busy getting that into shape.
Oops, didn’t see that. Didn’t know you were writing it. let’s roll back things..
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeMay 15th 2010
Todd,
I rolled back to your version and edited a bit.
-
- CommentRowNumber26.
- CommentAuthorTodd_Trimble
- CommentTimeMay 15th 2010
Okay, thanks. Also, I was going to write enriched natural transformation. :-)
It seems the form of Tannaka duality Joyal and Street start off with is where is a topological monoid and the representations are finite-dimensional, so they don’t quite have the luxury of representability that we have on the nLab page. That’s a first pass at what’s going on. There are other issues that I want to think about before saying anything further…
-
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeMay 15th 2010
- (edited May 15th 2010)
I see, thanks.
Meanwhile, I had chance to work on Tannaka duality and have expanded it now considerably. With always the same rpoof again and again, I try to list interesting cases that follow as special cases without further work
I am being hurried now, we go and visit some friends, so I haven’t proof-read this as I should. Got to run now.
-
- CommentRowNumber28.
- CommentAuthorTodd_Trimble
- CommentTimeMay 15th 2010
Of course, this is a simple conceptual (or abstract-nonsense) explanation of Tannaka duality, and right now it looks like it could be a stand-alone page. I’m trying to think whether (or how) an account of classical Tannaka duality, as described say by Joyal-Street, would fit on this page. Should a separate page be written, or should this page be reorganized so that this Yoneda lemma account is named “abstract Tannaka duality” (or something)?
-
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeMay 15th 2010
Yes, I was wondering about that, too.
Maybe for the time being we could just put the material so far in a section titled approproately, and then have another section with the other examples. Of course if it becomes too long, we should probably split the page.
But just one remark, concerning “classical” Tannaka duality: the original statement by Tannaka (and Krein, I gather) were about the simple case of a plain group and its linear representation category. No?
-
- CommentRowNumber30.
- CommentAuthorMike Shulman
- CommentTimeMay 16th 2010
I’m not really following this whole discussion, but I think perhaps Daniel Schaeppi’s paper should be mentioned as well in a categorical discussion of Tannaka duality?
-
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
Thanks, Mike!
I added the reference to the entry. But I am inclined to add also the following remark, after you or Todd give me a sanity check:
it seeems to me that the result about Tannaka duality for coalgebras, which is attributed to Deligne and Joyal-Street recalled by Schäppi on p. 2 is just another immedite consequence/special case of the general statement that we are claiming is just the Yoneda lemma:
recalll, the statement is that for an enriching category, a monoid in , the -enriched category of interval -modules and the forgetful functor, we have a natural isomorphism
in , where is computed in the enriched functor category. The claim is that this is nothing but the enriched Yoneda lemma in slight disguise.
Now, for the case of coalgebras we have , I suppose. Then as a special case we get that a coalgebra is equivalent to the end
computed in , which is the coend
In . This is the statement that Schäppi recalls on p. 2.
Right?
I am now inclined to say the following, but maybe I am overlooking something: since all this, as we have shown, is nothing but the enriched Yoneda lemma in slight disguise, it is clear that statements like this generalize to whatever context the enriched Yoneda lemma generalizes to. In particular I suppose when we enrich in/over a cosmos.
Is that maybe what’s going on in Schäppi’s article, secretly? (Haven’t had a time to read it jet.)
-
- CommentRowNumber32.
- CommentAuthorUrs
- CommentTimeMay 16th 2010
I might be hallucinating (in which case somebody please correct me) and still haven’t really read Joyal-Street in sufficient detail.
But given Schäppi’s lightning summary of the coalgebra result, I seem to be claiming that proposition 5 in Joyal-Street is a simple consequence of the enriched Yoneda lemma.
I have now made that claim a section Tannaka duality for coalgebras at Tannaka duality. It has been a hectic weekend with other distractions, and if I am overlooking something obviouss here I apologize for creating confusion. But maybe there is something of interest here. Would be grateful for a sanity check by somebody.
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeMay 16th 2010
- (edited May 16th 2010)
Ah, wait, now I see, I am being too simple-minded about the monoidal structure on . Um, need to think. But also have to go offline now…
-
- CommentRowNumber34.
- CommentAuthorMike Shulman
- CommentTimeMay 17th 2010
I invited Daniel Schaeppi to comment. He was unable to post himself due to captcha errors, but he sent me the reply below to post for him.
Mike pointed me to this thread; I have not yet had the time to study the Tannaka duality page on the nLab carefully, but one aspect of the theory seems to be missing so far.
It is my impression that one key ingredient of this whole theory is the interplay between finite dimensional representations and infinite dimensional algebras/coalgebras. To me it seems almost like a tautology to say that an algebra can be reconstructed from the category of all its modules, because the algebra is in particular a module over itself. If you keep track of the forgetful functor, this module can be characterized by a universal property, so it should not be surprising that the algebra can be reconstructed from the category of all modules. (Maybe this observation coincides with what you summarize as "Tannaka duality is just the Yoneda lemma".)
The theory of Tannakian categories concerns the relationship between affine group schemes/affine groupoids and their finite dimensional representations. These correspond to Hopf algebras and Hopf algebroids in the dual picture, and finite dimensional representations correspond to finite dimensional comodules. However, the Hopf algebra/Hopf algebroid is usually infinite dimensional already in the simplest examples (e.g. in the case of the additive and multiplicative group of the base field). The reconstruction theorem tells you that a Hopf algebra can be reconstructed from its finite dimensional comodules even if it is not itself finite dimensional. This is not just a formal consequence of the Yoneda lemma (there are cosmoi where the corresponding statement is false). To my knowledge the corresponding question is open even if you only replace the base field by a general commutative ring (and "finite dimensional" by "finitely generated projective").
Daniel Schäppi
-
- CommentRowNumber35.
- CommentAuthorMike Shulman
- CommentTimeMay 17th 2010
FWIW, Daniel’s comments are in line with what I suspected. In his paper, the Tannakian adjunction is obtained as a composite of two partial adjunctions. The first one is the semantics-structure adjunction, which I think is where the “tautology/Yoneda lemma” business goes on; he phrases it as a version of the formal theory of monads (which I quite like). The meat is in what happens when you compose with another adjunction, whose effect is to restrict to the category of “finite-dimensional” (or more generally, dualizable) things.
-
- CommentRowNumber36.
- CommentAuthorUrs
- CommentTimeMay 17th 2010
I see, thanks. That’s actually what Todd said above in #26.
Okay, I added remarks to the entry to make clear that the simple Yoneda-argument captures only a part of the story.
Could there maybe be a general statement for the case that the (co)algebra is a pro-object in , while its modules are taken just in ?
-
- CommentRowNumber37.
- CommentAuthorzskoda
- CommentTimeMay 17th 2010
- (edited May 17th 2010)
Are we the first to have observed that Tannaka duality is nothing but the Yoneda lemma? If not, where is this mentioned in the literature?
If you look at the old entry reconstruction theorem, I wrote there that all reconstruction theorems like Barr embedding theorem, Tannaka theorem, Krein theorem, Ulrich’s theorem, Giraud’s theorem boil down to Yoneda arguments, and this is well known.
Adjoint pair analysis of Galois theory is in the basis of categorical Galois theory of Janelidze which went to the bottom of the things.
-
- CommentRowNumber38.
- CommentAuthorzskoda
- CommentTimeMay 17th 2010
For 31: the things are not that simple. For exmaple, in algebraic context it is crucial that we work over a field. It is difficult to get Tannaka theorems over more general rings, one of the rare exceptions is Nori’s Tannakaina theorem (for references see motive). For coalgebraic/coend point of view I again recommend lectures of Pareigis.
-
- CommentRowNumber39.
- CommentAuthorzskoda
- CommentTimeMay 17th 2010
- (edited Jun 5th 2011)
the original statement by Tannaka (and Krein, I gather) were about the simple case of a plain group and its linear representation category
No. Tannaka’s reconstruction in general is all kinds of things, while Tannaka’s theorem and Krein’s theorem are two different particular theorems in functional analysis setup. So Krein theorem is not the same as Tannaka theorem. Both are special cases of many generalization. In modern generalizations one should also distinguish neutral and mixed Tannakian reconstruction, in first one looks at one fiber functor while in another one looks at a more stacky picture where one has fiber functors to a family of categories which correspond to something like algebraically closed extensions of the ground field. This leads to gerbes.
Edit: 1. slight correction: classical Tannaka and Krein theorems for compact topological groups are equivalent though differently formulated. Now we have a stub Tannaka-Krein theorem waiting for context. 2. It would be nice to eventually have the mixed Tannaka duality treated in Lab.
-
- CommentRowNumber40.
- CommentAuthorUrs
- CommentTimeMay 17th 2010
all reconstruction theorems like Barr embedding theorem, Tannaka theorem, Krein theorem, Ulrich’s theorem, Giraud’s theorem boil down to Yoneda arguments, and this is well known.
Where is this discussed explicitly?
-
- CommentRowNumber41.
- CommentAuthorDavid_Corfield
- CommentTimeMay 17th 2010
Is any interest being shown in the idea that alongside comodules people should look at contramodules?
-
- CommentRowNumber42.
- CommentAuthorzskoda
- CommentTimeMay 17th 2010
Where is this discussed explicitly?
I know no coherent treatment in this generality. It is being remarked here and there and some people who discovered some new generalizations like Rosenberg know it in various depth levels.
-
- CommentRowNumber43.
- CommentAuthorUrs
- CommentTimeMay 17th 2010
I know no coherent treatment in this generality.
Okay, if you come across anything, let me know.
Maybe it is common knowledge, but to me the two simple statements we have worked out here give me a much clearer picture of what is going on with Tannaka duality than I got from looking at the literature:
for unrestricted representations, Tannaka duality is a tautology , the enriched Yoneda lemma in slight disguise, ( any enriching category/cosmos)
so the crucial point is that some ends
over the category of all modules are already computed when restricting to just dualizable modules
To me, personally, this is a useful insight that helps me put Tannaka duality in perspective. If this is mentioned explicitly in the literature anywhere, I’d be interested.
-
- CommentRowNumber44.
- CommentAuthorMike Shulman
- CommentTimeMay 17th 2010
I got that same insight myself when I first read Daniel’s paper, although he phrases the first point a bit differently. Is his description explicit enough for you?
-
- CommentRowNumber45.
- CommentAuthorUrs
- CommentTimeMay 17th 2010
Is his description explicit enough for you?
Okay, I spent some time with the article now. I see it now.
More on this should be put in the nLab entry, but I am afraid I won’t have the time to do it.
-
- CommentRowNumber46.
- CommentAuthorzskoda
- CommentTimeJun 4th 2011
I have added numerous references and links to Tannaka duality. Many other microscopic changes.
-
- CommentRowNumber47.
- CommentAuthorzskoda
- CommentTimeJun 4th 2011
- (edited Jun 4th 2011)
I also created a separate entry for Tannaka-Krein theorem, that is the original Tannaka-type duality for compact topological groups; edits to Tadao Tannaka.
-
- CommentRowNumber48.
- CommentAuthorzskoda
- CommentTimeJun 5th 2011
- (edited Jun 5th 2011)
I think I should further change the idea section of Tannaka duality. I mean the way it is stated it applies to more general reconstruction theorems (for which we have the entry reconstruction theorem): we should add that we mean exclusively for categories of representations which are monoidal! Now, there is an interesting search for better understanding in recent work of Kornél Szlachányi (see arXiv/0907.1578 and the category list question here; he also has some new results I was told which are yet not on the arXiv). He points out the role of flat functors and the Grothendieck topology interpretation; everything would be trivial monadic nonsense if there were not the problem of the monoidal structure.
-
- CommentRowNumber49.
- CommentAuthorUrs
- CommentTimeJun 5th 2011
If you change it, please move the relevant bits to “reconstruction theorem”.
But maybe it would be easier to have it all discussed in one entry?
-
- CommentRowNumber50.
- CommentAuthorzskoda
- CommentTimeJun 5th 2011
Urs, the entry is already now scrolling over 8-9 pages in my window and it has still only formal content, what is small part of the story. Even if one restrains to algebraic case, as the original idea stated, the proofs have only group part so far and none on gerbes, coalgebras, Hopf algebroids and so on. It is a huge subject and I am thinking of further splittings; that is why I created a separate stub for Tannaka-Krein theorem in the narrow (classical) sense, that is for compact topological groups. One can not simultaneously discuss all the levels in reasonable length. Maybe you suggest the intermediate level, but I do not see it clearly. I mean Tannakian level is about representation categories which are monoidal and usually also rigid; one can consider some more general rep. categories without monoidal structure but then the reconstruction is very different, finally there are reconstruction theorems for categories of qcoh modules and so on and of sites, embedding theorems like that of Barr, Giraud etc. which are properly in reconstruction theorem of general type.
I have made numerous new references and links to bialgebroid, Hopf monad and Hopf algebroid.
-
- CommentRowNumber51.
- CommentAuthorzskoda
- CommentTimeJun 5th 2011
I added stub fiber functor for easy reference. Please improve.
-
- CommentRowNumber52.
- CommentAuthorzskoda
- CommentTimeJun 5th 2011
More about the general theme (of non-Tannakian) reconstruction: new entry Barr embedding theorem. Several person entries quoted at reconstruction, including Grigory Garkusha, Paul Balmer etc.
-
- CommentRowNumber53.
- CommentAuthorzskoda
- CommentTimeApr 18th 2013
- (edited Apr 18th 2013)
Are there some internal Tannaka theorems and even internal reconstruction theorems in general (internal in the sense of internal category theory), e.g. things like Barr embedding theorem, Giraud’s theorem, Freyd-Mitchell etc in internal setup ? For Tannaka, I mean, consider some class of Grothendieck 1-topoi, and internal monoidal categories there and try to realize them as internal representations of something in such a topos. I am pondering how to proceed in going toward certain statement in model theory which is in fact about internal 2-categories in certain presheaf category; but I see that I am not clear about how to internalize reconstruction reasoning (I can kind of formulate the expected statements but lack the logic of the proofs).
-
- CommentRowNumber54.
- CommentAuthorzskoda
- CommentTimeSep 5th 2013
I added
- J.P.Pridham, Tannaka duality for enhanced triangulated categories, arxiv/1309.0637
to the references at Tannaka duality. It is about Tannaka duality for dg-categories.
-
- CommentRowNumber55.
- CommentAuthorUrs
- CommentTimeOct 9th 2018
-
- CommentRowNumber56.
- CommentAuthornLab edit announcer
- CommentTimeApr 12th 2021
-
- CommentRowNumber57.
- CommentAuthorDELETED_USER_2018
- CommentTimeOct 5th 2021
- (edited Apr 11th 2023)
[deleted]
-
- CommentRowNumber58.
- CommentAuthorDmitri Pavlov
- CommentTimeOct 5th 2021
Re #57: The limit is not small, but it exists for locally λ-presentable V. The easiest way may be to argue that the end may be computed on the subcategory of λ-presentable objects, which is essentially small.
-
- CommentRowNumber59.
- CommentAuthorDELETED_USER_2018
- CommentTimeOct 7th 2021
- (edited Apr 11th 2023)
[deleted]
-
- CommentRowNumber60.
- CommentAuthorDmitri Pavlov
- CommentTimeOct 8th 2021
Come to think of it again, we may not need such a restriction in the first place.
Here is an argument that should prove the strong Yoneda lemma for arbitrary large enriched categories.
We have to show that the map
V^C(hom_C(c,-), F) → F(c)
is an isomorphism. In particular, we must show that the left side exists.
If the left side exists, it satisfies the universal property for ends. Pick an arbitrary object v∈V and apply the functor hom(v,-). Here hom(v,v’) denotes the set of maps from v to v’.
We get V^C(hom_C(c,-), F) = ∫_x V(hom_C(c,x), F(X)), so applying the functor hom(v,-) yields
∫_x hom(hom_C(c,x), F^v(x)),
where F^v(x) = hom_V(v,F(x)).
Now, as long as this functor is well-defined (meaning the end exists in the category of sets) and representable (as a functor of v), then the original end exists.
To show that it is well-defined and representable, we invoke the weak enriched Yoneda lemma for locally small categories. We get
∫_x hom(hom_C(c,x), F^v(x)) ≅ F^v(c).
This isomorphism is natural v. Thus, we proved that the above functor is well-defined and isomorphic to a representable functor. Thus, the strong Yoneda lemma holds for large enriched categories.
-
- CommentRowNumber61.
- CommentAuthorUrs
- CommentTimeOct 8th 2021
Am occupied elsewhere, but just to note that this thread started out, 11 years ago, with chat on just this kind of size issue (comments #1, #2, #7 etc.). But maybe this was never recorded properly in the entry. If you feel you could add it, please do.
-
- CommentRowNumber62.
- CommentAuthorjesuslop
- CommentTimeMar 30th 2023
-
- CommentRowNumber63.
- CommentAuthorDmitri Pavlov
- CommentTimeDec 10th 2023
Added:
- Nobuhiko Tatsuuma, Duality theorem for locally compact groups and some related topics, Algèbres d’opérateurs et leurs applications en physique mathématique (Proc. Colloq., Marseille, 1977), 387–408. Colloq. Internat. CNRS, 274, Éditions du Centre National de la Recherche Scientifique (CNRS), Paris, 1979. ISBN: 2-222-02441-2.
-
- CommentRowNumber64.
- CommentAuthorperezl.alonso
- CommentTimeMay 7th 2024
pointer
- Lukas Rollier. Equivariant Tannaka-Krein reconstruction and quantum automorphism groups of discrete structures (2024). (arXiv:2405.03364).
1 to 64 of 64