nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 17th 2010
I rephrased and restructured the Definition-section at join of simplicial sets a bit, in an attempt to make the exposition clearer. Please check if I succeeded.
-
- CommentRowNumber2.
- CommentAuthorTim_Porter
- CommentTimeFeb 17th 2010
I think that it is simpler to introduce ordinal sum directly. Don't confuse the picture with sum of cardinalities.
I am not sure I like the discussion of ordinals themselves at the entry ordinal number. The finite ordinals are much simpler than this! If we took two simple finite linear posets and formed their ordinal sum, that would be useful. My preference is for something like: ${0\lt 1\lt \ldots\lt p} \oplus {0^\prime\lt 1^\prime\lt \ldots\lt q^\prime} = \lt 1\lt \ldots\lt p\lt 0^\prime\lt 1^\prime\lt \ldots\lt q^\prime}\cong {0\lt 1\lt \ldots\lt p+ q + 1}$ with a brief explanation of notation, i.e. the primes are there to tell the difference between, for instance, 2 in the first set and 2 in the second. Underlines could equally well be used, or colours.
It is also useful to point out that the empty ordinal is needed so as to get the unit of the monoidal structure.
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeFeb 17th 2010
Don't confuse the picture with sum of cardinalities.
Sorry, what is wrong about what I said? Maybe I am mixed up.
-
- CommentRowNumber4.
- CommentAuthorTim_Porter
- CommentTimeFeb 18th 2010
I am naive enough to think that somehow ordinals are, sort of, categorified cardinals. What you say is not wrong as such it is just that to me it does not help. Understanding in ordinal sum of course means you have to think about the effect on the cardinality of the ordinals but putting that first seems to me to miss out on the simple geometric picture of putting one linearly order set before another. That is my only point. It is a pedagogic one not a mathematical one.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeFeb 18th 2010
Okay, how should we phrase this, then?. All I mean to tell the reader is that the monoidal structure on
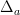 is just ordinary addition of natural numbers if we count not
is just ordinary addition of natural numbers if we count not ![\emptyset = [-1] \emptyset = [-1]](/extensions/vLaTeX/cache/latex_7c5de20dc95b9e5d857e67af1c5960e6.png) ,
, ![* = [0] * = [0]](/extensions/vLaTeX/cache/latex_d5de847172c6ddaf9666598c79032aaf.png) but count
but count ![\emptyset = [0] \emptyset = [0]](/extensions/vLaTeX/cache/latex_b555cd7f86e99598a4014ad42c65bf8a.png) ,
, ![* = [1] * = [1]](/extensions/vLaTeX/cache/latex_c454ee2919023106d66fc05756d33610.png) , etc.
, etc. -
- CommentRowNumber6.
- CommentAuthorTim_Porter
- CommentTimeFeb 18th 2010
Perhaps??? I still feel that the ordinary arithmetic in $\marthbb{N}$ is really a
red herring'. It de-emphasises the order structure and therefore the categorical and geometric structures. The way that the operation is going to be used is geometric and categorical not arithmetic. The arithmetic aspect is a side effect. Because of that I would put a simple example early, with a fairlygraphic' description and then put your idea immediately after as a `note : to some extent we can think of this operation as being ....' with your comment.I will try to put a revision on the entry and see how that looks, but Thursday is a busy day so it won't be immediately.
-
- CommentRowNumber7.
- CommentAuthorHarry Gindi
- CommentTimeFeb 18th 2010
- (edited Feb 18th 2010)
I think it might be useful to give some examples of how to compute a join. Is anyone opposed to me doing so?
-
- CommentRowNumber8.
- CommentAuthorTim_Porter
- CommentTimeFeb 18th 2010
OOPS wrong ' !
-
- CommentRowNumber9.
- CommentAuthorTim_Porter
- CommentTimeFeb 18th 2010
@Harry It depends on what you think 'compute' means! There are some examples in my paper with Phil Ehlers that might be useful.
-
- CommentRowNumber10.
- CommentAuthorHarry Gindi
- CommentTimeFeb 18th 2010
- (edited Feb 18th 2010)
Computing the join standard simplices is easy, but computing say, the join of a simplex and a horn is not nearly as intuitive.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeFeb 18th 2010
- (edited Feb 18th 2010)
Is anyone opposed to me doing so?
On the contrary. I am opposed to you not doing so.
Please do!
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeFeb 18th 2010
- (edited Feb 18th 2010)
Tim,
to understand the monoidal structure on objects we use addition of cardinalities,
to understand it on morphisms we remember that underlying this is ordinal addition.
Do you agree? I am not saying that the ordinal aspect is not crucial here. All I want to do is tell the reader in the introductory part at the beginning that the funny addition rule
![[n] + [m] = [n+m+1] [n] + [m] = [n+m+1]](/extensions/vLaTeX/cache/latex_743335c30f99f666b6840a7855a12200.png) is just ordinary addition of natural numbers, only that they are all off by one.
is just ordinary addition of natural numbers, only that they are all off by one.I think this is a very simple statement that deserves to be stated in the "Idea"-seciton. That doesn't prevent an in-depth discussion of ordinal addition to follow.
-
- CommentRowNumber13.
- CommentAuthorTim_Porter
- CommentTimeFeb 18th 2010
I think that if someone had said to me that, when I was a student, I would have thought 'attention fudge coming'! I think the problem is exactly that you are thinking of the objects as cardinals. I am thinking of them as linear partially ordered sets. The addition rule is not then `funny', because the ordinal (topologists' version of simplex) [n] has itself n+1 elements when we forget the order. The addition of cardinals then reflects the usual union structure when we forget the orders. The rule [n} + [m] = [n+m+1] misleading I think.If you said is just union of sets, I would be more inclined to agree.
I will have a go and see if I can get a compromise wording for the ideas section, and then we can continue our pedagogic debate if it does not work!
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeFeb 18th 2010
The addition rule is not then `funny', because the ordinal (topologists' version of simplex) [n] has itself n+1 elements when we forget the order. The addition of cardinals then reflects the usual union structure when we forget the orders.
This seems to be precisely what I have been saying.
If you said is just union of sets, I would be more inclined to agree.
But under cardinality, union of sets maps to addition of cardinalities. And the little symbol "
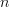 " as in
" as in 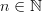 is a symbol for cardinalities.
is a symbol for cardinalities.So I am not sure what our disagreement is. Maybe it is just that my wording is bad?
-
- CommentRowNumber15.
- CommentAuthorTim_Porter
- CommentTimeFeb 18th 2010
The changes are not in the ideas section, but I hope they do what was suggested.
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeFeb 18th 2010
Very nice. I like that. Thanks, Tim!!
-
- CommentRowNumber17.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 18th 2010
In response to Harry, I added the example of the join of a horn and a simplex (incidentally illustrating the Day convolution point of view). Also added some words to Idea. -
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeFeb 18th 2010
Thanks, Todd. I moved that to a special Examples-section, so that readers can spot it more easily.
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeMar 17th 2010
- (edited Mar 17th 2010)
started a section with simple examples for cones (join with the point) at join of simplicial sets.
By the way: the first formula that is currently given in the section Examples looks wrong to me. .I seem to remember that Todd wrote this and I guess I must be missing something: it says
![\Lambda_k[m] \star \Delta[n] \simeq \Lambda_k[m+n+1] \Lambda_k[m] \star \Delta[n] \simeq \Lambda_k[m+n+1]](/extensions/vLaTeX/cache/latex_41cc39fc1919389c330b127c4c4e3ba9.png)
But setting
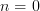 this does not reproduce for instance the simple cone examples now listed there. Am I mixed up?
this does not reproduce for instance the simple cone examples now listed there. Am I mixed up? -
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeMar 17th 2010
- (edited Mar 17th 2010)
Added another Example-section paragraph on simplicial spheres to join of simplicial sets.
I am still looking for some reference that would discuss examples of joins at greater length than Ehlers/Porter or Joyal or Lurie. Is there any?
-
- CommentRowNumber21.
- CommentAuthorHarry Gindi
- CommentTimeMar 17th 2010
- (edited Mar 17th 2010)
Does anyone else think that the picture in that article is gigantic and silly looking? I'm going to make a more appropriate one in the SVG editor right now.
-
- CommentRowNumber22.
- CommentAuthorHarry Gindi
- CommentTimeMar 17th 2010
- (edited Mar 18th 2010)
Okay, done. Now look at those diagrams over at join of simplicial sets! I got rid of that gaudy awful one from wikipedia. Math does not come in red and blue, it comes in shades of grey! By the way, it seems like it would be a lot better if the .svg files got saved to the nLab server, since the edit page is getting hard to read after only two diagrams. It seems like all you would need to do is write something like #include file.svg. This should be fine, since SVG files are so small.
I do wonder whether putting the giant
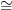 is really appropriate, since they're formally equal (I just reoriented the picture), but hey, it seemed like it worked with the nPOV.
is really appropriate, since they're formally equal (I just reoriented the picture), but hey, it seemed like it worked with the nPOV. -
- CommentRowNumber23.
- CommentAuthorHarry Gindi
- CommentTimeMar 18th 2010
- (edited Mar 18th 2010)
<p>Also, the statement about the join of a simplex and a horn is just plain false. Consider any 2-horn <img src="/extensions/vLaTeX/cache/latex_8c5de91f1632bc8ea9052cd62552b855.png" title="\Lambda^n_{k}" style="vertical-align:-20%;" class="tex" alt="\Lambda^n_{k}" />. Taking the cone gives us two faces. This is easy to see as:</p> <p>2-horn: <img src="/extensions/vLaTeX/cache/latex_31fbcedb30c9b53675f1d21805c5486f.png" title="0\to 1\to 2" style="vertical-align:-20%;" class="tex" alt="0\to 1\to 2" /></p> <p>cone over the 2-horn:</p> <img src="/extensions/vLaTeX/cache/latex_a81eeac5e7bccbf04b58674685453124.png" title="\begin{matrix}&&c&&\\ &\swarrow&\downarrow&\searrow&\\ 0&\to&1&\to&2 \end{matrix}" style="vertical-align:-20%;" class="tex" alt="\begin{matrix}&&c&&\\ &\swarrow&\downarrow&\searrow&\\ 0&\to&1&\to&2 \end{matrix}" /> <p>Which is not a 3-horn.</p> -
- CommentRowNumber24.
- CommentAuthorDavidRoberts
- CommentTimeMar 18th 2010
The first picture is a bit broken: the two labels have missing closing square brackets, and are intersecting the left simplex. You probably know already, but it took me a bit to realise that the labels weren't meant to be sub-things of the left object.
-
- CommentRowNumber25.
- CommentAuthorHarry Gindi
- CommentTimeMar 18th 2010
- (edited Mar 18th 2010)
Could you explain a little more what you mean?
Also, even if they're not great, they're better than that awful picture we had there.
Edit: I see what you mean. For some reason the editor bugged and broke how it was supposed to be. I'll fix it in a second.
-
- CommentRowNumber26.
- CommentAuthorDavidRoberts
- CommentTimeMar 18th 2010
- (edited Mar 18th 2010)
The labels are [0]*[2 and [2]*[0 at present. I hesitate to fiddle with the source, else I'd fix it myself. The labels are placed (at least in my browser) over two of the vertical lines in the left picture, making it look like they are labelling those lines, and not the two pictures.
And yes, they are far superior to the old picture. Thanks for whipping them up :)
edit: cross-over there on comments -
- CommentRowNumber27.
- CommentAuthorHarry Gindi
- CommentTimeMar 18th 2010
Fixed. The iTex integration appears to be kinda broken, so I've given up on using it.
-
- CommentRowNumber28.
- CommentAuthorUrs
- CommentTimeMar 18th 2010
Also, the statement about the join of a simplex and a horn is just plain false.
Yes, that's what I said above. And your example is already worked into the entry.
But I wonder what Todd had in mind here...
-
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeMar 18th 2010
Harry,
thanks for the nice pictures!!
-
- CommentRowNumber30.
- CommentAuthorHarry Gindi
- CommentTimeMar 18th 2010
Yes, that's what I said above. And your example is already worked into the entry.
Oops! That's what I get for a.) not reading the discussion and b.) not reading the whole article.
-
- CommentRowNumber31.
- CommentAuthorUrs
- CommentTimeMar 18th 2010
No problem. But hopefully Todd show up here at some point. I suppose there was just some trivial typo in that formula which could easily be fixed. But I am not really sure yet.
-
- CommentRowNumber32.
- CommentAuthorHarry Gindi
- CommentTimeMar 18th 2010
- (edited Mar 18th 2010)
It cannot. I can prove the correct formula by induction, but it's a pain in the neck keeping the ordering straight when the join is on the left. Joining the simplex on the right is easier, because the order is preserved. Specifically, the join of a simplex
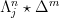 can be described as a simplicial subset of
can be described as a simplicial subset of 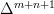 where given the unique nondegenerate
where given the unique nondegenerate 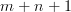 simplex
simplex  , the join is given by union of the following
, the join is given by union of the following 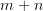 -simplices as:
-simplices as: 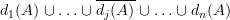 , where the overline denotes omission (we can write this as a pushout as well, which allows us to relate this to the definition). Computing the join on the left, you have to worry about keeping the indexing straight, but it's roughly the same idea.
, where the overline denotes omission (we can write this as a pushout as well, which allows us to relate this to the definition). Computing the join on the left, you have to worry about keeping the indexing straight, but it's roughly the same idea.To compute it on the left, I think you can just add n+1 to all of the coordinates.
-
- CommentRowNumber33.
- CommentAuthorUrs
- CommentTimeMar 18th 2010
If you have worked computations, you should put them into the nLab entry in the Examples-section.
-
- CommentRowNumber34.
- CommentAuthorHarry Gindi
- CommentTimeMar 18th 2010
- (edited Mar 18th 2010)
How do we induce the face/degeneracy maps on the join? I'm having a hard time doing it from the definition.
Oh wait, I think I've got it.
Edit: Nope
-
- CommentRowNumber35.
- CommentAuthorHarry Gindi
- CommentTimeMar 18th 2010
- (edited Mar 18th 2010)
Alright, so actually giving a construction of the face and degeneracy maps on the join of two simplicial sets is not immediately clear. Presumably we have to induce them from the two things we're joining, but when trying to actually give them, you run into something of a combinatorial problem, unless I'm doing it wrong. To actually prove the above statement using the definition, it seems like you need to know exactly what these maps are (Lurie mysteriously leaves them out).
Edit: I remembered that a while ago, Emily Riehl answered one of my MO questions with a relevant answer. She gives the formulas there. I'll add them to the nLab at some point either later or tomorrow.
-
- CommentRowNumber36.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
I'll add them to the nLab at some point either later or tomorrow.
Try to procastinate your procastination.
Here it is..
-
- CommentRowNumber37.
- CommentAuthorHarry Gindi
- CommentTimeMar 19th 2010
Can we induce these by universal properties or no shot?
-
- CommentRowNumber38.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2010
@Harry Try to get hold of Ehlers-Porter (or ask me if you cannot get it) or better Phil Ehlers' thesis (for which you will need to ask me as it has not been put on the Bangor link). All the formulae are clear if you look at the coend (?) form of the expression BUT you do need to work it through for augmented simplicial sets. (I have not checked if it is a coend or an end formula I should remember :-(! but don't.) There is no combinatorial problem really, you need to understand the ordinal sum and to analyse various maps involving that.
-
- CommentRowNumber39.
- CommentAuthorEric
- CommentTimeMar 19th 2010
I'd be interested in a copy of the thesis if possible...
-
- CommentRowNumber40.
- CommentAuthorHarry Gindi
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
@Tim: I'm buying it as soon as the semester ends April 30 (or as soon as I get home). The problem that I'm running into is inducing the maps by the universal property by hand and showing what they are explicitly, which feels very combinatorial.
Two questions:
Is there a difference between asSet and ASSet?
Is the coend formula on the page:
![(S \star S')_n:= \int^{[i],[j] \in \Delta_a} S_i \times S'_j \cdot \Delta([n],[i] \star [j]) (S \star S')_n:= \int^{[i],[j] \in \Delta_a} S_i \times S'_j \cdot \Delta([n],[i] \star [j])](/extensions/vLaTeX/cache/latex_5d11c828c81b970e3ba2fb1d72c2d872.png)
the same thing as:
![(S \star S')_n := \int^{[i],[j] \in \Delta_a} S_i \times S'_j \times \Delta_a([n],[i] \star [j]) (S \star S')_n := \int^{[i],[j] \in \Delta_a} S_i \times S'_j \times \Delta_a([n],[i] \star [j])](/extensions/vLaTeX/cache/latex_1473710856ed75d3688945a73eee0f42.png) ?
?The actual question is about the second
 instead of a cdot and with the Hom in
instead of a cdot and with the Hom in 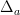 rather than
rather than 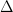 . If not, what does the cdot mean, and why are we only taking homs in
. If not, what does the cdot mean, and why are we only taking homs in 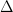 ? (Note: The notation I used here was just to bring it in line with the defintion of the day convolution used elsewhere). Anyway, it still isn't obvious to me how to induce the the face and degeneracy maps relative to the original ones.
? (Note: The notation I used here was just to bring it in line with the defintion of the day convolution used elsewhere). Anyway, it still isn't obvious to me how to induce the the face and degeneracy maps relative to the original ones. -
- CommentRowNumber41.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
@Harry Do you what a pdf file of the thesis, warts and all? (Like almost any thesis!) What page? You say that page but ... I will look!
It does not seem to be defined> Referring to Phil's thesis
`Note that for X ? ob(Sets) and Y ? ob(C ), for some category C , the X -indexed copower of Y shall be denoted by X · Y (if it exists).'
It is therefore isomorphic to what you say, but I would use 'or' or \oplus instead of star as that structure is the ordinal sum.
The point that is worth looking at to gain experience in handling the join is the structure of Hom([n],[i]\star[j]) for different values of the various bits. I listed the low dimensional cases to see what was happening and how they varied with i and j and that mad a lot of sense later on. (I do something related to this in some part of the Menagerie but I am looking at the subdivision rather than the join so I will not suggest your looking there yet.)
-
- CommentRowNumber42.
- CommentAuthorHarry Gindi
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
I meant the nLab page. I've clarified my post. Thanks for the help, by the way.
Reading your post again, why would
![\Delta([n],[i]\star [j]) \Delta([n],[i]\star [j])](/extensions/vLaTeX/cache/latex_52df75b694097c69ba3d51610498ff7c.png) be an object of
be an object of 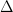 ? Isn't it just a set, or is that some kind of internal hom?
? Isn't it just a set, or is that some kind of internal hom?The thing is, I understand what's going on geometrically in the easy cases, but the definition is really hard to work with for me for some reason. I can even visualize what's going on at each n, but that only helps me deal with the nondegenerate simplices.
Edit: Also, yes, I would like to see the thesis.
Edit 2: I think I see what you're saying about the indexed copower thing, but it doesn't apply in the notation used on the page. In this notation, notice that
![\Delta([n],[i] \star [j]) \Delta([n],[i] \star [j])](/extensions/vLaTeX/cache/latex_216271e34e114aaac17d853663932fff.png) is actually a set, so we can define it as:
is actually a set, so we can define it as:![(S \star S')_n:= \int^{[i],[j] \in \Delta_a} S_i \times S'_j \times \Delta([n],[i] \star [j]). (S \star S')_n:= \int^{[i],[j] \in \Delta_a} S_i \times S'_j \times \Delta([n],[i] \star [j]).](/extensions/vLaTeX/cache/latex_57975657c97d5c349a1041cfc339d905.png)
However, we would need to use the indexed copower notation in the following notation:
![(S \star S')(-):= \int^{[i],[j] \in \Delta_a} S_i \times S'_j \cdot \Delta(-,[i] \star [j]). (S \star S')(-):= \int^{[i],[j] \in \Delta_a} S_i \times S'_j \cdot \Delta(-,[i] \star [j]).](/extensions/vLaTeX/cache/latex_0c0e52e7026ca17f79f6658dfe89a760.png)
Because the thing on the right is a presheaf, not actually a set.
Edit 3: I see you've already responded.
-
- CommentRowNumber43.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
@Harry My confusion sorry. I also went to eat my breakfast in between doing an edit and confirming it. The term IS just a set , but in the paper that term is written as
![\Delta([i]\oplus[j]) \Delta([i]\oplus[j])](/extensions/vLaTeX/cache/latex_ffb2702e6ed2f67ac66d2e6b22bd65e3.png) or something like that so the variation in [n] is within the notation.
or something like that so the variation in [n] is within the notation.If I understand your problem it may be helped by looking at the ordinal sum in more detail. See what the variation in i and j is and in particcular how it interacts with the coend.
-
- CommentRowNumber44.
- CommentAuthorHarry Gindi
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
One last thing: is there any reason why we're taking the hom in
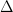 rather than
rather than 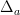 ? At least how that's defined there, it doesn't give us the definition of
? At least how that's defined there, it doesn't give us the definition of 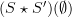 .
. -
- CommentRowNumber45.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2010
It should probably be in the augmented category. You're right.
-
- CommentRowNumber46.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
Is there a difference between asSet and ASSet?
I started changing the notation for
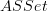 to
to 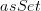 . Maybe a bad idea.
. Maybe a bad idea.Can't we simply link to the thesis or whatever there is from the nLab entry? Or is the link somehow required to remain secret?
-
- CommentRowNumber47.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2010
@Harry Can you send me an e-mail with your e-mail address as then my system will have your address available. I don't seem to have it.
-
- CommentRowNumber48.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
We can also upload the pdf to the nLab server and have it linked here!
-
- CommentRowNumber49.
- CommentAuthorHarry Gindi
- CommentTimeMar 19th 2010
- (edited Dec 16th 2018)
Meanwhile, I found good notation for the ordinal sum. I've changed the symbol to . This protects our direct sum symbol and also gives us a "sum that adds together two numbers in square brackets".
. This protects our direct sum symbol and also gives us a "sum that adds together two numbers in square brackets".
That is \boxplus, if you're trying to use it.
I tried to put the note about abuse of notation in a query box really quickly, but I think I might have just knocked Tim off of the page. -
- CommentRowNumber50.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2010
In fact I have made it available on the Lab page in the reference section.
My choice of \oplus was linked to the idea that plus is sum whilst the o reminds one of ordinal. There is probably little possibility of confusion with direct sum as that is more in algebraic contexts.
-
- CommentRowNumber51.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2010
I need to download the thesis again as it seems to be a binary file.not a pdf.
-
- CommentRowNumber52.
- CommentAuthorHarry Gindi
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
Well,
 is not used for anything either, and I like my idea that it's adding up numbers in square brackets. I think that actually the proper notation is
is not used for anything either, and I like my idea that it's adding up numbers in square brackets. I think that actually the proper notation is 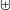 , which I think is the ordered union of totally ordered sets, but honestly, that's really no more than a guess.
, which I think is the ordered union of totally ordered sets, but honestly, that's really no more than a guess. -
- CommentRowNumber53.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2010
I would suggest that we have a new notion 'evil' when applied to comments. Really 'the proper notation' how could you? Do you mean that you saw it in some paper by someone in a position of power!!!!!! <-only joking. I quite like 'or' as it is simple.
I was trying to amend the link as I am getting a strange result from the link to the thesis.
-
- CommentRowNumber54.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
I have made it available on the Lab page in the reference section.
Thanks!!
-
- CommentRowNumber55.
- CommentAuthorEric
- CommentTimeMar 19th 2010
I have made it available on the Lab page in the reference section.
Yeah, thanks! :)
First impression... very nice and readable. Maybe I will actually be able to understand it :)
-
- CommentRowNumber56.
- CommentAuthorHarry Gindi
- CommentTimeMar 19th 2010
By the way, does the day convolution always take symmetric monoidal products to asymmetric ones, or is the join in the underlying category not actually symmetric?
-
- CommentRowNumber57.
- CommentAuthorHarry Gindi
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
Alright, I've just realized something... I think..
The structure maps of the join (face/degeneracy) must be taken as part of the definition if we define the join to be
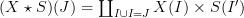
with the appropriate conditions I < I' and
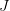 a finite nonempty totally ordered set.
a finite nonempty totally ordered set.This is because a priori, this does not define a functor, and it's almost definitely not true that there is only one functor with these sets of simplices.
When we define it using the Day convolution, we've already defined the underlying product, so the structure is immediate.
To reiterate,
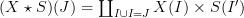
is not a definition of the join, just the definition of the set of n-simplices of the join! Without the structure maps, this is symmetric.
-
- CommentRowNumber58.
- CommentAuthorUrs
- CommentTimeMar 26th 2010
That's correct. If that wasn't clear before, try to make it clearer at the entry.
-
- CommentRowNumber59.
- CommentAuthorHarry Gindi
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
Damn it! It's been five months that I've been essentially stuck on that stupid definition.
Luuurieee!!!!
(Note: HTT does not define these maps in its definition of the join. This means that it is an error in HTT, especially because he does not give the Day convolution definition. If he had, it would be fine to leave the maps out.)
You can only leave the structure maps out of the definition if the object is defined by a universal property. =(
If you're sure that I'm right, I'm going to e-mail Lurie about this, but I'd like to make sure that I'm not mistaken before I do so. Can anyone else confirm that there is no way to induce the structure maps using the definition above by some sort of universal property?
-
- CommentRowNumber60.
- CommentAuthorUrs
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
Wait a second here. We are talking about the definition on p. 42 of HTT?
Hm, maybe the statement of the definition itself could be improved, but right after that it says what exactly the join of two simplices is in a way that does define the structure maps, and then there is the remark about how all other joins are obtained form this by colimits in sSet.
So the information is all there.
-
- CommentRowNumber61.
- CommentAuthorHarry Gindi
- CommentTimeMar 26th 2010
- (edited Mar 26th 2010)
He presents the maps
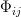 as something that he has derived, not as something that he has defined.
as something that he has derived, not as something that he has defined.In particular, even given this information, I don't see how you can derive the actual explicit maps.
-
- CommentRowNumber62.
- CommentAuthorUrs
- CommentTimeMar 26th 2010
You are right that the exposition of the statement is maybe suboptimal.
But it says explicitly what the joint of two simplices is. Including everything. Then it says that join preserves colimits. Every simplicial set
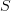 is the colimit over its simplices
is the colimit over its simplices![S = \int^{n} S_n \cdot \Delta[n] = colim_{n, S_n} \Delta[n] S = \int^{n} S_n \cdot \Delta[n] = colim_{n, S_n} \Delta[n]](/extensions/vLaTeX/cache/latex_c8336f13f51db6d4871b2fa23b0a7c8b.png) .
.Therefore we have for
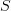 and
and 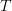 two simplicial sets, that their join is given by the colimit
two simplicial sets, that their join is given by the colimit![S \star T = (\int^n S_n \Delta[n]) \star (\int^k T_k \Delta[k]) \simeq \int^{n,k} S_n \times T_k \cdot (\Delta[n] \star \Delta[k]) S \star T = (\int^n S_n \Delta[n]) \star (\int^k T_k \Delta[k]) \simeq \int^{n,k} S_n \times T_k \cdot (\Delta[n] \star \Delta[k])](/extensions/vLaTeX/cache/latex_f056e7348f4d9516dc336c9b2fbe7885.png) .
.This is said there, even though not very explicitly.
-
- CommentRowNumber63.
- CommentAuthorHarry Gindi
- CommentTimeMar 27th 2010
Anyway, Tyler Lawson has spelled everything out over at this post on MO. This is probably the most complete exposition of the matter anywhere, given the number of papers that I've read that take it for granted. I'll edit the page accordingly later.
-
- CommentRowNumber64.
- CommentAuthorUrs
- CommentTimeMar 29th 2010
I'll edit the page accordingly later.
Please do!
-
- CommentRowNumber65.
- CommentAuthorTodd_Trimble
- CommentTimeApr 1st 2010
I've been away from the math blogosphere for a spell (just came back today), and I'm sifting through many, many comments. Yes, of course I wrote down something wrong for the join of a horn and a simplex, but hopefully the underlying idea was clear: it's that
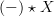 is cocontinuous and therefore preserves unions. A horn, as a subobject
is cocontinuous and therefore preserves unions. A horn, as a subobject ![\Lambda_k[m] \Lambda_k[m]](/extensions/vLaTeX/cache/latex_b27127ed6d3b88b8fb1c59ea42468745.png) of
of ![\Delta[m] \Delta[m]](/extensions/vLaTeX/cache/latex_15ee7899559146707b2014365d2606d4.png) is a union of
is a union of 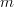 faces, i.e., inclusions of the form
faces, i.e., inclusions of the form ![i_j: \Delta[m-1] \to \Delta[m] i_j: \Delta[m-1] \to \Delta[m]](/extensions/vLaTeX/cache/latex_8f7d73882c854da2eec7c19ece3d6ac5.png) for
for 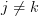 . So
. So ![\Lambda_k[m] \star \Delta[n] \hookrightarrow \Delta[m] \star \Delta[n] \Lambda_k[m] \star \Delta[n] \hookrightarrow \Delta[m] \star \Delta[n]](/extensions/vLaTeX/cache/latex_11b55fc8e42c2e01ab4df4194cbaabb0.png) is a union of
is a union of 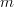 subobjects of the form
subobjects of the form![i_j \star id: \Delta[m-1] \star \Delta[n] \hookrightarrow \Delta[m] \star \Delta[n] i_j \star id: \Delta[m-1] \star \Delta[n] \hookrightarrow \Delta[m] \star \Delta[n]](/extensions/vLaTeX/cache/latex_0d3933186428c8f97d26d6da8bca0f3e.png)
or a union of
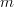 faces of the form
faces of the form ![\Delta[m+n] \hookrightarrow \Delta[m+n+1] \Delta[m+n] \hookrightarrow \Delta[m+n+1]](/extensions/vLaTeX/cache/latex_5615e2c888d15d38f852a500f91c872e.png) .
.When I wrote the incorrect formula, I was probably subvocalizing as follows: a horn is the union of all but one face, so when we join with a simplex, we again get a union of all but one face. In other words, I wasn't counting positively as I should have; I was counting negatively. It was a careless slip.
(Looking at what Harry wrote at #32, all this seems to have been sorted out already, but Urs at #31 asked me to explain what I was thinking. The larger point, that cocontinuity of Day convolution in each argument is useful in calculations, is still valid (-: .)
-
- CommentRowNumber66.
- CommentAuthorHarry Gindi
- CommentTimeApr 1st 2010
@Todd: It was suggested that I learn about the Trimble n-cat to do homotopy theory. Do you have a suggestion for reading about it, given that you're the man himself?
-
- CommentRowNumber67.
- CommentAuthorDavidRoberts
- CommentTimeApr 1st 2010
If I may interject, I would suggest reading a bit about operads before Trimble n-categories. But as a start, try Leinster's survey of definitions of n-categories, and then the nLab (obviously) and there is some stuff by Eugenia Cheng (and someone else, I think). -
- CommentRowNumber68.
- CommentAuthorTodd_Trimble
- CommentTimeApr 1st 2010
The 2004 notes by Eugenia Cheng and Aaron Lauda are very good (as are Tom's, but my memory is that Cheng-Lauda proceed at a more leisurely pace). Yes, you will need to know about operads, but you very well might already, and for which there is a ton of accounts -- my own first exposure to them was through reading Stasheff's seminal work on higher associativities and also J.P. May's Geometry of Iterated Loop Spaces, both of which I warmly recommend. What I wrote up on Trimble n-cats in the nLab is a slightly different approach, and the one I used in my original talk on the subject.
But I'm curious about that suggestion that you read up on this to "do homotopy theory", which sounds odd to my ears. Did someone write that down somewhere, so that can see the context where it was made?
-
- CommentRowNumber69.
- CommentAuthorHarry Gindi
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
No, I was talking to a graduate student at UIUC on IRC who suggested that to study homotopy groupoids rather than groups, I should learn at least one formalism for weak n-categories. He suggested that quasicategories are not optimal for this, because they're very hard to compute with.
-
- CommentRowNumber70.
- CommentAuthorTodd_Trimble
- CommentTimeApr 1st 2010
Oh, okay -- I guess you mean wrapping your head around
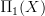 ,
, 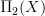 , and so on -- and understanding what operations are involved. It's certainly true that the problem of understanding that is what drove me to my definition, and it's a very good exercise. You might try banging your head for a while against that, and seeing what you come up with. Then you can check against what other people (myself included) came up with -- that might pack a greater punch than just reading about it straight away.
, and so on -- and understanding what operations are involved. It's certainly true that the problem of understanding that is what drove me to my definition, and it's a very good exercise. You might try banging your head for a while against that, and seeing what you come up with. Then you can check against what other people (myself included) came up with -- that might pack a greater punch than just reading about it straight away.It's also an interesting problem to try to whittle these big structures down to size by considering what their skeletons look like, more particularly how such skeletons are assembled from copies of
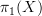 ,
, 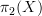 , etc. and operations between them. This leads quickly to things like k-invariants.
, etc. and operations between them. This leads quickly to things like k-invariants. -
- CommentRowNumber71.
- CommentAuthorHarry Gindi
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
I know nothing about based homotopy either! I mean, do you have any book suggestions for me to quickly get to all of this stuff with higher homotopy groupoids? I've heard that Tim Porter's book is good, but I'm broke at the moment, and I'm going to buy it over the summer. So until then, do you have any suggestions? I've looked at the beginning of Switzer, but everything he does is totally focused on based homotopy theory.
-
- CommentRowNumber72.
- CommentAuthorDavidRoberts
- CommentTimeApr 1st 2010
In that case, buy Ronnie Brown's book: it costs 5 pounds (USD 7.60) in electronic format - I have it and it is a very useful searchable resource. It only covers 1-dimensional homotopy groupoids, but it's a good intro to topology and the techniques of fundamental groupoids.
-
- CommentRowNumber73.
- CommentAuthorHarry Gindi
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
No no I'm quite familiar with the fundamental groupoid. I meant the higher homotopy groups.
The fundamental groupoid is pretty easy to understand.
I'll buy that book this week after I finish these exercises from milnor.
-
- CommentRowNumber74.
- CommentAuthorDavidRoberts
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
The action of
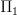 on the collection of
on the collection of 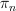 s at various basepoints is good to know. Then there are various operations among the homotopy groups (giving rise to what is called a
s at various basepoints is good to know. Then there are various operations among the homotopy groups (giving rise to what is called a 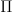 -algebra, see Blanc-Dwyer-Goerss in Topology in 2004). Other than that, they not too tricky. Going from groups to n-groupoids is of course the hard bit, unless you warm up via strict n-groupoids, say using crossed complexes. Then Ronnie Brown's book with Higgins and Severa on Nonabelian Algebraic Topology will come in handy. There's a lot of algebra there, but the main points should be extractable.
-algebra, see Blanc-Dwyer-Goerss in Topology in 2004). Other than that, they not too tricky. Going from groups to n-groupoids is of course the hard bit, unless you warm up via strict n-groupoids, say using crossed complexes. Then Ronnie Brown's book with Higgins and Severa on Nonabelian Algebraic Topology will come in handy. There's a lot of algebra there, but the main points should be extractable. -
- CommentRowNumber75.
- CommentAuthorHarry Gindi
- CommentTimeApr 1st 2010
I love algebra though!
-
- CommentRowNumber76.
- CommentAuthorTim_Porter
- CommentTimeApr 1st 2010
Which book by me? Ronnie's book is available from his website in draft form.
I keep on trying to get people to make the link between the various n-groupoids (non-strict) and the homotopy operations (Whitehead products etc.) They must correspond to various bits of non-strictness (e.g. some indications and intuitions of interchange / Gray tensor product related to lowest order Whitehead product, but I would like to see formulae (that were moderately simple).
David Blanc has lots of work on Pi algebras and it is tantalising both for what it says and does not say! He has a very recent preprint with Simona Paoli that is very interesting. It is available from her web page http://math.aa.psu.edu/~simona/index_file/Page290.htm (last in the list).
-
- CommentRowNumber77.
- CommentAuthorDavidRoberts
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
Presumably your book with Kamps. As I'm not sure what sort of homotopy theory this person Harry was talking to had in mind, I'm just suggesting the quick references that come to mind. I'm a bit nonplussed by Harry intently wanting to know about higher homotopy groups and seeming lost; as a formal object there's not much to them. Personally I think it's the operations that are more complicated and interesting, and the algebraic structres (crossed complexes, operations etc) that they form.
-
- CommentRowNumber78.
- CommentAuthorTim_Porter
- CommentTimeApr 1st 2010
Far be it for me to discourage buying that book, but I suspect the Menagerie (in one of its shorter versions, 10 chapters) would be sufficient for some of what Harry wants. Kamps - Porter is available in part on the web. Have a look at contents etc always before buying! We wrote that book as we felt there was a gap in the literature and the actual constuctible homotopies with cylinders that were functorial were all to often discarded as being non-fashionable compared with model categories.
-
- CommentRowNumber79.
- CommentAuthorHarry Gindi
- CommentTimeApr 1st 2010
- (edited Apr 1st 2010)
Wait, Kamps-Porter is available in an electronic version?
@David: I'm not confused about the higher homotopy groups. I mean that I've never studied/used them.
-
- CommentRowNumber80.
- CommentAuthorTim_Porter
- CommentTimeApr 1st 2010
No but a preview version is:
http://books.google.co.uk/books?id=7JYKxInRMdAC&printsec=frontcover&dq=Kamps+Porter&source=bl&ots=uuCkXpHhB5&sig=-S509JARITeXpXp9EtgXAGR3YDk&hl=en&ei=e2u0S8mtNNS04gaMtOjaDg&sa=X&oi=book_result&ct=result&resnum=5&ved=0CBIQ6AEwBA#v=onepage&q=&f=false
UGH!
Find it by searching for Abstract homotopy and simple homotopy theory
-
- CommentRowNumber81.
- CommentAuthorHarry Gindi
- CommentTimeApr 1st 2010
Oh, sure! I knew about the google books version. I wonder if there is any way to get the publisher to sell an electronic version of it (or if you and Kamps could do it).
-
- CommentRowNumber82.
- CommentAuthorTim_Porter
- CommentTimeApr 1st 2010
I do not have an electronic copy. The manuscript was produced at Hagen, not at Bangor. In any case it is an idea to check that the things you want to know and learn about are in it!!!! This is not obvious to me. Some of the things you want are there almost certainly, but there is not much about the move to higher groupoids etc. Have you glanced at the other notes that are available (S-cat notes etc.), on my personal n-lab page. Some of that material is a summary of what went into Kamps - Porter, so is a good place to look.
-
- CommentRowNumber83.
- CommentAuthoradeelkh
- CommentTimeJun 12th 2014
- (edited Jun 12th 2014)
This is embarrassing, but I must be missing something trivial. Which of the following statements is wrong?
- There are isomorphisms for .
- The isomorphisms are compatible with the associator morphisms, so that this monoidal structure is braided.
- The braiding isomorphisms satisfy , so that this monoidal structure is symmetric.
- The Day convolution takes symmetric monoidal structures to symmetric monoidal structures.
-
- CommentRowNumber84.
- CommentAuthorZhen Lin
- CommentTimeJun 12th 2014
The isomorphisms in (1) are either not natural or not order-preserving. (To get a natural bijection, swap the two halves of ; to get an order isomorphism, do nothing.)
-
- CommentRowNumber85.
- CommentAuthoradeelkh
- CommentTimeJun 12th 2014
Right, thanks!
-
- CommentRowNumber86.
- CommentAuthoradeelkh
- CommentTimeJun 13th 2014
I find this a confusing point, so I added a small warning about it to the relevant pages (simplex category, ordinal sum, join of simplicial sets) in case other beginners might feel the same.
-
- CommentRowNumber87.
- CommentAuthorHurkyl
- CommentTimeAug 30th 2020
-
- CommentRowNumber88.
- CommentAuthorGuest
- CommentTimeMar 20th 2021
Reading the article, I think I found a typo in Section 4. Examples — Simplicial n-sphere: for the definition of S⁰, it should be ∂Δ[1] rather than ∂Δ[0], should’nt it be ?
Sorry for my english (I’m french),
adufour. -
- CommentRowNumber89.
- CommentAuthorDmitri Pavlov
- CommentTimeMar 20th 2021
1 to 89 of 89