nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorSridharRamesh
- CommentTimeFeb 23rd 2010
- (edited Feb 23rd 2010)
I've created a new article entitled algebra for a C-C bimodule, a straightforward concept encapsulating both algebras and coalgebras for endofunctors, as well as further generalities besides. There's surely a better name than using "C-C bimodule" (replacing it with "endoprofunctor", perhaps? Although I actually find that less preferable...), for someone to propose or let me know already exists, as the case may be.
(I've also made some small edits to the articles on algebras and coalgebras for endofunctors; in particular, the former had forgotten to define the morphisms of such algebras)
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeFeb 23rd 2010
There's surely a better name than using "C-C bimodule" (replacing it with "endoprofunctor", perhaps?
Yes, I like algebra for an endo-profunctor as that tells me much more about what the definition is like. I went ahead and made that a redirect. I leave it to you whether to change the entry title or not.
I also linked to the entry from natural numbers object.
-
- CommentRowNumber3.
- CommentAuthorMike Shulman
- CommentTimeFeb 23rd 2010
I agree, "algebra for an endo-profunctor" is a better title. I also found the use of "=" as a cipher confusing, so I changed it to "?".
I also forgot why bimodule and profunctor are separate pages; is there a good reason? I would suggest the material at bimodule should be moved to profunctor and the former made more of a disambiguation page, since outside of Australian category theory "bimodule" usually refers to rings.
-
- CommentRowNumber4.
- CommentAuthorSridharRamesh
- CommentTimeFeb 23rd 2010
- (edited Feb 23rd 2010)
Thanks for changing the (incorrect) statement that the forgetful functor "creates isomorphisms" into the (correct) statement that it merely reflects them; I clearly wasn't thinking properly when I wrote that.
As for the use of "=" as a cipher in describing a bifunctor, I can't remember where I picked it up, although the idea was, of course, the general idea of two horizontal lines on top of each other to represent a second argument to a bifunctor just as one horizontal line represents the first argument, the similarity to an equals sign being a mere visual coincidence. For some reason I thought that was standard notation, although I agree it's potentially confusing. (I've never even really liked even the standard instances of this kind of notation using "-" with implicit scope, preferring lambda calculus-style notation which makes the binding of variables explicit and thus clearer in nested or parallel instances.)
-
- CommentRowNumber5.
- CommentAuthorSridharRamesh
- CommentTimeFeb 23rd 2010
- (edited Feb 24th 2010)
I guess the name using "endoprofunctors" is fine. My qualm was that I felt this imputed slightly different connotations than "bimodule" did, the latter better reflecting the symmetry of the situation. But this may not have any substance outside my own head; at any rate, it is a rather minor irk, and certainly the name using "endoprofunctors" is appropriate and clear.
One observation: under the convention that a profunctor
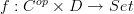 is to be thought of as going from
is to be thought of as going from  to
to  (i.e., essentially viewed as its currying
(i.e., essentially viewed as its currying 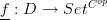 ), then what's described in the article is perhaps better called coalgebras for the profunctor (structure on carrier
), then what's described in the article is perhaps better called coalgebras for the profunctor (structure on carrier  is naturally thought of as a morphism from
is naturally thought of as a morphism from  to
to 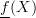 , and so on). Of course, under the opposite convention for profunctors, we get the opposite result and see it is an algebra for the dual kind of generalized functor; the concept itself is symmetric.
, and so on). Of course, under the opposite convention for profunctors, we get the opposite result and see it is an algebra for the dual kind of generalized functor; the concept itself is symmetric. -
- CommentRowNumber6.
- CommentAuthorMike Shulman
- CommentTimeFeb 24th 2010
I generally prefer not to use more than one cipher, rather than - and ? I'll generally introduce variables and maybe use a \mapsto symbol. Lambda notation is okay too, but I find it a little cluttered.
I think it's fine to call these "algebras" for an endo-profunctor whichever convention one uses, although possibly something like "dialgebra" would be even less ambiguous. I do think there are good reasons for the convention that the target of a profunctor is the contravariant variable.
-
- CommentRowNumber7.
- CommentAuthorSridharRamesh
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
Yes, left to my own devices, I often use \mapsto notation as well; that's basically lambda calculus notation, as far as I'm concerned, just with the minor variation of \mapsto on the right of the variable being bound instead of \lambda on the left of it.
I do quite like your proposal of the name "dialgebras".
-
- CommentRowNumber8.
- CommentAuthorMike Shulman
- CommentTimeFeb 24th 2010
Oh, and I'm not entirely sure what "creates isomorphisms" even means -- does it mean the functor is pseudomonic?
-
- CommentRowNumber9.
- CommentAuthorSridharRamesh
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
Well, part of the problem is that when I wrote it, I wasn't really thinking enough about what it should mean. What I had in mind was something like that F creates isomorphisms if every isomorphism with domain F(X) is of the form F(m) for some isomorphism m with domain X, with some kinds of "uniquely"s thrown somewhere [this being evil to the extent that F(cod(m)) is to be equal to the codomain of the original isomorphism, and possibly via the "uniquely"s as well].
But, upon seeing it edited away, and realizing the evilness in my original inchoate thoughts, I came to think, for a faithful functor, "creates isomorphisms", to be a non-trivial non-evil property, probably would most naturally mean "is pseudomonic", which, of course, doesn't generally hold of the relevant forgetful functor.
Oh well. Not that it matters anymore.
-
- CommentRowNumber10.
- CommentAuthorSridharRamesh
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
"I do think there are good reasons for the convention that the target of a profunctor is the contravariant variable."
It's not an issue I've thought very much about, or have strong emotions regarding, but I've asked a question about what these are on the page on profunctors (mainly, if there are further reasons beyond a preference for the covariant Yoneda embedding into contravariant functors over the contravariant Yoneda embedding into covariant functors).
(Also, I'm afraid I don't know how to code the quoting of a post on this board) -
- CommentRowNumber11.
- CommentAuthorDavidRoberts
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
If you do a greater than symbol
>
at the beginning of a paragraph in markdown mode then you get the pretty blue box -
- CommentRowNumber12.
- CommentAuthorSridharRamesh
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
Ah, thanks.
-
- CommentRowNumber13.
- CommentAuthorMike Shulman
- CommentTimeFeb 24th 2010
I added a universal characterization of these algebras involving extranatural transformations, which I think is an additional argument in favor of "dialgebras" (since extranatural transformations are a special case of dinatural ones, and "extra-algebra" is too cumbersome (-: ).
-
- CommentRowNumber14.
- CommentAuthorFinnLawler
- CommentTimeSep 17th 2010
I was going to absorb algebra for a profunctor (and algebra for an endofunctor) into a new page called algebra for an endomorphism, but I noticed something wasn’t quite right. Sridhar wrote:
what’s described in the article is perhaps better called coalgebras for the profunctor
The things described here really are coalgebras in Prof, under the bijections
In the case of a functor , a ’dialgebra’ in this sense for , hence an algebra for , is the same as an algebra (in Prof) for .
I’m reluctant to go ahead with any edits, because I don’t know (a) whether this concept has appeared in the literature, (b) how important it is or (c) what anyone else thinks is the naturally prior concept. Thoughts?
-
- CommentRowNumber15.
- CommentAuthorMike Shulman
- CommentTimeSep 17th 2010
What was your definition of “algebra for an endomorphism” going to be?
-
- CommentRowNumber16.
- CommentAuthorFinnLawler
- CommentTimeSep 17th 2010
Just the underlying data for an algebra over a monad – given in a bicategory, an algebra would be a 1-cell together with a 2-cell .
-
- CommentRowNumber17.
- CommentAuthorMike Shulman
- CommentTimeSep 18th 2010
But an algebra for an endo-profunctor isn’t of that form. Oh, that was why you came here to comment in the first place.
Actually, I would be against subsuming algebra for an endofunctor into algebra for an endomorphism – having the latter too would be fine, but there’s so much to say about algebras for endofunctors, and being the most important example of algebras for endomorphisms, that I think they should be on their own page.
-
- CommentRowNumber18.
- CommentAuthorFinnLawler
- CommentTimeSep 23rd 2010
I’ve now created algebra for an endomorphism, left algebra for an endofunctor alone, and made some edits to algebra for a profunctor.
-
- CommentRowNumber19.
- CommentAuthorFinnLawler
- CommentTimeSep 23rd 2010
By the way, is there a way to get horizontal lines/rules in
\arrays? I want to use inference-rule syntax for the bijections at algebra for a profunctor. -
- CommentRowNumber20.
- CommentAuthorMike Shulman
- CommentTimeMar 17th 2017
There’s a reference request for this page at http://mathoverflow.net/questions/264793/algebras-over-endo-profunctors
-
- CommentRowNumber21.
- CommentAuthorMike Shulman
- CommentTimeJul 4th 2021
It would be useful to rename this discussion so that it gets picked up by the “Discuss this page” link at algebra for a profunctor.
(Prompted by another reference request on Zulip.)
1 to 21 of 21