nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Discussion Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
- (edited Jan 23rd 2013)
added to Set the statement that
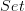 is the terminal topos.
is the terminal topos. -
- CommentRowNumber2.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 24th 2010
I added the modifier 'Grothendieck' to topos, since for example there is no geometric morphism
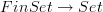 .
. -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
Ah, right. Thanks.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
hm, but then I have a mistake in the section global section functor on a general topos...
-
- CommentRowNumber5.
- CommentAuthorMike Shulman
- CommentTimeFeb 24th 2010
Why is the left adjoint in that section called "LConst" rather than "Const"?
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
Why is the left adjoint in that section called "LConst" rather than "Const"?
For two reasons:
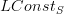 is the constant sheaf of locally constant functions! The sheaf is named after what it is "a sheaf of".
is the constant sheaf of locally constant functions! The sheaf is named after what it is "a sheaf of".for
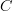 a site, the functor
a site, the functor 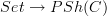 should be called
should be called 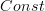 . Then with
. Then with 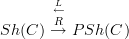 the geometric embedding, we have the pleasant
the geometric embedding, we have the pleasant 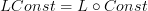
-
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeFeb 24th 2010
Hmm, I guess I see that, but my intuition is that Const(X) should be the constant sheaf on X.
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
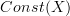 should be the constant sheaf on
should be the constant sheaf on  .
.Well, it's called the "constant sheaf" of course. I still found it a great idea to write
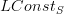 for the constant sheaf on
for the constant sheaf on 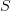 . Originally I kept writing
. Originally I kept writing 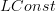 with a little space to amplify that it is the sheafification of the constant presheaf. Then it seemed like a neat idea to just discard the space.
with a little space to amplify that it is the sheafification of the constant presheaf. Then it seemed like a neat idea to just discard the space.I think it fits nicely into the pattern. This way for instance we have precisely that
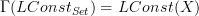 is the set of locally constant functions.
is the set of locally constant functions.More generally, for
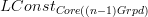 the constant
the constant  -stack on the n-groupoid of (n-1)-groupoids, we have
-stack on the n-groupoid of (n-1)-groupoids, we have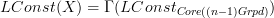
is precisely the n-groupoid of locally constant (n-1)-stacks. So that works very nicely. If I write
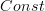 instead of
instead of 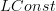 here a very nice abstract pattern is severely broken by the notation.
here a very nice abstract pattern is severely broken by the notation.Or so I think.
-
- CommentRowNumber9.
- CommentAuthorMike Shulman
- CommentTimeFeb 25th 2010
I just find it confusing to write "LConst" for the functor which constructs constant sheaves -- my mind keeps trying to read it as a functor which constructs locally constant sheaves. In general I think it's more common to name functors after what they do to objects, not to the elements of those objects. For instance, we say "the free monoid functor" not "the words functor," and "the free strict oo-category functor" not "the pasting diagrams functor." Probably you agree that the functor is "the constant sheaf functor," but then I think the notation of the functor should reflect the name of the functor.
-
- CommentRowNumber10.
- CommentAuthorDavidRoberts
- CommentTimeFeb 25th 2010
I think there are some level-type conflations here. The constant stack with fibre the groupoid Set is the stack of locally constant sheaves. The constant sheaf with fibre F is the sheaf of locally constant functions with values in F.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeFeb 25th 2010
In general I think it's more common to name functors after what they do to objects, not to the elements of those objects
Here is an idea: would it help if I write
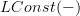 systematically?
systematically? -
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeJan 23rd 2013
added to Set a brief paragraph Set -- Properties -- Opposite category and Boolean algebras
-
- CommentRowNumber13.
- CommentAuthorTodd_Trimble
- CommentTimeJan 23rd 2013
I sharpened Urs’s paragraph. Incidentally, I didn’t understand why this was cast in a definition environment (definition 1).
-
- CommentRowNumber14.
- CommentAuthorUrs
- CommentTimeJan 23rd 2013
Thanks!
The Definition-environment was supposed to be a Proposition-environment. I have changed it now. (This happens because I grab the code for these environments from the Instiki-Theorems page where it is the Definition-environment that is written out. Here I forgot to edit it after copy-and-pasting.)
-
- CommentRowNumber15.
- CommentAuthorIngoBlechschmidt
- CommentTimeApr 11th 2014
Added to Set the following remark:
“In constructive mathematics, defines an equivalence of with the opposite category of that of complete atomic Heyting algebras. In fact, for any elementary topos , the power object functor defines an equivalence of with the opposite category of that of internal complete atomic Heyting algebras. (This phrase can be interpreted using the internal language of .)”
Note that at complete atomic Boolean algebra, there is the following very interesting statement:
“This property of CABAs is not applicable in constructive mathematics, where power sets are rarely boolean algebras. However, we can use discrete locales instead (or rather, their corresponding frames). That is, define a CABA to be (not a complete atomic boolean algebra but) a frame such that the locale maps and (which in the category of frames are maps and ) are open (as locale maps). Then it should be (I will check) a classical theorem that CABAs and complete atomic boolean algebras are the same, and a constructive theorem that CABAs and power sets are the same (in the same functorial manner as above).”
This is should really be checked someday. I will do it, but not now.
-
- CommentRowNumber16.
- CommentAuthorUrs
- CommentTimeMay 20th 2023
added pointer to:
- Saunders MacLane, §IV.10 of: Categories for the Working Mathematician, Graduate Texts in Mathematics 5 Springer (1971, second ed. 1997) [doi:10.1007/978-1-4757-4721-8]
-
- CommentRowNumber17.
- CommentAuthorvarkor
- CommentTimeJan 3rd 2024
What does the phrasing:
As a groupoid, is […]
mean on this page? Is it referring to the groupoid of sets and bijections?
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeJan 3rd 2024
This paragraph seems to originate in revision 32 signed by “Anonymous” in Feb 2021.
But yes, it must be referring to the core groupoid. I have made a little edit to clarify.
1 to 18 of 18