nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
started category fibered in groupoids as I think this deserves a page of its own separated from Grothendieck fibration
I understand that there was some terminological opposition voiced at Grothendieck fibration concerning the term "category cofibered in groupoids", but am I right that this does not imply opposition against "category fibered in groupoids", only that the right term for the arrow-reversed situation should be "opfibration in groupoids"?
-
- CommentRowNumber2.
- CommentAuthorzskoda
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
Lurie uses "category cofibered in groupoids" in HTT. This is a traditional term and I vote for it.
The opposition follows Gray's argument about incompatibility with the property of cofibration in homotopy theory, while the position takes the cocartesian arrow to define cofibered and cartesian arrows to define fibered. They define the usual cartesian and cocartesian arrows in the special cases of codomain fibration and domain cofibration respectively.
-
- CommentRowNumber3.
- CommentAuthorTim_Porter
- CommentTimeFeb 24th 2010
I find Lurie's use very confusing. I know that Grothendieck introduced 'cofibred' categories, but he did not have the term cofibration in a key meaning in other parts of the discussion. Semantically a fibred category does reflect the image of fibres as in a fibre bundle. The way the change of object determine the lift is not completely dual so there is no necessity to use a 'co'. The solution put by the categorical school of using op does work, but is ugly. I personally came to fibred categories from a more homotopy theoretic POV and so find even the use of `cartesian' slightly odd. The terminology is really a mess and is very non-intuitively based. A category (co)fibred in groupoids is not a category, it is a functor, in fact it IS a fibration with fibres that are groupoids. I found this all confusing when I first met it and could not see why such a daft terminology was used. I still find it daft. If I was to vote between fibred and cofibred, I would say do not use either since the terminology is stupidly bad, and 'fibration fibred in groupoids' is unambiguous, provided one also has op-fibration defined.
I am afraid I do not think that tradition counts much in this as there are two traditions one in alg. geom and probably non-abel. cohomology , the other the large body of category theory. (By the way what does Benabou use in his work on 'fibred categories'. I have not got a copy here with me.) The older tradition is Grothendieck's but that is not a deciding factor. In any case we need a section which points out the different uses and explains some of the points of the argument for any against, but in fairly clear way!
-
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
A category (co)fibred in groupoids is not a category, it is a functor
I disagree with this. Grothendieck emphasised relative point of view. Thus S-schemes and categories over categories or categories in comma category. It is very suggestive for functor point of view of geometry. It has a suggestive intutive meaning enhancing mere "functor" to which you would like to degrade it and allows terminology like Cartesian functor for specific morphisms between categories over categories preserving cartesian arrows.
For Benabou's point of view you can look in online notes of Streicher which are excellent: http://www.mathematik.tu-darmstadt.de/~streicher/FIBR/FibLec.pdf.gz
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
er, I am confused. What's your opinion on my choices in the entry, now? I say "category fibered in groupoids" for the things
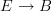 that are classified by functors
that are classified by functors 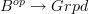 .
.Agreed, or not?
-
- CommentRowNumber6.
- CommentAuthorHarry Gindi
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
(Weak) presheaf of groupoids is really the correct notion, but this requires a preferred choice of cleavage. I like the fibered category notion somewhat better because it takes all of these weak presheaves and shows that they're equivalent. I agree, this puts us in a tight spot. The problem is that it's an abstraction of the notion of a "discrete fibration" rather than a topological fibration.
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
- (edited Feb 24th 2010)
(Weak) presheaf of groupoids is really the correct notion,
I don't see why this is "more correct" than the dual notion. The point is that given any pseudofunctor
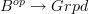 we may pull back the functor
we may pull back the functor 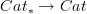 and obtain a functor
and obtain a functor 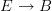 . We ask which functors with codomain
. We ask which functors with codomain 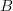 arise this way.
arise this way. -
- CommentRowNumber8.
- CommentAuthorMike Shulman
- CommentTimeFeb 24th 2010
I tend to say "fibration" myself but I do think of them as "relative categories over a base" -- the term "indexed categories" is also common for the same reason, but I think "fibered category" is fine once you get used to it. In topology people also talk about a "ex-space parametrized over B" to mean a "relative" fibration-like notion (although confusingly, they tend to use the word "relative" to mean something under a space). My main objection is to the use of "cofibered" because it comes along with "cofibration" which is, I think, very misleading. We have a perfectly good unambiguous prefix "op-" that also conveys the meaning of a dualization.
@Harry: I think categorical fibrations are a common generalization of topological fibrations and of discrete categorical fibrations. At least, fibrations between 1-types are the same as categorical fibrations between groupoids, and when you generalize to (oo,1)-categorical fibrations then you include all ordinary fibrations between oo-groupoids = homotopy types.
-
- CommentRowNumber9.
- CommentAuthorTim_Porter
- CommentTimeFeb 24th 2010
@ Zoran S-schemes are not straightforward schemes. They are schemes over ... , but the shorthand terminology is useful. Comma categories are categories. Categories over another a category ... that is fine. Category (co)fibred in groupoids is ambiguous to me. Take two groupoid G and H and form G\times H. That is a category (co)fibred in groupoids !!! but in two distinct ways, so the terminology is vague. It is usual, but so is the terminology 'let f(x) be a function defined on some (specified) subset of the reals'. You can say little precise about f in terms of its properties as a function unless you specify what its codomain is. That phrase is traditional 'analysis speak', but it is bad terminology. It is easy and was done in good texts, to make the point clear at the start near the definitions, even if sometimes later on one allows some slackening of the precision.
In any case I insist that a category (co)fibred in groupoids is not a category E, it is a functor $E\to B$, with a lot of important extra properties, because if I say a group is a set, that is true even if it is silly to leave it there. I do not 'like to degrade it' to functor. It is a functor. It is not just a functor, of course. Grothendieck made some excellent choices of terminology and some less good ones. This, in my opinion, is one of the latter.
The other terminology you mention such as Cartesian functor seem fine by me. A Cartesian functor is a functor satisfying some properties. Fine. (I do not think that 'Cartesian' is a particularly apt term for it, as it seems to have little to do with Descartes! but that is another issue. I do not happen to like Cartesian product as a term. I do not have something against Descartes, iI do not see why product would not suffice.)
A fibration is part of a categorification process, going from a simple category and functors situation towards 2-categories etc. I think that aspect is disserved by strict adherence to either of the traditional terms.
@ Urs. My proposal would be to define fibration and op-fibration (as they probably have been), then in a new entry called possibly 'fibration fibred in groupoids' have (i) a list of properties and the classification (and I think that is what I would call a fibration, but I may be wrong on that) (ii) have a section 'terminological differences and synonyms' or something like that, in which some of the history is put down, and some of the arguements that Zoran puts forward are put as well as the categorical one, and then to say that because of the possibility of confusion we adopt a neutral term that emphasises that it is a fibration with additional properties. then there would be links etc to the terminology
The term 'fibration fibred in groupoids' does pick up the relative nature of the object, but in a relative situation there has to be information about relative to what and what is the relationship involved. A vector bundle is a 'fibre bundle fibred in vector spaces'.
-
- CommentRowNumber10.
- CommentAuthorHarry Gindi
- CommentTimeFeb 24th 2010
@Mike: Op is really a terrible prefix. It ends in a voiceless bilabial plosive, which makes the word sound disjointed.
-
- CommentRowNumber11.
- CommentAuthorDavidRoberts
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
Tim wrote:
it is a functor
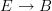
I agree. When I read your first declamation that it was a functor, I thought (and possibly so did others, based on their comments) you meant a functor
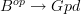 , which I do not like to call a fibred category. It's a bit like calling a map
, which I do not like to call a fibred category. It's a bit like calling a map 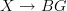 a principal
a principal 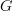 -bundle to my mind.
-bundle to my mind. -
- CommentRowNumber12.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 25th 2010
Harry, "op-fibration" is standard established terminology.
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
okay, following Tim's suggestion I renamed the entry into fibration fibered in groupoids, made about 50 variants of this redirects and added a brief remark on old terminology.
Please, you all, feel encouraged to edit the entry if you have further ideas how to improve it. Don't invest effort in trying to make me do it. I am busy with something else! :-)
-
- CommentRowNumber14.
- CommentAuthorHarry Gindi
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
@Todd: That I don't deny. I was merely noting that it was an unfortunate choice. However, the terminology "cofibered in groupoids" is equally well-established, if not moreso. I think it's a question of what field you're in.
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeFeb 25th 2010
Well, while "op-fibration" may sound too voiceless-bilabial-plosively to you, the problem with "cofibration"is that it badly collides with the other widely spread notion (and widely spread in the same field!).
-
- CommentRowNumber16.
- CommentAuthorHarry Gindi
- CommentTimeFeb 25th 2010
My point was to come up with something that sounds better than opfibration.
-
- CommentRowNumber17.
- CommentAuthorDavidRoberts
- CommentTimeFeb 25th 2010
If we are looking at renaming things (which may not be the case), I like the idea of calling a fibration in this setting a Grothendieck fibration - other fibrations have names attached to them (Serre, Hurewicz etc). Then an opfibration can be a co-Grothendieck fibration. This is assuming that Grothendieck came up the idea, and I vaguely recall Gabriel did some work on them. Gabriel-Grothendieck fibration then?
-
- CommentRowNumber18.
- CommentAuthorHarry Gindi
- CommentTimeFeb 25th 2010
I agree with the above sentiment.
-
- CommentRowNumber19.
- CommentAuthorSridharRamesh
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
other fibrations have names attached to them (Serre, Hurewicz etc.)
And let's not forget the Hopf fibration... Say, I like the sound of that. :)
Speaking of which, what's so bad about voiceless bilabial plosives (aka, the phoneme /p/)?
-
- CommentRowNumber20.
- CommentAuthorMike Shulman
- CommentTimeFeb 25th 2010
@Harry, you just haven't said "opfibration" enough. (-: It becomes quite easy with a little bit of practice.
I think it was well said that the only thing worse than bad terminology is continually changing terminology. Established terminology has to be quite bad for it to be worth changing. I think "cofibration" is in that category (collision with another well-established and completely different term) but "opfibration" is definitely not (only being, maybe, slightly difficult to say).
I find it tiresome to always add "Grothendieck" in front of "fibration," but when disambiguation is necessary it's a good idea. I like "Grothendieck opfibration" better than "co-Grothendieck fibration," but I would certainly know what was meant by the latter. Dualizing people's names sounds a little odd. But "Grothendieck fibration" is certainly better than "Cartesian fibration," which adds yet another meaning to the way-overworked word "cartesian."
-
- CommentRowNumber21.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 25th 2010
I'll add that if you're upset with opfibration, you probably need to relax with a nice warm bath. With Epsom salts. ;-)
-
- CommentRowNumber22.
- CommentAuthorHarry Gindi
- CommentTimeFeb 25th 2010
I'm just saying that people who I've said the word opfibration in front of have grimaced at the sound of the word. I'm not against it for any reason other than this.
-
- CommentRowNumber23.
- CommentAuthorDavidRoberts
- CommentTimeFeb 25th 2010
nice voiceless bilabial plosive there Todd
-
- CommentRowNumber24.
- CommentAuthorHarry Gindi
- CommentTimeFeb 25th 2010
=( It's aspirated before fricatives like s and f.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeFeb 25th 2010
But "Grothendieck fibration" is certainly better than "Cartesian fibration," which adds yet another meaning to the way-overworked word "cartesian."
True. On the other hand at Grothendieck construction there is a complaint that "Grothendieck" is a way-overworked word, too! :-) Given the other meanings of "cartesian", at least "Cartesian fibration" tries to be descriptive. So for the higher categorical versions I tend to prefer it over "n-Grothendieck fibration" or the like. But I see that this means treating Descartes differently from Grothendieck...
-
- CommentRowNumber26.
- CommentAuthorHarry Gindi
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
I think that an answer here is not to call it a fibration at all. Vistoli has a little remark in his notes, where he says that morally, a fibered category should be called a prestack of categories, a category fibered in groupoids should be called a prestack of groupoids, a prestack should be called a separated prestack, and a stack should be called a stack. I like the term stack rather than sheaf in this instance because it emphasizes the fact that we haven't at any point chosen a cleavage. If I were teaching a course, I would actually go along with this terminology.
-
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeFeb 25th 2010
Right, but as was said above: "stack" etc is really a word for functors
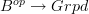 , not for the functors
, not for the functors 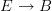 that these classify under the Grothendieck constrution.
that these classify under the Grothendieck constrution.So calling a fibration a (pre)stack is fine once the Grothendieck construction and the equivalence that it indues is understood. But it is confusing in a discussion that wants to establish the Grothendieck construction equivalence. How do you prove an equivalence, if your terminology does not allow you to distinguish between the two things you want to prove are equivalent?!
-
- CommentRowNumber28.
- CommentAuthorHarry Gindi
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
In Grothendieck's original formalism, a stack is precisely the functor
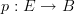 . You can see this in Vistoli's notes, which are based on EGA and SGA. I could find the original references for you.
. You can see this in Vistoli's notes, which are based on EGA and SGA. I could find the original references for you.The equivalence of these notions that you mention is so ingrained in our conciousnesses that we've identified the notion of a "stack" and a "sheaf".
The imagery is fairly clear if you think about it for a moment. We've got a category sitting on top of another category with a "surjective functor" that "compresses the stack". At least that's how I look at it.
-
- CommentRowNumber29.
- CommentAuthorzskoda
- CommentTimeFeb 25th 2010
Tim said:
S-schemes are not straightforward schemes. They are schemes over ...
The GENERAL notion of a scheme in terms of categories of qcoh sheaves is necessarily relative as exaplained convincingly in Rosenberg's paper Noncommutative scheme. What Grothendieck called a scheme is scheme above Spec Z or categorically over the category of abelian groups. In noncommutative and many other cases we do not have that luxury.
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeFeb 25th 2010
In Grothendieck's original formalism, a stack is precisely the functor
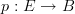
Is that so? Hm, then we are al suffering from repeated bad change of terminology. Because nowadays "stack" is predominantly used for the thing
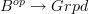
-
- CommentRowNumber31.
- CommentAuthorTim_Porter
- CommentTimeFeb 25th 2010
@ Zoran: I agree with you completely on that, but too rigorous application of that leads to a bit of a problem. Any object in any category which has a terminal object can also be thought of as being the unique map to that terminal object. This gets something like an infinite regress!
No one would do that I hope, and, I agree, for the extensions to more complex situations that first step in an important one to take. In the n-cat community one can also make an analogy with 2-spaces where the relative case is again useful. Space over B is an essential concept, of course. My argument is that once a definition and intendant intuition is got across then one can start being a bit lax with the terminology so Scheme over Spec(S) can be introduced and then one say something like 'It is usual to use the shorter term 'S-scheme' to refer to a scheme over Spec(S)' and so on. It is probably not so good to use that lax language too much before the intuition has had a chance to grew a few roots and even then from time to time a little reminder of the original version may be a good thing.
-
- CommentRowNumber32.
- CommentAuthorzskoda
- CommentTimeFeb 25th 2010
Any object in any category which has a terminal object can also be thought of as being the unique map to that terminal object.
Maybe I was not clear: choosing the base scheme makes sense of local affiness: the elements of the affine cover correspond to the categories of qcoh sheaves which are monadic over the base scheme (and a bit more than that, not to be technical here). For some other kinds of spaces, this is not important, but it is essnetial for the notion of a scheme.
-
- CommentRowNumber33.
- CommentAuthorTim_Porter
- CommentTimeFeb 25th 2010
@ Zoran I see what you are meaning now. It is a long time since I read substantial parts of Alg Geom and although the terminology and viewpoint has shifted slightly I recall understanding the point you are making.
Perhaps that point of view leads to a different terminology that is something as follows: E\to B is a B-category fibred in groupoids if.... . That gets around my objection to some extent as a B-category is a category plus something.
On that line of thought I wonder if anyone here has thought of the X-manifolds that Turaev uses in his HQFT papers from this point of view. These are manifolds over a space X which is thought of as a classifying space of some group or more generally. I plan to discuss this in some Lab entries once I have thought out my version of his stuff for some notes corresponding to my two Almeria workshop lectures.
-
- CommentRowNumber34.
- CommentAuthorzskoda
- CommentTimeFeb 25th 2010
Right, B-category fibred in groupoids is more precise.
-
- CommentRowNumber35.
- CommentAuthorTim_Porter
- CommentTimeFeb 25th 2010
That still would not resolve the cofibred against fibred clash of cultures!
Although it is very useful 'co-' can be awkward!
-
- CommentRowNumber36.
- CommentAuthorSridharRamesh
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
=( It's aspirated before fricatives like s and f.
I guess I don't see the relevance of this. Sure, English phonology has /p/ aspirated in many contexts, and unaspirated in some other contexts. But so what? I still don't understand what's so bad about /p/, aspirated or not.
The people who grimace at the sound of "opfibration", do they also grimace at "stepfather" and "campfire" and "top five"? Anyone who can handle "top five" should be able to handle "opfibration"...
-
- CommentRowNumber37.
- CommentAuthorHarry Gindi
- CommentTimeFeb 25th 2010
Op is not a word by itself. Having an aspirated p right after a prefix sounds really bad.
-
- CommentRowNumber38.
- CommentAuthorSridharRamesh
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
It does? I haven't noticed myself or others to be afflicted by any such particular aversion. If "stepfather" and "campfire" don't count because they can be thought of as two words each (like "top five"), then what about "capsule" or "hipster" or "tipsy" or myriad other such words? (Alright, yeah, "cap", "hip", and "tip" are also words in themselves, but that hardly matters to the way these sound... If you like, the easiest solution would just be to consider "op" a word, then. We can speak of the "op" of a category and so forth. Think of "opfibration" as "op fibration", if it helps. Not that I still see why this would be necessary.)
-
- CommentRowNumber39.
- CommentAuthorHarry Gindi
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
When I say it aloud, I prefer to say "oppositely fibered in groupoids" rather than the odious "opfibered in groupoids". I'd be happy to call it "antifibered in groupoids" and an "antifibration".
-
- CommentRowNumber40.
- CommentAuthorTodd_Trimble
- CommentTimeFeb 25th 2010
<div> <blockquote> Having an aspirated p right after a prefix sounds really bad. </blockquote> <p>I disagree, but let's please terminate this discussion. It's leading us nowhere and getting ridiculous.</p> </div> -
- CommentRowNumber41.
- CommentAuthorHarry Gindi
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
Since this is on the internet, I know some of you might be unable to judge my tone. This is at the level of seriousness of polite banter. =).
Let's just say that in my perfect world, I wouldn't call it an opfibration, but I'm well aware that my opinion doesn't (and shouldn't!) count as much as yours, simply by seniority and the fact that you've all done significant work. I am willing to defer to your expertise and judgement (collectively).
-
- CommentRowNumber42.
- CommentAuthorSridharRamesh
- CommentTimeFeb 25th 2010
let's please terminate this discussion. It's leading us nowhere and getting ridiculous.
Fair enough. (And, Harry, take as comfort that my opinion also doesn't count for much, for the same reasons. :))
1 to 42 of 42