nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeFeb 24th 2010
started a stubby nPOV-description at the beginning of BV-BRST formalism
somebody please stop me, though, because I urgently need to be doing something else... :-)
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeFeb 25th 2010
briefly mentioned this in a section nPOV -- In Physics at nPOV.
I think we can eventually go further here. The Ben-Zvi/Nadler article that is cited in the above entry makes crystal clear how the applications of supergeometry and NQ-supermanifolds in this business are really secretly a hack for genuine derived geometry, i.e.
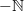 -graded supergeometry.
-graded supergeometry.But I have to run now
-
- CommentRowNumber3.
- CommentAuthorzskoda
- CommentTimeFeb 25th 2010
There is also an entry BV theory. On my own pages I started eventually related entry Kozsul complex (zoranskoda).
From the point of view of physics geometric supersymmetry is much less important than the proposal for "space time supersymmetry".
-
- CommentRowNumber4.
- CommentAuthorzskoda
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
Hey, there is no entry! where did I loose it ??
Oh, it is not in my personal lab it is in nlab Koszul complex. I am having a multiple personality problem :)
P.S. I do not like the title "BV theory" at all. It is not a theory in the sense of physics.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeFeb 25th 2010
- (edited Feb 25th 2010)
I do not like the title "BV theory" at all.
Right, me neither. I have renamed that entry therefore, you have to look at BV-BRST formalism. It is only the Cache bug that is responsible for the fact that the old page on "BV-theory" still displays at all.
-
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeFeb 26th 2010
- (edited Feb 26th 2010)
concerning the statement from the article that is now cited at BV-BRST complex:
on page 23, beginning of section 32 it says that
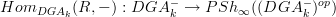 is a stack on
is a stack on 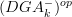 "since it distributes over limits in
"since it distributes over limits in 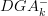 ".
".I must be missing something obvious: how does that make it a stack? It need not preserve the limits that exist in the site^op, but those that the topology forces to become limits...
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeFeb 26th 2010
- (edited Feb 26th 2010)
I see now a proof page 43 on in Toen's Champs affine
Toen also has the more categorical statement here in that he talks about simplicial objects in dgAlg^op.
I think this is really important, because it seems to me that what is really going on here is that for suitable oo-sites the claim is that we have an oo-adjunction
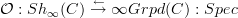
where
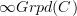 means the oo-category of groupoid objects in C.
means the oo-category of groupoid objects in C.Then the statement for dg-algebras folllows, I think, with
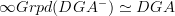 , using oo-Dold-Kan followed by the total complex construction. If you see what I mean.
, using oo-Dold-Kan followed by the total complex construction. If you see what I mean. -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeFeb 28th 2010
- (edited Feb 28th 2010)
the adjunction
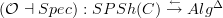 that Toen discusses around p. 43 is precisely the adjunction that I discuss on my page Chevalley-Eilenberg algebra on my personal web, only that I look at oo-stacks over smooth algebas^op where he looks at plain algebras^op.
that Toen discusses around p. 43 is precisely the adjunction that I discuss on my page Chevalley-Eilenberg algebra on my personal web, only that I look at oo-stacks over smooth algebas^op where he looks at plain algebras^op.His
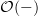 is my
is my 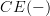 .
.It seems that one consequence of this which Toen and later Ben-Zvi/Nadler emphasize and which I didn't fully appreciate is that we want to be serious with composing this with the Quillen equivalence between
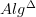 and commutative dg-algebras. This gives a nice nPOV description of rational homotopy theory and Sullivan models:
and commutative dg-algebras. This gives a nice nPOV description of rational homotopy theory and Sullivan models:let
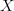 be a topological space, regarded as an oo-groupoid. Then applying
be a topological space, regarded as an oo-groupoid. Then applying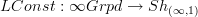
regards it it as an oo-stack (the constant oo-stack of locally constant oo-stacks with values in X :-)
Then applying
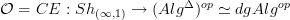
computes a dg-algebra of this, by assigning to each k-cell an algebra quasi-isomorphic to the ground field, such as an algebra of differential forms on the k-simplex. So that (when cofibrantly replaced) yields the Sullivan model for X !
Then applying
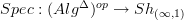
regards this algebraic model as an oo-stack again. To see what this oo-stack is like, we can forget all its extra structure and just remember the unstructured oo-groupoid it represents by applying the global sections functor
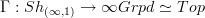
Toen's theorem 2.5.1 shows that this is a space weakly rationally eqjuivalent to X .
In fact, if you look at what is happening here, these last two steps give Sullivan's prescription for the constructon of a topological space from a dg-algebra.
-
- CommentRowNumber9.
- CommentAuthorzskoda
- CommentTimeJul 21st 2010
I added the link to a neat MO answer into BV/BRST formalism and merged last two sections.
-
- CommentRowNumber10.
- CommentAuthorEric
- CommentTimeJul 21st 2010
I added a redirect so that your link will work :)
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeJul 21st 2010
by the way, Eric, in that MO reply you see the limit being mentioned that I told you about in the thread about limits:
it says there that the algebra of functions on the constraint surface is modeled (naively) as
But that’s a coequalizer in algebras
(The notation being somewhat abusive).
Dually that’s a limit. The BV-part of BV-BRST is a “resolution” of this limit, namely it realizes it as a homotopy limit.
-
- CommentRowNumber12.
- CommentAuthorEric
- CommentTimeJul 21st 2010
Gulp :)
As an aside, the more I learn, the more disappointed I become. The “awe” is disappearing. Especially when it comes to physics. I don’t think anyone really understands anything better today than we did 75 years ago. I see people using a bunch of fancy tools to tackle questions whose foundations are questionable to begin with.
How do you know you are even walking in the right direction?
-
- CommentRowNumber13.
- CommentAuthorJohn Baez
- CommentTimeJul 21st 2010
- (edited Jul 21st 2010)
Eric wrote:
As an aside, the more I learn, the more disappointed I become. The “awe” is disappearing. Especially when it comes to physics.
As far as math goes, my awe level keeps going up, especially when I relax, stop trying to keep up with what other people are doing (math as a competitive business), and simply think about what whatever I like. There are really deep mysteries which we are getting closer to understanding, yet grow and expand the more we learn about them. Like the Riemann hypothesis, to take a sort of random example. At first it seems like a mildly entertaining question about whether a bunch of zeroes of some function lie on a line, with a cute application to the asymptotic density of primes. But then you see it’s related to a mysterious dynamical system, and the geometry of a mysterious space such that functions on this space are integers, and “the mysteries of the real prime”, and the equally mysterious “field with one element”, and “the search for a deeper base”… and you start to suspect that it’s not a puzzle we’ll solve by simply blundering around and working harder using known techniques, but something that could - if we let it! - force a revolution in basic concepts.
In short, math has layers of depth that one can probe only by sustained thought, which lead one to ever more staggeringly cosmic insights… and there’s no sign I see that this process is anywhere close to being done.
Which is why it’s a pity civilization may not last long enough for humankind to get to the really cool stuff.
How do you know you are even walking in the right direction?
In math, it’s surprisingly easy to tell when you’re walking in a right direction, and Urs is certainly walking in one.
When it comes to physics, there’s the element of trying to guess what Nature likes best, and that’s much more tricky - there’s an extra element of chance or luck or fate involved…
-
- CommentRowNumber14.
- CommentAuthorTodd_Trimble
- CommentTimeJul 21st 2010
The “awe” is disappearing. Especially when it comes to physics. I don’t think anyone really understands anything better today than we did 75 years ago. I see people using a bunch of fancy tools to tackle questions whose foundations are questionable to begin with.
That’s a pretty wide tar-brush there, Eric. Care to explain what you mean more specifically?
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeJul 21st 2010
- (edited Jul 21st 2010)
Concering physics (by which I take it is meant fundamental physics):
I see us entering in a valuable consolidation phase. In the 80s and 90s there was an explosion of ideas that overstretched what the community could cope with, to the extent that many now think it was all wasted.
But the opposite is true: we are seeing now these ideas finally be worked out and fixed.
Just focus on Edward Witten, arguably the epicenter of that explosion of ideas. Did you see his last article? This is somewhat remarkable: is a followup of
E. Witten, Some computations in background independent Open-String Field Theory , Phys. Rev. D47 (1993) 3405-3410.
E. Witten, Quantum background independence in String Theory
These had been visionary articles. Back then in the 90s this was taken as the way physics should be done. But of course these articles had gaps. The new one now observes that using AQFT techniques, these gaps can be filled.
I think everybody who has been following the scene in the last two decades or so will appreciate that something noteworthy is going on when finally AQFT methods are being applied to demonstrate the infinitesimal background independence of the string perturbation series.
As another example, consider the development of TCFT. That’s quite amazing. Witten has been talking about the A-model and the B-model for ages, Kontsevich has been making famous conjectures about it. Now it suddenly exists.
Witten had argued in 1992 that the string perturbation series for the A- and the B-model – i.e. the thing that computes the physics in the emergent spacetime that these models describe strings propagating in – is Chern-Simons theory. That has now suddenly become a theorem (due to Costello).
I think these developments are most remarkable. I think eventually the whole development to or so (before the effective collaps of the system) of fundamental physics will be redone now, with the appropriate tools that were missing back then.
I believe this to the extent that I am co-editing a book based on this statement: Mathematical Foundations of Quantum Field and Perturbative String Theory (schreiber)
-
- CommentRowNumber16.
- CommentAuthorEric
- CommentTimeJul 21st 2010
- (edited Jul 21st 2010)
That’s a pretty wide tar-brush there, Eric. Care to explain what you mean more specifically?
First, let me repeat I was talking about physics and not mathematics. Historically, the two have progressed hand in hand, but I do not see that happening anymore. I am hopeful that things will change, but I’m not very happy with the direction physics has gone. I think and have always thought that (higher) category theory will provide a language to “bring things back home” for physics, but I haven’t seen anything in a long time (except maybe a few glimmers with Kantization) that tells me we’re any closer.
Back when I was a physics student, I was fascinated by the Einstein-Bohr debates, but I always interpreted the outcome differently than most. I think most physicists today would argue that among the two, Bohr was “most right”. I guess I never gave up on Einstein. I still expect him to be vindicated one day. With the “triumph” of Bohr, physicists stopped asking questions. Giants like Feynman warned:
“I think it is safe to say that no one understands quantum mechanics. Do not keep saying to yourself, if you can possibly avoid it, ’ But how can it be like that?’ because you will go ’down the drain’ into a blind alley from which nobody has yet escaped. Nobody knows how it can be like that.”
Consequently, many people (sheep?) decided to stop asking those questions: “How can it be like that?”
But in my opinion, if you are not asking that question, you are not truly a physicist as Einstein probably would have defined it because that is the only question that should matter to a physicist: “How can it be like that?”
-
- CommentRowNumber17.
- CommentAuthorEric
- CommentTimeJul 21st 2010
Urs said:
Just focus on Edward Witten
It is funny you mention Witten because Witten is exactly the person that inspired me to proclaim my unhappiness in comment #12 :)
Zoran modified Edward Witten. I followed the link to his web site and had a look at the prominently linked article
The opening paragraph is pure rubbish.
Now I try to think of myself as open minded and if you tell me Witten’s recent paper has the potential to “bring it home”, then I’m happy to give it the benefit of doubt, but your description did not sound very much like physics to me, which is probably just my ignorance speaking.
Chern-Simons theory seems interesting. It has popped up in my reading list repeatedly over the years, but is it physics? Is the connection (pun?) from Chern-Simons to physics via BF theory? BF theory always seems “close” to being about physics. I remember many late nights in grad school with my mind swirling thinking about “area flux”, i.e. the flux of some field imposing area on the surface it penetrates and “volume flux” etc. Regge calculus. All super fun stuff and all close to physics in my opinion.
Anyway, if physics is about to make a come back as you suggest, I’ll be happy to watch from here on the sidelines.
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeJul 21st 2010
The opening paragraph is pure rubbish.
Ahm, I’d hope you know what you are talking about when you say this.
-
- CommentRowNumber19.
- CommentAuthorzskoda
- CommentTimeJul 21st 2010
- (edited Jul 21st 2010)
Hm, a discussion which is a bit of detour from the title above (BV-BRST formalism). But in paralellel there is lab activity on BRST stuff! Just to remind you that BRST reduction is another side of the coin of mathematician’s semiinfinite cohomology for which I created the entry today; Koszul duality being one of the building blocks both for this and currently changing entry Chevalley-Eilenberg algebra. I wish somebody will systematically relate these nlab entries soon.
As far as the discussion above is concerned, FQFT is a fantastic insight into topological theories but for general QFTs we need to go back to analysis and geometry, beyond the topological terms (say in semiclassical expansion) which are of higher categorical nature, as most of the topology is.
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeJul 21st 2010
AQFT is a fantastic insight into topological theories
What do you mean by that? One thing that AQFT (in the sense of Haag-Kastler local nets) does not apply to is TFTs. It applies to QFT on Minkowski space or, with some modifications, on Lorentzian spacetimes. Such as the worldsheet of a string.
-
- CommentRowNumber21.
- CommentAuthorzskoda
- CommentTimeJul 21st 2010
- (edited Jul 21st 2010)
Sorry, I meant FQFT !!
I am not versatile in your notation though I spent much of my time and therefore risk my career following your approach last two years. I correct/edited.
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeMar 3rd 2011
I have tried to clean up BRST-BV formalism a little.
And then I finally added some genuine content: in the section on homotopical symplectic reduction I state the main definitions and theorems. But formatting still a bit rough. Can try to polish later.
-
- CommentRowNumber23.
- CommentAuthorUrs
- CommentTimeMar 4th 2011
I redid much of the Idea-section at BRST-BV formalism, trying to reduce repetition and add more information. i think it is better now than it was before,
-
- CommentRowNumber24.
- CommentAuthorzskoda
- CommentTimeMar 4th 2011
In Kontsevich’s approach to renormalizaton via OPE’s the sheaf of local fields also forms a D-module and the sections of that sheaf tensored with the volume form (properly shifted in degree) form an -algebra. In the case of trasnlationally invariant theory he gets an algebra over a little disk operad in the appropriate dimension.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeMar 8th 2011
- (edited Mar 8th 2011)
I have started a section Lagrangian BV – the standard construction meant to provide a review and lightweight formalization of the standard story in the literature.
So far I have made it to the point where the antifield-antighost Tate-like resolution has been defined. Running out of steam for the moment.
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeMar 17th 2011
added to BRST-BV formalism the pointer to the reference by Costello-Gwilliam where they indicate how the BV-complex ought to be thought of as a derived critical locus, and added a pointer to the page where I am trying to work out some details.
-
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeJun 16th 2011
I have added to BV-BRST formalism a link to Frederic Paugam’s latest: Homotopical Poisson reduction of gauge theories .
-
- CommentRowNumber28.
- CommentAuthorUrs
- CommentTimeJun 16th 2011
added that reference also to Berezin integral and integration over supermanifolds
-
- CommentRowNumber29.
- CommentAuthorzskoda
- CommentTimeJun 17th 2011
Paugam’s article looks quite readable!
-
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeJun 17th 2011
Yes, I like it a lot. That’s his contribution to our book.
-
- CommentRowNumber31.
- CommentAuthorjim_stasheff
- CommentTimeJul 9th 2012
@Koszul duality being one of the building blocks both for this and currently changing entry Chevalley-Eilenberg algebra. I wish somebody will systematically relate these nlab entries soon.
like several of the comments above, this evokes BFV more than BV formalism
e.g. BFV feature constraints prominently whereas I thought BV was all aboout Lagrangians with symms??
btw, it's hard to search for notation like $T^*[1]M$ or am I just illiterate at seaerchin?
a basic reference would be appreciated -
- CommentRowNumber32.
- CommentAuthorUrs
- CommentTimeJan 23rd 2013
at BV-BRST complex there used to be a paragraph on how over a manifold with a volume form the BV complex of multivectorfields is dual to the deRham complex.
I have reorganized that and then expanded to sections now called
Even though I expanded a good bit the material that used to be there, this still needs further work. But it should be a start. For more see Owen Gwilliam's thesis.
-
- CommentRowNumber33.
- CommentAuthorzskoda
- CommentTimeJul 7th 2015
I have added today’s reference
- Alberto Cattaneo, Pavel Mnev, Nicolai Reshetikhin, Perturbative quantum gauge theories on manifolds with boundary, arxiv/1507.01221
-
- CommentRowNumber34.
- CommentAuthornLab edit announcer
- CommentTimeFeb 13th 2019
-
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeMay 3rd 2021
added pointer to today’s
- Marco Benini, Pavel Safronov, Alexander Schenkel, Classical BV formalism for group actions (arXiv:2104.14886)
-
- CommentRowNumber36.
- CommentAuthorUrs
- CommentTimeJan 29th 2024
added pointer to:
- Maxim Grigoriev, Dmitry Rudinsky, Notes on the -approach to local gauge field theories, Journal of Geometry and Physics 190 (2023) 104863 [arXiv2303.08990, doi:10.1016/j.geomphys.2023.104863]
-
- CommentRowNumber37.
- CommentAuthorperezl.alonso
- CommentTimeJun 6th 2024
pointer
- Pavel Mnev. Lectures on Batalin-Vilkovisky formalism and its applications in topological quantum field theory (2017). (arXiv:1707.08096).
1 to 37 of 37