nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeMar 2nd 2010
started something at Hamilton operator
-
- CommentRowNumber2.
- CommentAuthorTobyBartels
- CommentTimeMar 2nd 2010
I have always seen this in English as Hamiltonian operator. That already redirects to Hamiltonian; I am guessing that you wrote your article in ignorance of the existence of that one.
They did cover basically different ground —classical vs quantum—, so while I've now put it all in one article, I don't intend to imply that you can't split them again. (I wouldn't do that, but I'm not the one writing.) Just make sure that the redirects go where they should. (^_^)
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeMar 2nd 2010
Oh. Thanks, Toby, very good to have you around. Indeed, I missed all that. Thanks.
-
- CommentRowNumber4.
- CommentAuthorIan_Durham
- CommentTimeMar 3rd 2010
I added a quick note about unitaries to this entry. It looks unfinished since I had to run to dinner. I'll clean it up later unless someone else wants to jump in. -
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeMar 3rd 2010
Thanks. So I added to the paragraph that I had written the remark on how this exponential expression that you write is the parallel transport of
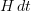 in the case that H is time-independent. More generally the parallel ztransport is given by the path-ordered exponential, which in the physics literature is known as the "Dyson formula".
in the case that H is time-independent. More generally the parallel ztransport is given by the path-ordered exponential, which in the physics literature is known as the "Dyson formula". -
- CommentRowNumber6.
- CommentAuthorIan_Durham
- CommentTimeMar 3rd 2010
Thanks! That's something I actually didn't know. Perhaps I should be embarrassed by this fact, but I have never heard of the Dyson formula. Is this a field theory thing?
I like this site. I learn something new everyday! -
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeMar 3rd 2010
- (edited Mar 3rd 2010)
it might be that people in quantum field theory are more likely to refere to this , but a priori it is just a quantum mechanical thing.
The "Dyson formula" is precisely what mathematicians call "parallel transport".
Some relevant wikipedia entries are Dyson series and method of Dyson series
We should eventually work more of this into the Lab. If you have some time, feel encouraged to go ahead.
-
- CommentRowNumber8.
- CommentAuthorIan_Durham
- CommentTimeMar 4th 2010
Thanks! I just realized that the Dyson series is that part of QED that is insanely accurate. I always knew that QED was the most empirically accurate physical theory to date but never knew that this was the source of that accuracy (which is odd since it's asymptotically divergent).
I've started a page on the Dyson series/formula. Since it's not my strong suit I'm sure someone will need to clean it up.
1 to 8 of 8