nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeMar 5th 2010
- (edited Mar 5th 2010)
edited universal covering space
moved my proof to here that it is the homotopy fiber of the morphism
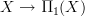 of topological groupoids;
of topological groupoids;then created a new section universal covering spaces in an (oo,1)-topos where I talk about an idea (the evident idea) for what one should say here.
Also propose a definition for Whitehead tower in an (oo,1)-topos this way.
the entry Postnikov tower in an (infinity,1)-category following JL is under way...
-
- CommentRowNumber2.
- CommentAuthorDavidRoberts
- CommentTimeMar 5th 2010
Thanks for that. I noticed I wrote something about doing this a long time ago. -
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeJul 2nd 2017
I have added a little more point-set details to the bginning at universal covering space.
-
- CommentRowNumber4.
- CommentAuthorTodd_Trimble
- CommentTimeJul 3rd 2017
I don’t mean to interrupt Urs’s train of thought (and he should feel free to ignore this while he’s hammering out details), but now returning to this topic about 7 years later, the general abstract construction of universal covering spaces in the context of cohesion seems sort of interesting to me. Part of this is the desire to get free from basepoints, and free from the path-connected assumption on the base space, and free from just groups, passing to groupoids, etc., and connect up with (so-called) “Trimble” -categories…
Here is a diagram I’ve written down on my private web, an abstract construction of what I am provisionally calling the unbiased universal covering space with its projection :
I should explain the notation. We have a cohesive string of adjoints which is just what you expect: is the underlying set functor, and take sets to the associated discrete and codiscrete spaces, and is the (path-)connected components functor. (There are some point-set topology details I’m sliding over for the moment, so that we can consider the big picture.) The map is a counit for , and the map is a unit for . The rest of the notation should be self-explanatory.
Ordinarily, when one constructs a universal covering space, one chooses a basepoint of the base space and looks at homotopy-rel-boundary classes of paths in whose starting point of . The construction above does something similar except that it considers all possible basepoints (hence, “unbiased”). So, whereas in the ordinary construction one chooses an and constructs the space of paths emanating from as a pullback
here we construct a space , the coproduct over all such , as the pullback at the bottom left. The you see at top is similarly formed as a pullback; geometrically it’s the coproduct of spaces where is the space of paths from point to point . Thus would be the hom-set of the fundamental groupoid, and is the coproduct of all hom-sets of (seen as a discrete space). The right map along the top sends a path to its homotopy-rel-boundary class. Thus when we push out to get , we get homotopy-rel-boundary classes of elements of , which is exactly what we want for the unbiased universal covering space. (I’ll continue in the next comment.)
-
- CommentRowNumber5.
- CommentAuthorTodd_Trimble
- CommentTimeJul 3rd 2017
The composite map factors through , and that’s where comes from. (Again, all of this follows I believe from purely formal properties of cohesion.) Of course
is a monoid in the category of endospans (namely the fundamental groupoid), and the span
carries a canonical module structure over this monoid (I guess a right module – whatever it is you call a functor ). If is a left module, then you can form a tensor product or weighted colimit , an object of , in fact when you form that span composition an object of and indeed a covering space over . Then
is the left adjoint in the adjoint equivalence which expresses the fundamental theorem of covering space theory, but expressed in unbiased form.
I’m not sure where to find this in the literature (some authors come close but then pull back, somehow), but the thing I find pleasant is just how formal this is, and how much you can milk on the basis of so little (cohesion plus the topological interval as data). And it hadn’t occurred to me before that the machinery of “Trimble -categories”, following these developments naturally as it were, is maybe best viewed in a cohesive context.
-
- CommentRowNumber6.
- CommentAuthorDavidRoberts
- CommentTimeJul 3rd 2017
You’d want some sort of semi-local simple-connectedness to get local triviality of your , and for the higher stages of the Whitehead tower of , local -connectedness and semilocal -connectedness in order to get a locally constant stack of -groupoids of local sections.
There is work by Jeremy Brazas on the setup when you lose the nice local homotopical conditions, so that is naturally a semitopological group (multiplication is separately continuous in each variable) as a quotient of the based loop space, and you can also put a group topology on it, and get the nice construction of universal “covering spaces” for that framework (fibres are no longer discrete, but one has good lifting properties).
-
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeJul 3rd 2017
Interesting! Fills me with questions.
- Can you then extract a space that’s equivalent to the usual universal covering spaces, instead of a coproduct of a bunch of copies of it, by taking some kind of quotient of ?
- What do you get if you do it all homotopically, i.e. use ʃ instead of and a homotopy pushout instead of a set-pushout?
- What if instead of the pushout, we considered as living over (i.e. ) and take its fiberwise ʃ or ?
-
- CommentRowNumber8.
- CommentAuthorDavidRoberts
- CommentTimeJul 3rd 2017
@Mike Todd has explained this construction before, but not using formal cohesion. Essentially any two copies of a universal cover of a component corresponding to basepoints get identified as there is an arrow between them in . A homotopy pushout would remember which arrow one is using to identify these two covering spaces.
Note that Ronnie Brown would be happy to only go halfway and choose a basepoint in each path component of , but this does away with that by using every single point, then gluing them all back together. It’s really very nice!
-
- CommentRowNumber9.
- CommentAuthorMike Shulman
- CommentTimeJul 3rd 2017
But the pushout all happens over the bottom copy of , so it seems to me that it can’t identify things in one component of with another?
-
- CommentRowNumber10.
- CommentAuthorDavidRoberts
- CommentTimeJul 3rd 2017
That map looks wrong to me. Where does it come from?
-
- CommentRowNumber11.
- CommentAuthorDavidRoberts
- CommentTimeJul 3rd 2017
- (edited Jul 3rd 2017)
(duplicate)
-
- CommentRowNumber12.
- CommentAuthorUrs
- CommentTimeJul 3rd 2017
- (edited Jul 3rd 2017)
Mike, the version in -cohesion is what we have in the Lab entry since rev 6 in 2010: the universal covering space is the homotopy fiber of
over any point (if is connected).
(As one runs through the truncation degree here, one obtains the whole Whitehead tower. This is something that David Roberts and myself made notes about years ago at Whitehead tower in an (infinity,1)-topos. Looking back at it, it could do with some polishing.)
If we don’t like to choose a point, we could instead take the homotopy fiber product with (the points-to-pieces transform). This would give the -many-copies-version of the covering space which Todd is considering above.
In the entry instead the perspective is taken that one takes the fiber product along a choice of section of the 0-truncation. This is not as bad as it sounds, since this section is essentially unique.
But I am inclined to view this as the pullback along something like the “smallest 1-epimorphism out of a 0-truncated object into .” I wish I had a solid general definition of what this should be, because something similar happens in the definition of ordinary differential cohomology:
There we form the homotopy fiber product of a canonical map along something like the “smallest 1-epimorphism-when-evaluated-on-manifolds out of a 0-truncated object”, namely the morphism (from closed differental -forms to the coefficients for degree real cohomology, which is an epimorphism when evaluated on manifolds (or anything smooth with a partition of unity) by the de Rham theorem).
So it seems a common theme that we want to take homotopy fibers of morphisms into some -stack by choosing a smallest 0-truncated object that hits all the connected components of the thing we are pullback back over, at least after evaluating everything on some prescribed class of objects. I keep wanting to have a good general formalization of this rough idea. It might be the answer to some other open problems that I have.
-
- CommentRowNumber13.
- CommentAuthorDavidRoberts
- CommentTimeJul 3rd 2017
This is not as bad as it sounds, since this section is essentially unique.
its mere existence is unique, but it can have many automorphisms!
-
- CommentRowNumber14.
- CommentAuthorTodd_Trimble
- CommentTimeJul 3rd 2017
Guys, thanks very much for your interest and questions! I’m going to be very busy today with other things, but I’m looking forward to getting back to this soon, hopefully by sometime tomorrow. I can tell I’m going to learn a great deal from this, and I’m sure to have questions in return.
I did want to address David’s question in #10 about , which is induced from the map . Set-theoretically it’s supposed to take an equivalence class of paths to . I think it’s well-defined because two paths map to the same in iff when we regard as belonging to (remember that set-theoretically is an identity because it’s a pullback of the set-theoretic identity map on the left), we have : that only happens if (call it ) and (call it ) and there’s a path between in (homotopy-rel-boundary). Anyway, we do have , so is well-defined.
-
- CommentRowNumber15.
- CommentAuthorDavidRoberts
- CommentTimeJul 3rd 2017
Hmm, so you do have a disjoint union of simply-connected covering spaces, one for each point of the space? To my mind, a universal covering space of a disconnected space should induce an isomorphism on . But perhaps that’s just experience with pointed covering spaces talking…
-
- CommentRowNumber16.
- CommentAuthorMike Shulman
- CommentTimeJul 3rd 2017
Thanks Urs! Do you think that can be made to coincide formally with Todd’s definition?
This is not as bad as it sounds, since this section is essentially unique.
its mere existence is unique
… assuming the axiom of choice in the discrete world (right?). (-: Otherwise it might not exist at all. In fact, if sets cover fails, there may not be any epimorphism to an object out of a 0-truncated one.
-
- CommentRowNumber17.
- CommentAuthorDavidRoberts
- CommentTimeJul 3rd 2017
@Mike
assuming the axiom of choice in the discrete world (right?)
of course, and that’s a reason to use the cohesive treatment over the version that assumes one has a section of !
-
- CommentRowNumber18.
- CommentAuthorTodd_Trimble
- CommentTimeJul 3rd 2017
David: yes. And you raise a good point. I’d like to mull over that further…
-
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeJul 3rd 2017
- (edited Jul 3rd 2017)
I have written out now the abstract argument that the definition in cohesive homotopy theory comes out right, this is now the first part of the section (now) titled Universal covering space – In cohesive homotopy theory.
The previous argument that used to be in the entry (now the second part of that section, not notationally harmonized yet), argues that the homotopy fiber of the morphism from to its fundamental groupoid, both regarded as topological stacks, canonically yields the classical construction via homotopy classes of paths, the way Todd is discussing above. For this to be a special case of this abstract construction one needs a result, namely that the shape modality is represented by a “path -groupoid”.
This is true in “Euclidean topological infinity-groupoids” at least, due to a result that Dmiti Pavlov has announced long ago, following a similar result by Bunke-Nikolaus-Völkl. I am recording this now at shape via cohesive path ∞-groupoid.
One would like this to be true also over the -cohesive site of locally contractible topological spaces (or at least over the 1-cohesive site of locally simply connected topological spaces), but I don’t know if it is. Somebody should think about this!
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeJul 3rd 2017
- (edited Jul 3rd 2017)
Regarding choice: Right, I am tacitly assuming choice in the base topos.
From the discussion of the sharp modality as the Aufhebung of the initial opposition (here), with its minimal solution necessarily being Boolean (this remark) I grew fond of the idea that it is quite natural to assume the base of a cohesive theory to be classical. I might go as far as feeling that this neatly captures the whole dichotomy between classical and constructive logics: we do want both, but the former precisely only in the base of discrete types, while the latter in the full theory of cohesive types.
In any case, if we don’t allow ourselves to choose single basepoints at all, then I don’t see how to get rid of the the spurious copies of the universal covering space.
-
- CommentRowNumber21.
- CommentAuthorMike Shulman
- CommentTimeJul 3rd 2017
I would be somewhat doubtful that local contractibility is enough, but I could be wrong. My hope would instead be that the identification can be proved internally from the real-cohesion axiom.
-
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeJul 4th 2017
Do you know if the internal real cohesion satisfies the property that shape preserves pullbacks over discrete types?
-
- CommentRowNumber23.
- CommentAuthorDavid_Corfield
- CommentTimeFeb 9th 2021
I see Peter Scholze returned to an MO question on universal covers from a condensed mathematics perspective here. Presumably cohesive homotopy types can do a similar job.
-
- CommentRowNumber24.
- CommentAuthorDavid_Corfield
- CommentTimeFeb 9th 2021
- (edited Feb 9th 2021)
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeDec 25th 2021
added pointer to
- William S. Massey, Chapter 5, Section 10 of: Algebraic Topology: An Introduction, Harcourt Brace & World 1967, reprinted in: Graduate Texts in Mathematics, Springer 1977 (ISBN:978-0-387-90271-5)
for an original reference (maybe the construction via equivalence classes of based paths originates with the discussion on p. 175 here?)
and pointer to
- Tammo tom Dieck, Section I (10.13) of: Transformation Groups, de Gruyter 1987 (doi:10.1515/9783110858372)
for generalization to equivariant homotopy theory.
-
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeDec 26th 2021
- (edited Dec 26th 2021)
prodded by the exchange at “fundamental theorem of covering spaces” (here)
have added pointer to definition of universal covering spaces
in cohesive homotopy theory
- Def. 3.8.10 in dcct
and explicitly so in cohesive homotopy type theory:
- Felix Cherubini, Egbert Rijke, Def. 8.5: Modal Descent, Mathematical Structures in Computer Science (2020) (arXiv:2003.09713, doi:10.1017/S0960129520000201)
-
- CommentRowNumber27.
- CommentAuthorDmitri Pavlov
- CommentTimeNov 17th 2023
Added:
A detailed treatment is available in
- Nicolas Bourbaki, Topologie Algébrique, Chapitres 1 à 4, Springer, 2016. doi:10.1007/978-3-662-49361-8, ISBN 978-3-662-49361-8.
1 to 27 of 27