nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
Atrium > Mathematics, Physics & Philosophy: principal bundles with a connection as a stack?
Bottom of Page1 to 26 of 26
-
- CommentRowNumber1.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 7th 2010
- (edited Mar 7th 2010)
this is related to the thread on flat connections I'm occasionally posting here on the forum and trying to develop in my area, but I prefer making an independent discussion of this since it could be of a wider interest.
locally, a -principal bundle with a connection is a -valued 1-form on an open subset of a manifold . but can also be seen as a functor , where is the groupoid of 1-paths. so, if we consider all possible -connections on , we are defining a map
this has at all the aspect of a prestack (pre-1-stack, I mean) on the site of open subsets of , so I can think to stackify it to obatin a stack whose global sections are principal -bundles on with a -connection. indeed, to give global sections I have to give descent data, and so, locally on double intersections a natural transformation of functors (a gauge equivalence), in such a way that on triple overlaps everything commutes (the cocycle condition).
this point of view seems to imemdiately generalize to higher groups, giving an higher stack of higher principal bundles with connections, while the local description in terms of differential forms should be related to a de Rham type description of nonabelian differential cohomology. -
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeMar 8th 2010
That's true, yes.
-
- CommentRowNumber3.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 9th 2010
- (edited Mar 9th 2010)
fine. so I guess that stackification of gives principal -bundles (here is the groupoid of 0-thin paths, so, concretely, the discrete groupoid on the set ), and that the natural inclusion corresponds to the natural forgetful morphism "-bundles with a connection" "-bundles". looking this the other way round, endowing a given -bundle described by some cocycle with a -connection, amount to lifting a morphism from to and so to refine the given cocycle to a differential cocycle.
what I like of this path groupoids point of view is that one talks of connections without differenial forms. moreover this way of looking at connections seems closer to the original idea of a conncetion on a bundle as something relating fibres at different point; what one does is to formalize the naive picture by using categorical language. and in my point of view this is more natural than translating everything in the language of differential forms. not that I'm sayng that th differential forms formalization is not important. I do think it is an equally important point of view as the functorial one (how could it not be so? they are equivalent :-) and there has been a time when the only available language to properly formalize the naive notion has been that of differential forms), but I feel the paths point of view is better in answering the socratic question What is a connection?
I'm sayng this since (as you know since you read my posts..) I'm currently obsessed with the follow-up question. namely, What is curvature? Urs gives a beautiful answer in terms of differential forms (Chevalley-Eilenberg algebras, Weil algebras, and all that), but I fail in understanding this on the paths side, where instead I expect there should be a natural answer. the only thing I've been clearly able to see so far is the following:
to a principal -bundle with a connection is associated a 2-form with coefficients in . what is crucial is that is globally a 2-form, not only locally so. this means that, if I want to think of as something like a 2-connection on some principal -bundle, then this will be a trivial -bundle. that is, my ambient is not anymore, is something else.
Extremely confused... I apologize for this. -
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeMar 9th 2010
fine. so I guess that stackification [,,,]
Yes, that's rigtht.
what I like of this path groupoids point of view is that one talks of connections without differenial forms.
Yes!
What is curvature?
But we said this before: curvature for a transport
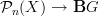 is some transport
is some transport 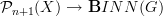
-
- CommentRowNumber5.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 9th 2010
I know.. but I know this only a posteriori. I mean, going through the differential forms definition of curvature, and then interpreting this back in terms of -dimensional transport. But I'm still unable to see this directly. And, most of it, I'm still unable to see a priori that curvature is a globally defined 2-form, despite a connection is so only locally.
I know I'm very confused about all this, and apologize for posting such confused stuff.. -
- CommentRowNumber6.
- CommentAuthorUrs
- CommentTimeMar 10th 2010
- (edited Mar 10th 2010)
But I'm still unable to see this directly. And, most of it, I'm still unable to see a priori that curvature is a globally defined 2-form, despite a connection is so only locally.
Okay, so what you need is the full story of how one derives this.
Let's do the simpler case first, where the coefficient object is a group object. Recall the abstract definition of "abstract de Rham cohomology" not in terms of differential forms, but just in terms of flat oo-bundles whose underlying oo-bundle is trivial. (See the diagrams there.)
Then it is a theorem that we have a fibration sequence
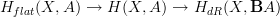 .
.This allows us to define non-flat differential cohomology with coefficients in A to be the homotopy fiber of
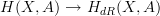 over the given curvature class. This curvature class is by definition of
over the given curvature class. This curvature class is by definition of 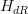 globally defined. Have a look at the link for the case of groupal coefficients.
globally defined. Have a look at the link for the case of groupal coefficients. -
- CommentRowNumber7.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 10th 2010
- (edited Mar 10th 2010)
Wow, that's brilliant! absolutely brilliant!
yet, I feel there's still something that can be said on the very final part, where Chevalley-Eilenberg and Weil algebras appear.
namely, you know the appearance of starting with a classical connection on a principal -bundle via the cone construction seems a bit forced to me, and I'd like to see directly appearing e.g. when I deal with a functor . And maybe I finally see it: taking the boundary of a 2-morphism in gives a loop in ; this is a morphism in and so we have a map from 2-morphisms in to . since 1-morphisms in are morphisms in , we also have a map from at the level of 1-morphisms. and when works out the definition, one sees that these two maps are precisely a 2-functor . moreover, since the functor at the level of 2-morphisms has been defined taking a boundary and so actuall going to 1-morphisms, this functor does not know whether 3-simplices are 2-thin or not! so there is no obstruction to lifting it to a functor , and, more in general to a functor : it is a flat -connection!
this seems now so clear to me I feel shame for having not seen it for such a long time :( -
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeMar 10th 2010
and, more in general to a functor \Pi(X)\to \mathbf{B} INN(G): it is a flat \mathbf{B} INN(G)-connection!
Yes, that's the idea, exactly.
-
- CommentRowNumber9.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 10th 2010
so, let me say it once again to see if I finally got it: given an n-group there is a unique way to extend it to an (n+1)-group in a way compatible with the boundary map from the (n+1)-simplex to the diagram given by its n+2 boundary n-simplices. this unique way is the INN construction.
and, when applied to representations of n-paths groupoids, this is curvature. -
- CommentRowNumber10.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 10th 2010
on second thought, I was too rough in saying that this unique way is the INN construction. what I should have said is that this unique way is a INN-type construction. indeed, even in the case of a 1-group , one can build an INN-type extension for any normal subgroup of . so provides a good target, but the actual image of in can be smaller. for instance, if the given 1-connection is flat, then one is dealing with the 2-group built from by the INN-construction with , and this is the same thing as .
this looks like a reduction of structure group in classical principal bundles theory. so its obstruction should be detected by some cohomology class. so it seems to that flatness question could be rephrased as follows: given a -valued -connection, which is the obstruction to reduce the structure (n+1)-group for the associated -connection to the group ? one can pose this question more in general and ask for the obstruction to reduce the associated connection to the (n+k)-group . taking and one finds abstract de Rham cohomology as Urs develops it. -
- CommentRowNumber11.
- CommentAuthorTim_Porter
- CommentTimeMar 10th 2010
There are very close connections with reduction of structure group. In fact in non_abelian cohomology where the construction INN(G) sort of originates is is usual (following Dedecker) to use a 2-group as coefficients or rather the corresponding crossed module in that setting. I have been trying to look at Turaev's homotopy quantum field theory from this point of view, but I find it quite hard going. In algebraic geometry some useful ideas have been emerging with work by Aldrovandi and Noohi on Butterflies (which in n-lab speak are ......? I leave someone else to say because I always choose the wrong term!) Their stuff would seem to be connected with what you are talking about.
-
- CommentRowNumber12.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 10th 2010
thanks for the reference!
in the menawhile I was thinking to this: if one systematically uses the adjoiness , then one should be able to write everything at abstract de Rham cohomology directly in terms of the morphism of oo-stacks rather than in terms of the represented functor. the two formulations should be equivalent by yoneda, but maybe avoiding the 's and the can make a few point of the exposition clearer.
(just a suggestion. Urs, in case you agree I can attemp a rewriting in this direction in my area, so that if you like it you can copy and paste) -
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeMar 10th 2010
- (edited Mar 10th 2010)
Butterflies (which in n-lab speak are ......?
a butterfly is a butterfly is a butterfly... :-)
Butterflies are just a way to present morphisms in
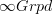 between one-object 2-groupoids.
between one-object 2-groupoids. -
- CommentRowNumber14.
- CommentAuthorDavidRoberts
- CommentTimeMar 11th 2010
Well a butterfly is closely related to a saturated anafunctor internal to (at least) a semiabelian category - actually more like the bibundles/Hilsum-Skandalis morphisms internal to such. But butterfly is a good term (and I vaguely recall Jean Pradines used the term before Noohi anyway).
Recall that BINN(G) -> BG is the universal cover (B here is delooping, not classifying space), and the fact it is the 2-group of inner automorphisms is not automatic. This surprised me, when Urs and I wrote our paper on the analogous situation for G a strict 2-group. I was only looking at 2-connected covers, originally. -
- CommentRowNumber15.
- CommentAuthorTim_Porter
- CommentTimeMar 11th 2010
- (edited Mar 11th 2010)
Pradines certainly used the term but I am not sure it is in exactly the same context.
I did not know that there was an entry on butterflies!
There is a second part of Butterflies: ArXiv 0910.1818. I have added a link to the entry.
-
- CommentRowNumber16.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 11th 2010
<blockquote><bockquote >I was only looking at 2-connected covers, originally. </blockquote><br /><br />this is interesting, since it perfectly agrees with the geometric picture I was trying to describe in the posts above: functors <latex >\mathcal{P}_1(X)\to \mathbf{B}G</latex> lift to functors <latex >\mathcal{P}_2(X)\to Something</latex>, and this something one has to expect to be the 2-connected cover of <latex >\mathbf{B}G</latex>. <br />it is precisely what I was trying to mean by saying I didn't like the appearance of <latex >INN(G)</latex>, and would have liked a more geometric description on the first spot, which then one could prove to be explicitly given by the INN construction.<br /><br />thanks a lot :-)</bockquote> -
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeMar 11th 2010
There is a second part of Butterflies: ArXiv 0910.1818. I have added a link to the entry.
Thanks. I added a remark on terminology to this at butterfly and then added the reference also to principal 2-bundle.
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeMar 11th 2010
By the way: somebody wrote at principal 2-bundle that while that concept is more general than that of gerbe, that of gerbe could "easily be generalized to match".
I am not so sure about this. If you start generalizing the simple statement "locally non-empty and connected stack" such that it describes sections of general 2-bundles, you have to say things that effectively make you say "principal 2-bundle" and no longer say "gerbe".
-
- CommentRowNumber19.
- CommentAuthorDavidRoberts
- CommentTimeMar 11th 2010
As an example, every 2-covering space Z -> X, where X is a space, factors as Z -> Z' -> X where Z -> Z' is a bundle gerbe (but much more general than Murray's definition) and a covering space Z' -> X. So I expect a general 2-bundle to be a gerbe over some suitable cover, like the total space of a principal bundle. -
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeMar 11th 2010
So I expect a general 2-bundle to be a gerbe over some suitable cover, like the total space of a principal bundle.
Indeed. There is described in the second section at string structure. In my last article with Stasheff and sati we call this "local semi-trivialization": instead of pzulling back the 2-bundle to its own total space where it trivializes, one pulls it back just to a covering spaces, where it jusgt b ecomes a bit simpler.
-
- CommentRowNumber21.
- CommentAuthorDavidRoberts
- CommentTimeMar 12th 2010
At least in my set-up, it's a bit simpler: one doesn't need to pullback at all. Note that in the case of the 2-connected 2-covering space this is a manifestation of the bottom two steps of the Whitehead tower. -
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeMar 12th 2010
At least in my set-up, it's a bit simpler:
Even simpler?!
Can you write into some entry precisely what you have in mind?
-
- CommentRowNumber23.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 12th 2010
this reminds me of some discussion we had on nonabelian group cohomology. also there, there is an INN-construction which a priory may seem (at least to me) arbitrary, and I would prefer thinking of higher cohomology with coefficients in as cohomology with coefficients in the higher connected covers of . so, I like very much David sayng (if I'm not misunderstanding) that the two points ov view are actually equivalent.
also, from the higher connected covers point of view the abelian case would be special in that the 1-connected cover of an abelian lie group is contractible, and so Whitehead tower is trivial after the first step.
by the way, is not the 2-group called AUT(K) in nonabelian group cohomology what in other places has been called INN(K)? or am I missing something? -
- CommentRowNumber24.
- CommentAuthorDavidRoberts
- CommentTimeMar 12th 2010
@domenico
INN(K) is most certainly not the same as AUT(K): INN(K) is transitive as a groupoid, but AUT(K) has as set of connected components the group Out(K) = Aut(K)/Inn(K). I'm going to be a bit lazy and say: for the discussion of the relation between the two see Urs and my paper.
@Urs,
I mean it is simpler in that the projection map factorises through a covering space, which is the orbit space of the groupoid which is the total space of the 2-covering space.
I would put in a page on 2-covering spaces, but I can't edit at the moment. -
- CommentRowNumber25.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 12th 2010
- (edited Mar 12th 2010)
@david
thanks. sure AUT(K) and INN(K) are not the same, it's me that in reading the crossed module description at nonabelian group cohomology got confused between the two. but now I've checked and I was clearly wrong. (the fact is in the crossed module description INN has , whereas AUT has , so I messed them up... :-( ) -
- CommentRowNumber26.
- CommentAuthorDavidRoberts
- CommentTimeMar 13th 2010
Yeah, I got somewhat confused when I started with crossed modules, as no one had a name for INN(K) at the time. Then there was trying to figure out what acted on what when considering the associated 2-group (Aut(K) and K act on each other for different reasons!)
1 to 26 of 26