Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory internal-categories k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes: fibration sequence

Bottom of Page

1 to 4 of 4

  1.  
  1. in fibration sequence, changed the second diagram after "But the hom-functor has the crucial property..."

    please someone check with the previos version to see if my correction is correct.
    • CommentRowNumber2.
    • CommentAuthorUrs
    • CommentTimeMar 11th 2010

    Hm, my impression is that you changed one correct expression to an equivalent correct expression.

    But for the argument to follow the first correct expression is the one needed! On the other hand, this follows indeed using your correct expression.

    So I guess we want both expressions. I have now implemented that. I have also renamed that object C into K, since the ambient category is already called C and so there was a bad notation clash. Probably that didn't help to clarify the situation. Please have another look and see if it is better now.

    • CommentRowNumber3.
    • CommentAuthorUrs
    • CommentTimeMar 11th 2010

    Hm ,wait, actually you are right and I am wrong in that the expression 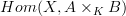Hom(X, A \times_K B) is needed in the following, and 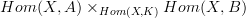Hom(X,A) \times_{Hom(X,K)} Hom(X,B) is not. That latter is needed to see things like 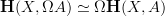\mathbf{H}(X, \Omega A) \simeq \Omega \mathbf{H}(X,A) and the like.

    Allright, so thanks for catching that.

  4. what I meant is that if one writes the diagram with in the upper right corner, then this is by definition an homotopy pullback, so it is not immediately clear what one means by saying that is exact. I think now it looks better, but I edited it once again in order to make it even mor explicit: exactness of is ubiquously used in npov on cohomology, so let us state in it the clearest possible way... :-)

    please when you have time have a look

1 to 4 of 4

  1.