nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 12th 2010
there is something not convincing me in the definition of twisted cohomology. I'm pretty sure the definition is given this way in order to reproduce the classical notion, but when one directly reads the general definition given in a (oo,1)-topos, this looks a bit odd.
namely, data are given as follows:
- an (oo,1)-topos H
- a fibration sequence A --> C --> B in H;
- an object C of H;
- an element c in H(X,B) (the twisting cocycle).
then the the c-twisted A-cohomology of X is defined as the homotopy pullback of the diagram H(X,C) --> H(X,B) <--- *, where the map on the right is the cocycle c.
so the question is: which is the role of A in this construction? writing H[c](X,A) for the construction above seems to be just a way to remember what one would get in case c is the trivial cocycle given by H(X,*-->B). also, H[c](X,A) seems to have no kind of functoriality.
on the other hand, considering all twisted cohomologies at once seems to be something much more well behaved, something like a fibrant replacement of
H(-,C) --> H(-,B) (not that I know what this should exactly mean, it's worth I have a look at global model structure on functors, now...) -
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeMar 12th 2010
the A is implicit. You can read it as being defined as the homotopy fiber of B -> C . The point of it is just to record which cohomology is being twisted.
-
- CommentRowNumber3.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 12th 2010
- (edited May 4th 2010)
ok. so it is actually as I was saying:
a way to remember what one would get in case c is the trivial cocycle
by the way, do you think the fibrant replacement suggestion can somehow be formalized into something meaningful, or you feel it is a completely wrong idea?
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeMar 12th 2010
Sorry, I am not following that fibrant replacement remark. Could you say again in more detail what you have in mind?
-
- CommentRowNumber5.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 12th 2010
well, I was thinking that a way to computing homotopy fibers of a morphism Y --> Z is to replace it with a fibration and then take actual fibers of this. so taking homotopy fibers of H(X,C) --> H(X,B), i.e. twisted cohomologies, is the same as taking actual fibers of a fibrant replacement of this morphism. therefore, I thought, the naive idea of considering all twisted cohomology at once corresponding to consider the fibrant replacement of H(-,C) --> H(-,B).
here comes a technical point I'm not sure about: does "C --> B is a fibration" imply "H(-,C) --> H(-,B) is a fibration"? -
- CommentRowNumber6.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 15th 2010
let me try say things in a different way. in the npov, cohomologies are just oo-categorical hom spaces in an (oo,1)-topos H. so they are just "values" of representable functors, and since in a sense a functor is more interesting than the collection of its values, cohomology theories "are" representable functors, taht is, by Yoneda, they are just objects of the (oo,1)-topos H one started with. so, said in an very extreme way, in the npov, cohomology does not exist.
there will be more and lessintresting cohomology theories, depending on how "interesting" is the object representing them, but it seems that every classical construction in cohomology can be read as "take a few objects in H, make ome natural contruction out of them, then consider the functor represented by this".
the only construction I've seen which seems to escape this paradigm is twisted cohomology: the choice of a twisting cocycle involves also the source space and not only the target space (the coeffcients of cohomology). that's why I feel uneasy with it and would rather consider all twists at once as the fundamental object. the trivial twist is a different issue: that corresponds to a distinguished point in the coefficients, and does not depend on the source object. this makes it of a really different nature with respect to other twists, at least at this level of my understanding the question. -
- CommentRowNumber7.
- CommentAuthorDavidRoberts
- CommentTimeMar 15th 2010
One thing to keep in mind is that the idea of a universal case for twisted cohomology doesn't really exist in the usual sense. For example, the K-theory of a space, twisted by a PU-bundle on that space, is not just represented by the classifying space of K-theory, but also involves a classifying map for the PU-bundle. This may (or may not! I'm not sure) be pulled back from a universal such bundle on the classifying space of K-theory, which is pulled back along the canonical map KU -> K(Z,3) = BPU (not sure if the notation KU is correct, but you know what I mean) which is a Postnikov section, and the canonical PU bundle over BPU. Anyway, you probably know all this, it just helps me to get a handle on what you're talking about
-
- CommentRowNumber8.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
well, I was thinking that a way to computing homotopy fibers of a morphism Y --> Z is to replace it with a fibration
Ah, I see. Yes, that's right. This is explained at homotopy pullback: we may compute the homotopy pullback of a diagram
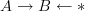 by computing the ordinary pullback of a weakly equivalent diagram that satisfies some nice properties. A sufficient property is: all three objects are fibrant and at least one of the morphisms is a fibration. In that case the ordinaty pullback is guaranteed to be weakly equivalent to the homotopy pullback
by computing the ordinary pullback of a weakly equivalent diagram that satisfies some nice properties. A sufficient property is: all three objects are fibrant and at least one of the morphisms is a fibration. In that case the ordinaty pullback is guaranteed to be weakly equivalent to the homotopy pullback -
- CommentRowNumber9.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
said in an very extreme way, in the npov, cohomology does not exist.
Well, it is an extreme case of the general principle that the nPOV simplifies concepts. Here it may be surprising just how simple the concept becomes, but it is still of interest to have the simple concept and all its nontrivial specific incarnations.
-
- CommentRowNumber10.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 15th 2010
- (edited May 4th 2010)
absolutely! and I love cohomology in all of its specific incarnations, an the unifying npov on them at the same time! what I wanted to stress is how much twisted cohomology seems to fail (at least at first sight) to fit the simple concept. not that twisted cohomology is something difficult, but it is at first sight something really different from other cohomologies. as David says,
One thing to keep in mind is that the idea of a universal case for twisted cohomology doesn’t really exist in the usual sense.
maybe it is just a matter of names.. one day something has been called twisted cohomology since its by hand construction looked like cohomology, but should have the hom-space pov on cohomoloy been more standard that day, maybe a different name would have been chosen, and this thread would not exist :-)
yet, I still try to think for a while to what universal twisted cohomology could be, before giving it up. and, ad David points out, I’ll have to test everything on twisted K-theory first.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
how much twisted cohomology seems to fail (at least at first sight) to fit the simple concept.
well, it's more complicated, but still surprisingly simple, to my mind: we identify cohomology with hom-complexes. Then we are naturally interested in understanding morphisms of hom-complexes. These in turn are to a large degree characterized by their homotopy fibers. Which is the home of twisted cohomology. That is pretty nice, i think.
-
- CommentRowNumber12.
- CommentAuthorTim_Porter
- CommentTimeMar 15th 2010
Is it worth saying that there may be sometimes a need to calculate some cohomology 'class'. The idea that cohomology (in the classical topological case) is the spectrum that represents it is not new (in that case) but what does it mean to calculate the cohomology of a 'space'? Surely the npov sheds light on the problem but pushes the work to something like the job of calculating homotopy classes of maps, and that is highly non-trivial. Similarly saying an oo-groupoid is a Kan complex is enlightening and at the same time, means you still have to work out how to 'calculate' with it. Perhaps extracting information from things like this is the next set of challenges for the npov!
-
- CommentRowNumber13.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
Perhaps extracting information from things like this is the next set of challenges for the npov!
I see on the one hand the nPOV that tells you what to do, and on the other hand the concrete work you have to do it. The nPOV is not meant to make all computation superfluous. It is meant to organize it neatly. It provides a guide that ensures that if one has to compute something, at least one is sure about the nature of what it is one is computing. You still have to compute it, though. That's how I see it.
-
- CommentRowNumber14.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 15th 2010
- (edited May 4th 2010)
Then we are naturally interested in understanding morphisms of hom-complexes.
Exactly! one wants to study the morphism A –> B in H, and this is the same as studying the morphism H(-,A) –> H(-,B), and a lot of information can be read by studying the (homotopy) fibers of H(X,A) –> H(X,B) as X varies. I’m just saying that a ’single’ homotopy fiber is not interesting, is the ’collection’ of all homotopy fibres that matters.
when B is pointed, the morphism A –> B picks out a distinguished fibration sequence and we have (non-twisted) cohomology with coefficients in the (homotopy) fiber. but if we forget about the distinguished point in B, then what we get looks rather like a ’bundle’ of cohomologies over B: for every X-point of B, i.e., every cocylce c in H(X,B) there is the homotopy fiber of A –> B over that point. a couple of posts ago I was suggesting to think of this homotopy fiber as the ordinary fiber of a fibrant replacement, but now I see that the only fiber ’meaningful within (oo,1)-topos description of cohomology’ would be a homotopy fiber, so let us directly say fiber: the ’collection’ of all twisted cohomologies of X (with coefficients in the fiber of A –> B over the distinguished point of B), is the collection of all fibers of the morphism A –> B, i.e., it is the morphism A –> B itself.
in other words, in the npov, twisted cohomology does not exist. :-P
just joking here. but seeing things this way I now think the identity B –> B seen as a twisting cocycle for the twisted cohomology of B could have some relevance to the above.
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
Ah, now I see what you mean. Yes, I guess I very much agree with this.
So the total twisted cohomology is the homotopy pullback of the morphism
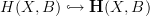 that picks for each cohomology class in
that picks for each cohomology class in 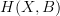 a (any) cocycle representative. The homotopy pullback of that along
a (any) cocycle representative. The homotopy pullback of that along 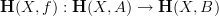 is the total twisted cohomology specified by the morphism
is the total twisted cohomology specified by the morphism 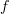 . It comes with two projections: one to the underlying
. It comes with two projections: one to the underlying  -cocycles, one to the twisting classes in
-cocycles, one to the twisting classes in 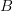 -cohomology.
-cohomology. -
- CommentRowNumber16.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 15th 2010
isn't this the graph of ? -
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
isn't this the graph of f?
I see what you mean. it is something like that, yes. Maybe closer to the graph of
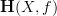 for fixed X.
for fixed X. -
- CommentRowNumber18.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 15th 2010
not sure I want to fix X. let us take the graph of f instead (as the homotopy pullback of f:A --> B <-- B :id ), and then use the exactness of , instead. -
- CommentRowNumber19.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
- (edited Mar 15th 2010)
I see what you are getting at, but the homotopy pullback of an identity is trivial: an equivalence.
In this business
 does play a role more than just being a spectator. It determines which twisting cocycles are available. The notion of "twisting cocycle" does not exist without having a domain.
does play a role more than just being a spectator. It determines which twisting cocycles are available. The notion of "twisting cocycle" does not exist without having a domain.But let me think what we can do to get what you want to get...
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
So suppose we could choose representatives of cocycles functorially as
 changes, so that we would get a transformation
changes, so that we would get a transformation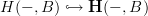
where
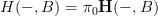 . If we could choose this, then I suppose we would take the homotopy pullback in the oo-category of oo-presheaves on
. If we could choose this, then I suppose we would take the homotopy pullback in the oo-category of oo-presheaves on 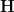 , yes, of the diagram
, yes, of the diagram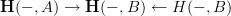
which of course you are entitled to write simply as
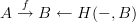
Now I am not sure: do we expect to be able to choose cocycle representatives functorially? Hm...
-
- CommentRowNumber21.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 15th 2010
- (edited Mar 15th 2010)
no, I don't think so. therefore I would directly work with , and would add a projection to only in the end. -
- CommentRowNumber22.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
- (edited Mar 15th 2010)
Yeah, but the pullback of the identity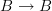 will be an identity/equivalence. So that does not capture the information that I suppose you would want to capture.
will be an identity/equivalence. So that does not capture the information that I suppose you would want to capture.
-
- CommentRowNumber23.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 15th 2010
I know. This is what I meant by saying that the collection of all twisted cohomologies coming from is the morphism itself. in my point of view, the collection of all twisted cohomologies is 'a way of looking at ' -
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeMar 15th 2010
Okay, sure.
-
- CommentRowNumber25.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 16th 2010
I'm now thinking it would not be bad to borrow some language from classic algebraic gometry: if is the functor of points of , then elements of are the -points of , and twisted cohomology is the fiber of a morphism over a point of . If is pointed, then for any there is a unique distinguished -point of , the one which factors through the terminal object of ; the fiber over this point is the 'non-twisted' cohomology. -
- CommentRowNumber26.
- CommentAuthorUrs
- CommentTimeMar 16th 2010
- (edited Mar 16th 2010)
Okay, right, "the fiber of the collection of
 -points of
-points of  over a given
over a given  -point of
-point of 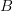 .
.But maybe then actually proper topos-language is preferable: at stage
 , twisted cohomology is the (homotopy) fiber of
, twisted cohomology is the (homotopy) fiber of 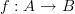 over a given element of
over a given element of 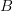 .
. -
- CommentRowNumber27.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 16th 2010
- (edited Mar 16th 2010)
fine. and we could also forget about "(homotopy)" since in the oo-topos setting there is no other meaningful fiber. so we could give the above as definition of twisted cohomology, and then unravel this to the more explicit cocycle description. -
- CommentRowNumber28.
- CommentAuthorUrs
- CommentTimeMar 16th 2010
Yes.
Right, so who is going to put this into the entry now? :-)
I have to run and catch a bus, but maybe I can do it later...
-
- CommentRowNumber29.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 16th 2010
I will make some minor edit to the entry now, where the (oo,1)-topos definition of twisted cohomology is given. later I'll copy it in my area to attemp a major clean up. -
- CommentRowNumber30.
- CommentAuthorUrs
- CommentTimeMar 16th 2010
a major clean up.
That might indeed be a good idea. Thanks!
-
- CommentRowNumber31.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 17th 2010
- (edited Mar 17th 2010)
a cleaned up version is now available here. in case you find it could be good for the nLab, just copy it in palce of the current nLab version. -
- CommentRowNumber32.
- CommentAuthorUrs
- CommentTimeMar 17th 2010
Thanks, that looks good.
One remark I would have is that the "motivating example" at the beginning is not really an immediate motivation for the definition that follows, as it requires the argument following that in turn to see how it relates. Maybe it would be better to move that alltogether into the examples section.
-
- CommentRowNumber33.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 17th 2010
I agree, twisted K-theory could be presented as the first example in the example section. this way one would also avoid the break there is now between the motivating example and G-acrions on spectra, which is presented as (and indeed is) its natural generalization. -
- CommentRowNumber34.
- CommentAuthorUrs
- CommentTimeMar 17th 2010
Yes. Please feel free to replace the nLab entry with what you have. I have no time to work on this at the moment, but I do like what you did.
-
- CommentRowNumber35.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 17th 2010
done. -
- CommentRowNumber36.
- CommentAuthorUrs
- CommentTimeMar 17th 2010
Thanks!
Now I did spent some time working more on twisted cohomology after all:
I edited the beginning, up to where the Examples-section begins:
added a sentence to the Idea-section
made the statements that follow the definition a series of formal propositions with formal proofs
polished the notation a bit here and there, for instance in changing
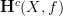 to
to ![\mathbf{H}_{[c]}(X,f) \mathbf{H}_{[c]}(X,f)](/extensions/vLaTeX/cache/latex_06f2dd8bfac4039a75af7fd11b30b356.png) (for it not to collide with the
(for it not to collide with the 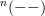 -notation).
-notation).
-
- CommentRowNumber37.
- CommentAuthorUrs
- CommentTimeMar 17th 2010
By the way, one reason (of several) why I have little right now is that I need to bring some stuff curently on my personal web into shape. Currently I am busy polishing and expanding the entry path oo-groupoid.
This has developed quite a bit, I think. I'd be interested in hearing your comments on this.
-
- CommentRowNumber38.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 17th 2010
I'll be glad to look at it. just let me know your favourite way of receiving comments: query boxes on the page? forum posts? private e-mail? other?
I've looked at your edits at twisted cohomology: it looks much better now. -
- CommentRowNumber39.
- CommentAuthorUrs
- CommentTimeMar 17th 2010
just let me know your favourite way of receiving comments: query boxes on the page? forum posts?
forum posts would be nice.
query boxes are fine, too, but I will tend to react to them quickly and then remove them. So maybe for a more coherent discussion forum posts would be better. Thanks.
-
- CommentRowNumber40.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
I was thinking back to fibration sequences and cohomology. I'll write everything for nice topological spaces, but I guess there is a natural generalization to an arbitrary (oo,1)-topos. as usual this is well known and already present on the Lab, but I find it nice to recollect it in a single post (and on my area after clean up..)
first remark is that via the homotopy hypothesis, postnikov towers become something extremely natural and simple: take a topological space , consider the oo-path groupoid , truncate this to an n-groupoid , take the topological realization of this.
similarly, whitehead towers of are obtained as fibration sequences .
since preserves fibration sequences, for any topological sapce we obtain a fibration sequence
and one recovers the well known fact that obstruction to lifting cohomology with coefficients in to cohomology with coefficients in lies in cohomology with coefficients in .
for instance, with , one recovers that obstruction to orientability is an element in , obstruction to a spin structure an element in and the obstruction to a string structure an element in .
as I said, nothing new: it was just to write an example of how the use of fibration sequences in cohomology allows to nicely rewrite very classical results -
- CommentRowNumber41.
- CommentAuthorzskoda
- CommentTimeMar 23rd 2010
I agree, twisted K-theory could be presented as the first example in the example section.
My faint memory says that the tensor product issues, hence product for classes, is more delicate in twisted K-theory than in the usual. Is this easy in this approach ?
-
- CommentRowNumber42.
- CommentAuthorUrs
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
similarly, whitehead towers
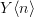 of
of 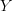 are obtained as fibration sequences
are obtained as fibration sequencesyes, very nice. I had made a remark exactly along these lines here, recently.
This needs to be polished and moved to Whitehead tower
-
- CommentRowNumber43.
- CommentAuthordomenico_fiorenza
- CommentTimeMar 24th 2010
thanks. it's nice this way we're coming to think to the same kind of constructions. I would no say "independently"; rather it seems to me a beautyful example of how the nLab discussions are creating a common point of view on the subject. I really like this.
I've seen you've cleaned up Whitehead tower and added a few related entries. I've a comment, which I'll post into the related thread -
- CommentRowNumber44.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
it seems to me a beautyful example of how the nLab discussions are creating a common point of view on the subject. I really like this.
Yes, I am very much enjoying this, too. Glad to have you around here.
-
- CommentRowNumber45.
- CommentAuthorUrs
- CommentTimeApr 21st 2010
Added an Examples-section
and a brief followup-section
meant to put the construction by Ando-Blumberg-Gepner into perspective.
-
- CommentRowNumber46.
- CommentAuthorUrs
- CommentTimeMay 3rd 2010
added to the section In terms of sections at twisted cohomology a pointer to the fully detailed proof of the statement stated there.
-
- CommentRowNumber47.
- CommentAuthorUrs
- CommentTimeAug 6th 2013
- (edited Aug 6th 2013)
Inspired by discussion with Marc Hoyois in another thread I finally went and started trying to beautify the entry twisted cohomology a little.
So far I have
given it a better and considerably expanded Idea-section
given it a better and considerably expanded Definition-section
Especially the Definition section certainly could still do with more work, but for the moment I am out of steam.
Also the Examples-section should be cleaned up and more examples should be added. Maybe later. (Or maybe Marc feels energetic to add more! :-)
-
- CommentRowNumber48.
- CommentAuthorigor
- CommentTimeFeb 21st 2014
- (edited Feb 21st 2014)
Added a section on effective computation of twisted cohomology using de Rham cohomology of the universal cover and the action of the fundamental group thereon:
The idea was inspired by the following MO answer by Peter Michor.
Would anyone know what to do if the fundamental group is not finite?
-
- CommentRowNumber49.
- CommentAuthorDavid_Corfield
- CommentTimeDec 19th 2017
I see there’s a new article in this area:
- Daniel Grady, Hisham Sati, Higher-twisted periodic smooth Deligne cohomology, (arXiv:1712.05971)
1 to 49 of 49