nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
created Mod
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeMar 19th 2010
Question: How is this different from
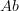 ?
? -
- CommentRowNumber3.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2010
Ab is the fibre over the ring of integers.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeMar 19th 2010
I added that remark to the entry now.
-
- CommentRowNumber5.
- CommentAuthorHarry Gindi
- CommentTimeMar 19th 2010
- (edited Mar 19th 2010)
Oh, by the way, a morphism of pairs of rings and modules (R,M) -> (S,N) the way you described is called a dihomomorphism (dihomomorphisme) on the first page of EGA I. Also, what you added made it easier to understand. Thanks!
-
- CommentRowNumber6.
- CommentAuthorTim_Porter
- CommentTimeMar 19th 2010
@Urs I think you will find that the observation of Quillen is actually referenced in Quillen's paper to Beck's thesis. It should be if it is not, as Jon Beck looked at the Abelianisation in that case. (Come to think of it it may be even earlier in Grothendieck Catégories cofibrées additives? I would have to check dates and content.)
-
- CommentRowNumber7.
- CommentAuthorUrs
- CommentTimeSep 11th 2012
- (edited Sep 11th 2012)
added to Mod in the section RMod is an abelian category more of the elementary details of the various statements there.
-
- CommentRowNumber8.
- CommentAuthorzskoda
- CommentTimeAug 31st 2022
- (edited Aug 31st 2022)
I feel that the entry Mod should be about modules/presheaves over a ringoid = small preadditive category (covariant or contravariant functors into the category of abelian groups).
Namely, all theorems written there seem at my glance to apply to this general (and still quite standard even in pre-POV literature). The only thing specific of the category Mod R for a ring R as opposed to a ringoid is that it has a finitely generated projective generator, what does not seem to be on the page.
7: abelianess as well as Ab3,4,5,6 (and duals of those) properties hold for an additive functor category if they hold for the codomain category. So it is quickest to notice that it holds for the category of abelian groups.
-
- CommentRowNumber9.
- CommentAuthorvarkor
- CommentTimeAug 31st 2022
It would make more sense to me for this page to be about the monads and (bi)modules construction (properly viewed as a virtual double category), which generalises the setting on the page currently.
-
- CommentRowNumber10.
- CommentAuthorzskoda
- CommentTimeAug 31st 2022
But this is quite a different subject with different theorems. It is about which theorems hold not about the definition.
-
- CommentRowNumber11.
- CommentAuthorUrs
- CommentTimeFeb 2nd 2023
added pointer to:
- Jarl G. Taxerås Flaten, Univalent categories of modules [arXiv:2207.03261]
(here and in related entries)
1 to 11 of 11