Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory internal-categories k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

Atrium > Mathematics, Physics & Philosophy: Day convolution and symmetric monoidal products

Bottom of Page

1 to 12 of 12

  1.  
    • CommentRowNumber1.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 20th 2010

    If we apply the day convolution to 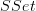SSet, we get an asymmetric monoidal product from what appears to be a symmetric monoidal product (ordinal sum) on the augmented simplex category. The strange thing is, there's nothing that appears to be asymmetric in the formula for the day convolution, so why do we end up with an asymmetric monoidal product (the join)?

    • CommentRowNumber2.
    • CommentAuthorTim_Porter
    • CommentTimeMar 20th 2010

    Is the ordinal sum symmetric? I have a feeling that there is something strange there. may be wrong ... often am!

    • CommentRowNumber3.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 20th 2010

    Yeah, I'm not sure either. Maybe someone will be able to shed some light on it.

    • CommentRowNumber4.
    • CommentAuthorTim_Porter
    • CommentTimeMar 20th 2010
    • (edited Mar 20th 2010)

    Try all the axioms of a sym. tensor product. That cannot do any harm! It may be symm. but it is worth checking.

    The point is surely similar to the order reversal on ordinals being an involution but is does not give an involution on the functor category.

    (Look at p. 13 of Phil Ehlers thesis.)

    • CommentRowNumber5.
    • CommentAuthorTim_Porter
    • CommentTimeMar 20th 2010

    I think the point is that the `obvious' isomorphism is NOT in the category $\Delta$

    • CommentRowNumber6.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 20th 2010

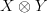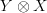    For a monoidal product to be symmetric, does it need to actually induce isomorphisms between the two objects X\otimes Y and Y\otimes X, or does there just need to exist one?

    • CommentRowNumber7.
    • CommentAuthorTim_Porter
    • CommentTimeMar 20th 2010

    The two 'bifunctors' have to be naturally isomorphic at least. It is not clear what`induce isomorphisms' might mean.

    • CommentRowNumber8.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 20th 2010
    • (edited Mar 20th 2010)

    Oh, I see! They're braided (but not symmetric).

    • CommentRowNumber9.
    • CommentAuthorTim_Porter
    • CommentTimeMar 20th 2010

    I think it is worse than that. There is no natural isomorphism between the two sides.

    • CommentRowNumber10.
    • CommentAuthorHarry Gindi
    • CommentTimeMar 20th 2010
    • (edited Mar 20th 2010)

    What's an example of a symmetric monoidal product then? I can't think of one offhand. Maybe the tensor product? If not, the symmetric product? (of modules, of course).

    • CommentRowNumber11.
    • CommentAuthorTim_Porter
    • CommentTimeMar 21st 2010

    Those are examples but why be that complicated. Cartesian product will do.

    • CommentRowNumber12.
    • CommentAuthorUrs
    • CommentTimeMar 21st 2010

    The equivalent definition stated at join of quasi-categories

    S \diamondsuit T := colim( S \to S \times T \times \Delta[1] \leftarrow T )

    exhibits the directed structure of the join more manifestly: it's all in the orientation of \Delta[1] = (0 \to 1).

1 to 12 of 12

  1.