nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
I have to admit that I simply cannot parse many of the entries on type theory and related.
Now, this is certainly my fault, as I am not spending any considerable time to follow this. But on the other hand my impression is that many statements here are not overly complicated, and that I ought to be following at least roughly what's going on. But I don't.
One thing is that when I try to look up precise definitions such as at type theory I run into long pieces of text. I am not sure what to make of this.
My understanding was at some point that all of type theory is really just another way of speaking about categories. Instead of "object"
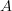 we say "type"
we say "type"  . Instead of morphism
. Instead of morphism 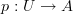 we say
we say 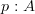 "
"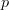 is of type
is of type  " and the like.
" and the like.Can we have some Rosetta-stone entry where all the type-theoretic language is translated into plain category theory this way?
For instance I am suspecting that what is going on at identity type is somehow another way of saying equalizer. But I am not sure. Can anyone help me?
-
- CommentRowNumber2.
- CommentAuthorHarry Gindi
- CommentTimeMar 22nd 2010
I agree with your assessment.
-
- CommentRowNumber3.
- CommentAuthorzskoda
- CommentTimeMar 22nd 2010
identity type weak factorization system is required in few entries at least one of which makes the impression that the writer thought the entry exists in nlab. Maybe it does under another name or as a paragraph in some existing entry ?
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
- (edited Mar 22nd 2010)
Here is one concrete question that I have:
at display map it says that a morphism
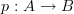 in a category may be understood as a dependent type.
in a category may be understood as a dependent type.This is understand: I understand that by "type" we really just mean "object of a category" (right??). So a morphism
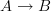 is one object parameterized over another object (a bundle of objects) and hence is a "dependent type".
is one object parameterized over another object (a bundle of objects) and hence is a "dependent type".But then further below it says that in type theory speak we write for
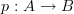 instead
instead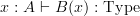
My first question is: how does one read this out in English?
My second question is: what is the piece ": Type" here good for?
And my third question is: where did the
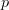 disappear to?
disappear to? -
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeMar 22nd 2010
I added two query boxes with elementary questions to the beginning of type theory.
But I'll stop now with asking questions, until Mike or Toby have had a chance to reply a bit.
-
- CommentRowNumber6.
- CommentAuthorMike Shulman
- CommentTimeMar 23rd 2010
Thanks for bringing this up, I want to make this comprehensible. Let me try to answer your questions.
Of course, in type theory proper, "type" does not just mean "object of a category," but if all one cares about is categorical semantics, then it's okay to think about it in that way. But I think it's misleading to similarly identify variables with morphisms. A variable
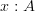 in type theory should be considered as a "formal element of the type
in type theory should be considered as a "formal element of the type  ." You can probably think of it as a generalized element, but this could be misleading, since its domain is not fixed. Think back to basic calculus when we write
." You can probably think of it as a generalized element, but this could be misleading, since its domain is not fixed. Think back to basic calculus when we write 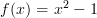 . What is
. What is  ? It's not a particular real number, or even a "generalized real number" -- it's a variable which serves to define the function
? It's not a particular real number, or even a "generalized real number" -- it's a variable which serves to define the function 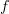 , and for which any particular real number could be substituted in order to evaluate
, and for which any particular real number could be substituted in order to evaluate 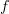 at that real number.
at that real number.Thus when we write
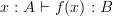 in type theory, we mean "for any element
in type theory, we mean "for any element  of
of  , there is a corresponding specified element
, there is a corresponding specified element 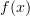 of
of 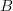 ," i.e.
," i.e. 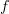 is a "function" from
is a "function" from  to
to 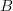 . The categorical semantics interprets such a function as a morphism from A to B in the category in question. It doesn't interpret the variable
. The categorical semantics interprets such a function as a morphism from A to B in the category in question. It doesn't interpret the variable  by anything at all;
by anything at all;  is an artifact of the type theory which is invisible to the category theory. (The category theory would maybe be like referring to the function
is an artifact of the type theory which is invisible to the category theory. (The category theory would maybe be like referring to the function 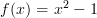 above as "that function which squares its argument and then subtracts one from it.)
above as "that function which squares its argument and then subtracts one from it.)@Zoran: No, identity type weak factorization system does not exist yet, afaik. My understanding is that it's common wiki-practice to add links to pages that don't exist yet, so that the links will work as soon as the page is created. (-:
-
- CommentRowNumber7.
- CommentAuthorMike Shulman
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
Going on to your questions about dependent types, one pedantic way to read
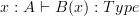 is as "in the context of any variable
is as "in the context of any variable  of type
of type  , there is a type
, there is a type 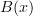 ." A type theorist would probably just say "
." A type theorist would probably just say "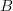 is a type dependent on
is a type dependent on  ." There is a formal analogy to a sequent of the form
." There is a formal analogy to a sequent of the form 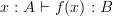 , read as "in the context of any variable
, read as "in the context of any variable  of type
of type  , there is a term
, there is a term 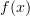 of type
of type 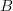 ." And you can make that precise -- in some type theories, types themselves are just terms of type
." And you can make that precise -- in some type theories, types themselves are just terms of type 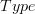 . So that I think answers your second question: the role of the
. So that I think answers your second question: the role of the 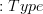 is that it's what's being asserted, namely, than
is that it's what's being asserted, namely, than 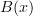 is a type. If we left off the
is a type. If we left off the 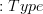 then we wouldn't have an assertion, since
then we wouldn't have an assertion, since 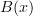 is a type, not an assertion.
is a type, not an assertion.Finally, the
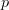 has disappeared into the
has disappeared into the 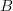 , in the same way that the multiplication and identity of a group disappear into the group when we say "consider a group
, in the same way that the multiplication and identity of a group disappear into the group when we say "consider a group 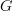 " instead of "consider a group
" instead of "consider a group 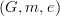 ." Similarly, it's fairly common to speak of objects in a slice category
." Similarly, it's fairly common to speak of objects in a slice category 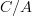 without giving an explicit name to the projection map unless necessary.
without giving an explicit name to the projection map unless necessary. -
- CommentRowNumber8.
- CommentAuthorMike Shulman
- CommentTimeMar 23rd 2010
And yes, at least in extensional type theory, identity types are a type-theoretic incarnation of equalizers (or, more precisely, of diagonals, which then can be pulled back to give equalizers). But in intensional type theory, and higher-categorical type theory, they are more subtle, as mentioned (too briefly) in the article.
-
- CommentRowNumber9.
- CommentAuthorHarry Gindi
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
I think that adding in a note about abuses of notation to nLab pages would be most helpful, especially in pages on something more esoteric like type theory. I also think that noting abuses of notation is part of being pedagogically conscientious.
-
- CommentRowNumber10.
- CommentAuthorTobyBartels
- CommentTimeMar 23rd 2010
I have tried to answer your query boxes at type theory, Urs.
-
- CommentRowNumber11.
- CommentAuthorMike Shulman
- CommentTimeMar 23rd 2010
@Harry: yes, by all means let's explain the notation as much as possible. I wrote what I wrote from my idosyncratic viewpoint in a way that made sense to me, so now let's discuss how to make it the most comprehensible to everyone. I do object to calling such uses of notation "abuses" since it gives the impression there is something wrong with them, but certainly whatever notation is a stumbling block for people should be explained.
-
- CommentRowNumber12.
- CommentAuthorHarry Gindi
- CommentTimeMar 23rd 2010
"Abuse of notation" is a standard term. It was not meant as a slight! =)
-
- CommentRowNumber13.
- CommentAuthorMike Shulman
- CommentTimeMar 23rd 2010
Yes, I know it's standard, but I still object to it. (-:
Actually, after thinking about it some more, I think that the "abuse" really flows the other way. That is, the dependent type
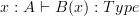 should be regarded as containing all the information of an object of the slice category
should be regarded as containing all the information of an object of the slice category 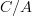 , namely a morphism together with its domain. The abuse is in referring to the domain alone by the same letter used for the dependent type; really we should notate the morphism as something like
, namely a morphism together with its domain. The abuse is in referring to the domain alone by the same letter used for the dependent type; really we should notate the morphism as something like 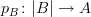 .
.And in fact, both the domain and the morphism already have names within the type theory. The domain, considered as an object of the category in its own right, is the dependent sum type
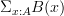 , and the morphism from this to
, and the morphism from this to  is the projection
is the projection 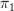 onto the indexing type of the dependent sum.
onto the indexing type of the dependent sum. -
- CommentRowNumber14.
- CommentAuthorTobyBartels
- CommentTimeMar 23rd 2010
Although not all type theories have dependent sums. And then this simplification, in which we identify objects of the category with types, breaks down; we really have to identify objects with contexts.
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeMar 23rd 2010
Thanks Mike, thanks Toby!
That helps. I have turned the query boxes at Categorical semantics into genuine text, using replies here and Toby's replies there. Please check if this is correct now.
-
- CommentRowNumber16.
- CommentAuthorzskoda
- CommentTimeMar 23rd 2010
I do object to calling such uses of notation "abuses" since it gives the impression there is something wrong with them
The wrong thing is that it spoils theoretical uniquness of the notation by using shortcuts which are overloaded and hence can be misinterpreted if a computer would analyse it automatically. Anybody who was programming artificial intelligence knows the pains of the abuse of notation. I find the expression cute and the very fact that it is standard and accepted implies that the abuse is OK from practical mathematical point of view as long as the people communicating mathematics do feel so. The fact that it is labelled as nongenuine can, in the cases of misunderstanding, give the right to the listener to call the speaker to go back to the true underlying formal or more formal expression.
-
- CommentRowNumber17.
- CommentAuthorHarry Gindi
- CommentTimeMar 23rd 2010
- (edited Mar 23rd 2010)
The Wikipedia page actually gives a pretty good idea of how it's generally meant in the mathematical community.
In written work as well, noting abuses of notation when they're first introduced can save a lot of time and pain for the reader. That's why when you introduce a definition, you should give it a formal definition and then note that there is an abuse of notation going on. This way, if the reader looks up the definition in the index, he/she will also be able to find the conventions! (For example, I was reading Michael Spivak's book on Differential geometry, and I could not figure out for the life of me what
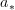 meant. Needless to say, it was due to an abuse of notation. (It's not actually a pushforward at all)).
meant. Needless to say, it was due to an abuse of notation. (It's not actually a pushforward at all)). -
- CommentRowNumber18.
- CommentAuthorMike Shulman
- CommentTimeMar 24th 2010
@Zoran: But overloaded operators and polymorphism are ubiquitous in computer science, and powerful type inference procedures exist to resolve ambiguity. I'm not saying that such simplified notations aren't harder for a computer to parse (and occasionally may require additional annotation from the user), but I don't think that makes them "wrong" or "not true."
@Harry: I completely agree that notation should be introduced, and indexed.
-
- CommentRowNumber19.
- CommentAuthorMike Shulman
- CommentTimeMar 24th 2010
@Toby, good point. It is true, though, that you only need dependent sums if you also have dependent types -- otherwise, finite product types suffice. Of course in both cases there is then also the question of equalizers and more general subobjects, and at some point we have to figure out exactly what was meant by the words "correspond to" in the phrase "types correspond to objects." But I think in the overview, the "(with various subtleties)" is probably sufficient where currently placed.
@Urs, thanks! I like how it is now.
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
- (edited Mar 24th 2010)
@Urs, thanks! I like how it is now.
Okay, good. I like the notation, now that I fully understand how it is meant to be read. I feel like it should have been obvious to me without asking.
In fact, this categorical semantics notation and language already appears in structural set theory, as in Todd's discussion ot ETCS, of course. It is really the language that says that each morphism in a category is a natural map of sets of generalized elements. So it's really the language that describes all the ingredients of a category
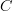 after their Yoneda embedding into
after their Yoneda embedding into 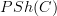 .
.Just for the sake of it, I added a sentence to this extent to type theory:
So the notation
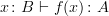 is a direct reflection of the description of the morphism
is a direct reflection of the description of the morphism 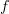 under the Yoneda embedding
under the Yoneda embedding 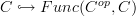 . Since the Yoneda embedding is a full and faithful functor, this is indeed an entirely equivalent characterization of the morphism
. Since the Yoneda embedding is a full and faithful functor, this is indeed an entirely equivalent characterization of the morphism 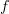 .
. -
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
I further edited type theory:
I went to the paragraph that talks about dependent types and in an analogous manner as before tried to unwind everything into the underlying categorical language.
Please have a look!
-
- CommentRowNumber22.
- CommentAuthorHarry Gindi
- CommentTimeMar 24th 2010
@Urs: Mike has said before that SEAR is just type theory in a disguise.
So.. How about the theory of unramified types....
-
- CommentRowNumber23.
- CommentAuthorMike Shulman
- CommentTimeMar 24th 2010
@Urs: looks good, I did a bit more editing.
-
- CommentRowNumber24.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
- (edited Mar 24th 2010)
Okay.
I couldn't stop myself and edited a bit more, still:
where dependent types are being introduced I expanded a bit more and mentioned the new notation
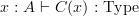
then I added some subsection titles, since this part is becoming fairly long now. What do you think how the new toc looks? I like it better this way.
-
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
- (edited Mar 24th 2010)
Armed with my improved understanding, I am now looking at identity type again.
I still don't follows this, though.
-
- CommentRowNumber26.
- CommentAuthorzskoda
- CommentTimeMar 24th 2010
- (edited Mar 24th 2010)
and powerful type inference procedures exist to resolve ambiguity
But those must be probabilistic in general (Edit: in cases which go beyond comparativley simple overloading in programming languages). These algorithms are for more special and simple situations than in human mathematical comunication in which we are on daily basis witnesses in seminars where the informal shortcuts confuse listeners. This is an economy which does lead to occasional errors, hence there is a feature which is not perfect. That does not say that imperfect objects are not often useful, but they are imperfect and stepping down from more unambiguous to more ambigous notation is hence a kind of abuse. Even higher level of ambiguity is in the natural language discourse, and the level of disambiguation of deixis has not been radically raised in last 30 years, as it would require so much of the context and real artificial intelligence that mere algorithm improvement and speed does not help that much. I have some sizeable hands on experience on both the computational linguistics and the compiler construction.
-
- CommentRowNumber27.
- CommentAuthorMike Shulman
- CommentTimeMar 25th 2010
Urs, the subsections look good. You're right that
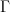 is a context; I think
is a context; I think 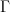 is pretty universally used to denote an arbitrary context, so sometimes I may forget to mention what it means.
is pretty universally used to denote an arbitrary context, so sometimes I may forget to mention what it means.The "big rule" is defining a term constructor called J. I tried to explain this in the paragraph which follows: J(...) is a new term, with some specified type, which the identity type rule allows us to form.
Finally, if I understand you correctly, the first half of the lower line copies the first part of the upper line because they are two different assertions in the same context. The first hypothesis asserts that in some context we have a type
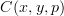 , while the conclusion asserts that in that same context we have a term belonging to the type
, while the conclusion asserts that in that same context we have a term belonging to the type 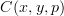 , namely
, namely 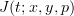 .
. -
- CommentRowNumber28.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
This seems just as complicated as material set theory.
(I was going to delete my comment, but mike answered it, so I've put it back the best I could.)
-
- CommentRowNumber29.
- CommentAuthorMike Shulman
- CommentTimeMar 25th 2010
Zoran, I'm not disagreeing with any of that, I just don't think the word "abuse" is appropriate. In fact, I think that often things labeled "abuses" of notation are actually not ambiguous at all. For instance, if
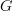 is a group, we always write
is a group, we always write 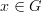 to mean that
to mean that  is an element of the underlying set of
is an element of the underlying set of 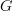 . People call this an abuse of notation, but since
. People call this an abuse of notation, but since 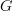 only has one underlying set, there is really nothing ambiguous about it. (Unless one insists that a group is really a Kuratowski ordered triple, in which case
only has one underlying set, there is really nothing ambiguous about it. (Unless one insists that a group is really a Kuratowski ordered triple, in which case 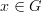 might have a totally different meaning, but that's just silly.)
might have a totally different meaning, but that's just silly.) -
- CommentRowNumber30.
- CommentAuthorMike Shulman
- CommentTimeMar 25th 2010
Harry, my problem with material set theory is not that it's complicated (it's not, really, in its own right) but that the process of coding mathematics into it is unnatural, introduces superfluous data, enables meaningless questions, and discards important typing information. Also, structural set theory and type theory have a much more natural categorical semantics, while type theory also has important connections to computability and automated proof. I freely admit that type theory is more complicated than set theory (at a basic level, anyway); its advantages lie elsewhere.
-
- CommentRowNumber31.
- CommentAuthorHarry Gindi
- CommentTimeMar 25th 2010
I think that we should build structural set theory on top of material set theory. This is extremely easy to do and feels more natural in a sense. For instance, a lot of the complicated definitions from type theory can be stated more easily using a material set theory.
Think of it this way: material set theory is like machine code or binary, while type theory gives us a higher-level language to deal with things.
-
- CommentRowNumber32.
- CommentAuthorDavidRoberts
- CommentTimeMar 25th 2010
The whole point of foundations is not to build on top of another foundation. Sure you can build a model of ETCS or SEAR from ZFC, but that is not necessary what you want to do. The point is to extract the necessary structure (i.e. the category) and throw away
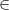 , which allows the construction of stupid questions (like is
, which allows the construction of stupid questions (like is 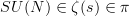 ?).
?). -
- CommentRowNumber33.
- CommentAuthorMike Shulman
- CommentTimeMar 25th 2010
- (edited Mar 25th 2010)
Actually, I think type theory is more like machine code, since it's more directly connected to first-order logic. Material set theory is just a particular first-order theory that lives inside a type theory. (-:
And why on earth would you believe that material set theory is like machine code? That would mean that somehow the integer 2 "really is" the von Neumann ordinal
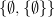 (or maybe a different set), but the type theory doesn't know it. It's much more reasonable to say that 2 is an element of the type of natural numbers, which in turn can be modeled in material set theory by the set of finite von neumann ordinals, but also in lots of other ways.
(or maybe a different set), but the type theory doesn't know it. It's much more reasonable to say that 2 is an element of the type of natural numbers, which in turn can be modeled in material set theory by the set of finite von neumann ordinals, but also in lots of other ways. -
- CommentRowNumber34.
- CommentAuthorMike Shulman
- CommentTimeMar 25th 2010
Back on the original subject, I added some more explicit explanation to context about morphisms of contexts in terms of type theory. I'm not sure I put it in the right place, though.
-
- CommentRowNumber35.
- CommentAuthorUrs
- CommentTimeMar 25th 2010
Thanks again, Mike.
I tried to explain this in the paragraph which follows:
Right, I should spend more time looking into this. The trouble is that I am really doing something else and just following the type theory development with half an eye.
I want to get to the point where I can clearly understand the relation to
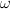 -groupoids. I certainly get the basic idea that an identity type is like an
-groupoids. I certainly get the basic idea that an identity type is like an 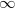 -groupoid of paths or of equivalences between two objects. But eventually I want to understand this on a more formal level, for myself.
-groupoid of paths or of equivalences between two objects. But eventually I want to understand this on a more formal level, for myself.But not right now. I need to take care of some Cartesian fibrations now...
1 to 35 of 35
 a
a 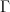 ". Hope this is right.
". Hope this is right.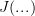 ?
?