nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorUrs
- CommentTimeMar 24th 2010
renamed model structure on marked simplicial oversets to model structure for Cartesian fibrations
merged the material that was at marked simplicial set (now marked simplicial set > history) into this entry
expanded the entry a bit, but still working on it...
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeMar 26th 2010
further expanded the list of central propositions at model structure for Cartesian fibrations
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
I expanded on the discussion of how marked simplicial sets are cartesian closed. This is now a new section called "Cartesian closure".
In particular I write out what I think is a detailed proof how the Cartesian closure works. The strategy chosen is to use presheaves on a category
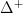 that is like the simplex category, but with one more object
that is like the simplex category, but with one more object ![[1^+] [1^+]](/extensions/vLaTeX/cache/latex_6c6590501c4012caf0ffcafbaee358ca.png) added, that will parameterize the marked edges. Then there is the standard cartesian closed structure on presheaves on
added, that will parameterize the marked edges. Then there is the standard cartesian closed structure on presheaves on 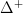 and one checks that this restricts to one on the full subcategory which is marked simplicial sets.
and one checks that this restricts to one on the full subcategory which is marked simplicial sets.Possibly overkill, but I struggled a bit to find a really clean argument.
-
- CommentRowNumber4.
- CommentAuthorUrs
- CommentTimeApr 7th 2010
expanded the section on Marked anodyne morphisms
-
- CommentRowNumber5.
- CommentAuthorTim Campion
- CommentTimeFeb 28th 2020
Lurie only claims that the covariant / contravariant model structures are left proper. In fact, they are not right proper, even over a point: the usual counterexample to right properness of the Joyal model structure works here too. Namely, the inclusion of the 1-face into the 2-simplex is an isofibration of nerves of gaunt categories, and hence a fibration in the model structure on . The inclusion of the 1-horn into the 2-simplex is a weak equivalence. But the pullback of the latter along the former is not a weak equivalence.
-
- CommentRowNumber6.
- CommentAuthorHurkyl
- CommentTimeJan 14th 2021
1 to 6 of 6