Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory object of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes

Show all

15001 to 15060 of 15187

  1. <
  2. 1
  3. ...
  4. 247
  5. 248
  6. 249
  7. 250
  8. 251
  9. 252
  10. 253
  11. 254
  12. >

    • no, I didn't create an entry with that title.

      but I added to n-fibration a brief link, though, to the concept that is currently described at Cartesian fibration, which models Grothendieck fibrations of (oo,1)-categories.

      This here is mainly to remind me that there is need to polish and reorganize the nLab entries on higher fibrations into something more coherent.

    • I fixed a bunch of broken links on the lab just now. In case anybody is wondering what all of those edits were.

    • I have just made links to all of the contentful orphaned paged on the main nLab web. However, they may still be walled gardens; Instiki doesn't find those automatically.

      In general, when you create a new page, it's a good idea to create a link to it from some existing page on a more general topic. (The links that I just made may not have been the best!) That way, it's more likely that people will actually find their way to your new page.

    • I wanted to start expanding on the big story at nonabelian Lie algebra cohomology, but then found myself wanting to polish first a bit further the background material.

      I came to think that it is about time to collect our stuff on "oo-Lie theory".

      So I created a floating table of contents

      and added it to most of the relevant entries.

      This toc is based on the one on my personal web here -- but much larger now -- and still contains some links to my web, where I am trying to develop the full story. If anyone feels ill-at-ease with these links to my personal web, let me know.

    • It looked to me like Urs hit Ctrl-V instead of Ctrl-C there, so I rolled back, but now Urs is editing again, so probably he's just doing something that I interrupted. Since I can't leave a note there now, I'll leave one here: I won't interfere again, Urs.

    • added to (infinity,1)-operad the definition/proposition of the model structure for the category of (oo,1)-categories of operations here

    • I added to vertical categorification the comments that I'd made at MathOverflow, as Urs has requested. I'm not sure that I'm happy with where I put them and how I labelled them, but maybe it's better if other people judge that.

    • Added some more to the ongoing discussion about composition at evil.

      (fixed)
    • I'd like to add the following "shape" to http://ncatlab.org/nlab/show/limit#types_of_shapes_of_limit_cones_17 :

      The limit of the identity functor Id: C --> C is the initial object of C (it it exists).
    • I've added the latest, almost complete, draft of my thesis to my personal web - go via David Roberts. Comments on introduction are welcome, if you feel so inclined. Just put them on David Roberts.

      On a related note, is it quite legitimate to post updates on personal webs here? (Now that I've already done it)

      David Roberts
    • Edited the page category theory. Mostly about that certain presheaves are the same as categories and the long discussion at the end with an idea how to solve my problem about CW-complexes. Removed precursors link since there is nothing about them in nLab. This new logging is a bit confusing and harder to read.

      -Rafael

    • Created universal algebra in a monoidal category

      In the lab book metaphor, this page is some jottings of stuff that I'm pretty sure must be out there (as it's a fairly obvious thing to do) but have no idea of what it's called (hedgehogs, perhaps?). So I'd be grateful if someone strong in the ways of Lawvere theories could stop by and help me out.

      (Plus I had to make up the notation and terminology as I went along so that's all horrible)

      Hopefully the big box at the top of the page makes this clear!

    • I apologize in case this discussion is already open and I have been unable to find it.

      There is something I am unable to undrstand in the definition of extended TQFT as on the nLab page http://ncatlab.org/nlab/show/extended+topological+quantum+field+theory

      Namely, it seems to me that the recursive definition should rather end with "smooth compact oriented (n-m+1)-manifolds to R-linear (m?2)-categories"

    • One of these has started (or continued) a conversation at the bottom of graph.

    • I'm guessing that ferrim is spam. If no-one says anything to the contrary within 24hrs then I'll add it to the spam category.

      If it is spam, it's either a random spambot post or it's someone testing to see how vigilant we are. If the latter, as there's no content then they may simply test to see if the link stays active. In which case, our previous "policy" of blanking the content won't send the right signal here (especially as there's no content to blank). Is there any objection to renaming spam entries? Say, as 'spam (original title)' (or whatever the allowable punctuation characters are)?

    • In entry groupoid object in an (infinity,1)-category there is a passage

      "it is the generalization of Stasheff H-space from Top to more general ?-stack (?,1)-topoi: an object that comes equipped with an associative and invertible monoid structure, up to coherent homotopy"

      I repeat what I documented in earlier discussion on H-space: H-spaces are widely used terminology since 1950, thus before Stasheff work which of course is an important work on coherencies for them. So it is likely improper to say Stasheff H-space...Stasheff has REFINEMENTS of H-spaces, namely $A_n$-spaces and the group-like case is A infty spaces.

    • Somebody named ‘Harry’ has a comment at evil. Presumably it is of interest to Mike and me.

    • I see Mike's 1-category equipment

      May I vote for the following: we should "play Bourbaki" and correct the naming mistake made here. The obvious name one should use is "pro-morphism structure".

      We equip a category with pro-morphisms.

      We equip a category with a pro-morphism structure.

      Or, if you insist,

      We equip a category with pro-arrows.

      We equip a category with a pro-arrow structure.

      But the day will come when you want a pro-2-morphism structure. And then one will regret having used "arrow" instead of "morphism".

      I mean, compared to issues like "presentable" versus "locally presentable", this idea of saying just "equipment" is a bit drastic, to my mind.

    • I'd like to write something about a Quillen equivalence, if any, between model structures on

      • n-connected pointed spaces

      • grouplike E-n spaces .

      With the equivalence given by forming n-fold look spaces.

      But I need more input. I found a nice discussion of a model structure on n-connected pointed spaces in A closed model category on (n-1)-connected spaces. I suppose there is a standard model structure on E-k algebras in Top. Is a Quilen equivalence described anywhere?

    • I added to directed colimit the \kappa -directed version, for some regular cardinal \kappa .

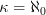      We should maybe also add to directed set the \kappa -directed version. What we currently descrribe there is just the \kappa = \aleph_0 -directed version.

      Accordingly then I also added to compact object the definition of the variant of \kappa -compact objects.

      At small object previously it mentioned " \kappa-filtered colimits". I now made that read " \kappa-directed colimits".

      I hope that's right. If not, do we need to beware of the differene?

      • created entry for Dan Freed and added some links to articles by him here and there

      • expanded the discussion of face maps at dendroidal set a little

    • I did a wee bit of editing of "Dold-Kan correspondence", trying to incorporate Kathryn Hess' wisdom into this page. A lot of this stuff involves the monoidal aspects of the Dold-Kan correspondence, but I was too lazy to edit the separate page "monoidal Dold-Kan correspondence". I would ideally like that page to focus equal attention to chain complexes as it now does to cochain complexes!

    • I put a question at CommCoalg for those knowledgeable about accessible categories: is this category locally presentable?

    • Added some discussion to skeletal category about how skeletality doesn't imply uniqueness-on-the-nose for categorical constructions, tempting though it may be to suppose that.

    • Somewhat stubby beginning, but with a link to an old paper of Barr which may turn out to be useful for universal algebra in a monoidal category. Some discussion of measuring coalgebras is generalized to the framework of PROPs.

    • I've started work at the zen garden (doriath). Stage one is to add customisable tags to all the pieces that we can reasonably adjust in the CSS. At the moment, these are all in red to make it easy to see them and to see if I've done it right - I ran it through a script to add tags to everything and I know that it got confused once or twice so there's a bit of manual work to do. Once I'm happy with that, I'll put up a sample along the lines of what Toby was thinking: having the CSS declarations in separate pages that can be "swapped in" with a minimum effort. Then people can copy that and see what the Zen Garden looks like with their changes. I'll try to make the sample so that it's really easy to change things so that those without and CSS knowledge can still have a go.

    • Etymology and pronunciation at ionad

    • wrote a fairly long Idea section at cohomology

      since the question keeps coming up and I noticed that the entry did a rather suboptimal job of describing the nice observation to be described here.

    • Added another characterisation of the full image as a pullback in Cat.

      David Roberts

    • added to negative thinking an explicit list of related entries and the floating higher cat theory toc

      I think this is important enough to show the reader as much of the grand picture as possible

    • I figured that we could stand to have an article on TAC, so I started one.

    • I thought I'd add something about the Gelfand-Neumark theorem

      The category of commutative von Neumann algebras is contravariantly equivalent to the category of localizable measurable spaces.

      to measurable space, but see we don't have anything on localizability.

      I also mentioned the theorem at von Neumann algebra. But what should one then say that a general von Neumann algebra is a noncommutative localizable measurable space? Normally one says noncommutative measure space.

    • I may have overlapped an edit with you at initial algebra. ( It's no longer locked, but you didn't change it again, so maybe it timed out.)

    • Over on MO Denis-Charles Cisinki kindly replied to some issues that I am recently working on here. See this.

    • It's not technically part of the main nLab (yet), but I asked a question at

      Cograph (ericforgy)

    • Couple of points (pun not intended) at ionad. Also remark about categorified subobject classifiers

      David Roberts

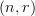    • I rearranged higher category theory - contents. It seemed wrong to have everything as a special case of n-categories/(n,r)-categories except for \infty-categories/\omega-categories. But it seemed right to list the latter up front, as the all-subsuming concept. So I basically reversed the order. (I also added a few entries.)

15001 to 15060 of 15187

  1. <
  2. 1
  3. ...
  4. 247
  5. 248
  6. 249
  7. 250
  8. 251
  9. 252
  10. 253
  11. 254
  12. >
Top of Page