Not signed in (Sign In)

Not signed in

Want to take part in these discussions? Sign in if you have an account, or apply for one below

  • Sign in using OpenID

Site Tag Cloud

2-category 2-category-theory abelian-categories adjoint algebra algebraic algebraic-geometry algebraic-topology analysis analytic-geometry arithmetic arithmetic-geometry book bundles calculus categorical categories category category-theory chern-weil-theory cohesion cohesive-homotopy-type-theory cohomology colimits combinatorics complex complex-geometry computable-mathematics computer-science constructive cosmology definitions deformation-theory descent diagrams differential differential-cohomology differential-equations differential-geometry digraphs duality elliptic-cohomology enriched fibration foundation foundations functional-analysis functor gauge-theory gebra geometric-quantization geometry graph graphs gravity grothendieck group group-theory harmonic-analysis higher higher-algebra higher-category-theory higher-differential-geometry higher-geometry higher-lie-theory higher-topos-theory homological homological-algebra homotopy homotopy-theory homotopy-type-theory index-theory integration integration-theory k-theory lie-theory limits linear linear-algebra locale localization logic mathematics measure-theory modal modal-logic model model-category-theory monad monads monoidal monoidal-category-theory morphism motives motivic-cohomology nlab noncommutative noncommutative-geometry number-theory object of operads operator operator-algebra order-theory pages pasting philosophy physics pro-object probability probability-theory quantization quantum quantum-field quantum-field-theory quantum-mechanics quantum-physics quantum-theory question representation representation-theory riemannian-geometry scheme schemes set set-theory sheaf simplicial space spin-geometry stable-homotopy-theory stack string string-theory superalgebra supergeometry svg symplectic-geometry synthetic-differential-geometry terminology theory topology topos topos-theory tqft type type-theory universal variational-calculus

Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.

Welcome to nForum
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).

nLab > Latest Changes

Show all

15061 to 15120 of 15187

  1. <
  2. 1
  3. ...
  4. 246
  5. 247
  6. 248
  7. 249
  8. 250
  9. 251
  10. 252
  11. 253
  12. 254
  13. >
    • Added to initial algebra the proof of Lambek's theorem, that the algebra structure of an initial algebra is an isomorphism. Also added to natural numbers object Freyd's finite colimit characterization in a topos, with a partial proof of same.

    • Created diagrammatic order. I attempted to strike a neutral tone in describing the dispute, but if you think I failed, please help.

    • I've notices that the links at Klein 2-geometry to the earlier parts are broken (something to do with the pages at Geocities). I recall hearing that someone made some more permanent copies. Is this true and if so, where are they?

      I said some embarrassingly naive things there, but one must preserve what progress was made.

      -David Roberts

    • created cochains on simplicial sets

      I reference there a very useful but unpublished note by Peter May that he sent me by email after he got over his astonishment that I didn't know that the Eilenberg-Zilber E_oo operad acts on cochains on a simplicial set.

      It would be great if I were allowed to upload this note to the nLab and link it at that entry. I'll see if I ask by email, but maybe Mike can mention it over lunch? I feel like Peter May feels already pestered enough by my ignorance.

    • I expanded categorification a little.

      I had intended to point to it from a MathOverflow question, but now I feel the entry is still too underdeveloped. Hopefully we'll eventually find the time and energy to enter the big examples that drive the interest in categorification.

    • I started a page on braided monoidal 2-category. Not that I have anything interesting to say on the subject, but I would like to know how to get them as module 2-categories over a monoidal category.

    • created thin homotopy to service bicategory, at which I added the necessary qualifier 'Hausdorff' to the existence of the quotient of Pi_2 by thin homotopies. There is only a passing mention of the smooth version as I only needed the topological case.

      -David Roberts

    • At cartesian morphism a query/request for an anafunctor treatment of what is essentially the pseudofunctor associated to a fibration

      David Roberts
    • Our cogroup entry is described here as 'meager'. Can we expand it?
    • created Christoffel symbol for the MathOverflow discussion at http://mathoverflow.net/questions/3847/what-is-the-geometric-significance-of-cartans-structure-equations

    • I started ordered pair to discuss how one might define such a thing in various foundations of mathematics.

    • I added a section to Gram-Schmidt process on "categorified Gram-Schmidt" (which would apply to 2-Hilbert spaces). This is illustrated with some representation-theoretic calculations which James Dolan showed me years ago; even though the write-up is still in a raw state, the calculations are way cool and should not be lost to posterity.

    • I have just posed the question:

       If we want to weaken this even further to provide a 
 simplicial model of, for example, a ((?,2)-category?, 
 how would we do this?

 Would we apply the lifting condition on all but three of 
 the indicies… and if so which three? (The first, last and ????)

      at quasi-category.

      Any and all thoughts would be appreciated.

    • I created a page for Riemannian metric based on a "blog post": http://deltaepsilons.wordpress.com/2009/10/27/riemannian-metrics-and-connections/ and a suggestion of Urs Schreiber.

    • I added an "idea" to loop space . Not claiming, though, that everybody will find this idea the most helpful one. But to some extent I think it is.

      I had another look at delooping

      Eric, you drew some nice-looking diagrams there in the discussion section. At some point in the discussion I say that I don't understand these diagram. I still don't! :-)

      It would be nice if we could converge on this, because then we could move the diagrams out of the discussion into the text as a useful illustration.

      Could you describe in words what you mean these diagrams are depicting? I am guessing that probably we are just thinking of what an arrow and a point means in such a diagram differently. Let's sort this out. If we agree that the diagrams make sense they should feature more prominently, if we come to the conclusion that there is some misunderstanding we should put a clearer warning to the reader.

    • I added a section to idempotent monad on the idempotent monad associated with a monad.

    • I have been polishing the entry Chevalley-Eilenberg algebra on my personal web a bit.

      I thought it would be good to announce here what it is that I am currently thinking about. If nothing else, this will explain which entries you all see me working on here and thereby maybe facilitate interaction more.

      So currently I am thinking about the sought-for proposition that is now stated in the section Properties at the above entry. It sure looks like something like this proposition ought to be right, but I am not there yet.

    • I was kindly being alerted that the following long-awaited references are now available:

      Paul Goerss's account of the Hopkins-Miller-Lurie theorem, now linked to at A Survey of Elliptic Cohomology

      Lurie part VI on little cubes oo-operads, now linked to from Jacob Lurie

    • Rather than ask whether it's worth it and have Urs say "do it, don't talk about it!", I started a page to compare different notions of completion. Fortunately, we are well supplied with experts on the subject. What would be great would be a comparison of different completion processes. How widely they are applicable, e.g., to the enriched case? In which situations two or more coincide, etc.
    • A question at strict epimorphism for Mike Shulman. Or anyone else who has thought about bicategorical notions of epimorphisms.

      -David Roberts

    • Started a list at n-category of all the existing definitions of higher categories and comparisons between them. I'm sure I'm missing some, so please help!

    • Discussion resumes at the bottom of graph.

    • I made a UC Riverside Seminar on Cobordism and Topological Field Theories page to record all the notes from the seminar. Kind of like a seminar webpage, but in the nLab. Heh, I'm at home so I can't post comments to the n-category cafe (I'm trying to sort this out, my computer is not allowed to post comments currently).
    • I got tired off looking at a question mark on my personal web and added a stub for Hilbert schemes.

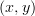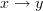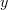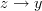    • I weakened the definition of covering relation for directed graphs so that (x,y) satisfy the covering relation if their is an edge x\to y and no other path from x to y. The condition that there is no z with edges x\to z and z\to y is too strong.

    • This comment is invalid XML; displaying source. Following discussion here <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=244&page=1#Item_3" >here</a>, I decided it made sense to have an <a href="http://ncatlab.org/nlab/show/FAQ#how_can_i_get_a_personal_section_of_the_nlab_14" >FAQ entry on personal pages.</a> It doesn't say much at the moment, but I guess the only important piece of information is that you have to write Urs.

    • created pages for Tony Pantev and Ludmil Katzarkov

      (not much there yet, am just following the idea that it would be nice that most authors whose references are cited in some entry also have a page with at least a link to their website)

    • I added the case of Set-enriched category theory to the example section of Cauchy complete category (thanks to David Corfield for fixing my LaTeX errors), and inserted the definition at Karoubi envelope. There is an issue of choosing how to split idempotents which someone like Toby might want to say something about.

    • created page for Johan Louis Dupont, cited at simplicial deRham complex

      (given that at that entry I am trying to merge some of Dupont's work with some of that of Anders Kock, it is curious that JL Dupont and Anders Kock are decade-long colleagues in Aarhus, as Anders Kock kindly reminds me a minute ago)

15061 to 15120 of 15187

  1. <
  2. 1
  3. ...
  4. 246
  5. 247
  6. 248
  7. 249
  8. 250
  9. 251
  10. 252
  11. 253
  12. 254
  13. >
Top of Page