nForum
Not signed in
Want to take part in these discussions? Sign in if you have an account, or apply for one below
Site Tag Cloud
Vanilla 1.1.10 is a product of Lussumo. More Information: Documentation, Community Support.
If you want to take part in these discussions either sign in now (if you have an account), apply for one now (if you don't).
-
- CommentRowNumber1.
- CommentAuthorEric
- CommentTimeNov 5th 2009
Asked a question at functor.
-
- CommentRowNumber2.
- CommentAuthorUrs
- CommentTimeNov 5th 2009
I wrote a quick reply
-
- CommentRowNumber3.
- CommentAuthorUrs
- CommentTimeNov 5th 2009
I think what you (Eric) are now looking for is the notion cograph of a functor -- somebody should write out the details of what a cograph looks like more in detail there. It does appear in the proof of the adjunciton statement, but should appear earliere independently.
But it won't be me. I'll have to sleep now! :-)
-
- CommentRowNumber4.
- CommentAuthorEric
- CommentTimeNov 6th 2009
Gave a second attempt at an alternative definition of functor. I think this is a little better than the last one.
-
- CommentRowNumber5.
- CommentAuthorUrs
- CommentTimeNov 7th 2009
Eric,
I just posted a reaction there. I don't get what you are after.
The standard definition of functor is entirely non-mysterious and obvious it seems. What is it that you would like to change?
Could it be that you are getting distrcacted by the internal definition of functor that we list on that page, too? Which involves lots of diagrams? Are you happy with the "external" ordinary definition that the entry starts with?
-
- CommentRowNumber6.
- CommentAuthorTodd_Trimble
- CommentTimeNov 7th 2009
It's not that I mind Eric speculating aloud, but could we clearly designate such discussions within pages as "Sandbox" discussions? These sandbox discussions are beginning to spill across pages and I'd prefer seeing greater containment.
-
- CommentRowNumber7.
- CommentAuthorEric
- CommentTimeNov 7th 2009
Yeah, Todd. I agree. I've suggested creating something like functor (discussion) or even functor (sandbox) would be fine. I don't want my questions to distract from what should be a simple concise page functor.
I asked here before just doing it because I thought we might want to agree on some standard format, but I just created
and
natural transformation (discussion)
and moved the long discussions from functor and natural transformation.
-
- CommentRowNumber8.
- CommentAuthorMike Shulman
- CommentTimeNov 7th 2009
Or even something like proposed alternate definition of functor, to be more descriptive.
-
- CommentRowNumber9.
- CommentAuthorEric
- CommentTimeNov 7th 2009
I was to move the functor stuff to "proposed alternative definition of functor", but before I do that I thought I would ask if the nLab is the right place for it, or should I move it to my personal web? I don't expect anyone to visit my personal web (although I hope they do!). I usually try to work stuff out on my personal web until it is 1/4 baked and then ask on the nLab where someone might actually see it.
-
- CommentRowNumber10.
- CommentAuthorTodd_Trimble
- CommentTimeNov 7th 2009
I even prefer "experimental alternative definition of functor" because "proposed" sounds as if it's been in the oven for a while, or at least "proposition" conveys to me seriously deliberated intent. Both the natural transformation and functor discussions seem much more tentative and experimental than that.
I think the nLab is a fine place for that, but I would like clearly marked indications that such pages have a different status than others. They are not controversial precisely; they're just brainstorming.
-
- CommentRowNumber11.
- CommentAuthorEric
- CommentTimeNov 7th 2009
- (edited Nov 7th 2009)
Thanks. I moved functor (discussion) to experimental alternative definition of functor. I hope that is alright.
Note: By "alternative" I mean "alternative, yet equivalent", i.e. I'm not trying to redefine what a functor is, but trying to understand it in a different way that works better with the way my brain is wired.
Edit: I'll also rename natural transformation (discussion) once I have a better handle on exactly what I'm trying to do. Now, I'm thinking that I should be saying "3-morphism" or something.
-
- CommentRowNumber12.
- CommentAuthorTobyBartels
- CommentTimeNov 8th 2009
@ Eric #9:
I read your personal web; does anybody else?
-
- CommentRowNumber13.
- CommentAuthorTodd_Trimble
- CommentTimeNov 8th 2009
Added a verbose comment to discussion at experimental alternative definition of functor. A shorter question to Eric is "add components how?" -
- CommentRowNumber14.
- CommentAuthorEric
- CommentTimeNov 9th 2009
Thank you very much Todd for taking the time to respond. I know it probably doesn't make much sense, but this is the way I HAVE to learn things. It really is my problem and I'm not saying there is anything wrong with traditional definitions. In my mind, this SHOULD work, and if it doesn't work, it means my knowledge is so far insufficient (obviously!).
I am confused though, but I'll post some thoughts/questions there.
Thanks again!
-
- CommentRowNumber15.
- CommentAuthorUrs
- CommentTimeNov 9th 2009
I reacted at experimental alternative definition of functor to Todd's reaction by repeating my previous suggestion that all does make sense here in the context of cograph of a functor.
-
- CommentRowNumber16.
- CommentAuthorTodd_Trimble
- CommentTimeNov 9th 2009
Agreement with Urs at experimental alternative definition of functor.
Whinge: I wish reCaptcha were more legible and used only recognizable words. -
- CommentRowNumber17.
- CommentAuthorUrs
- CommentTimeNov 9th 2009
Thanks, Todd. Concerning Eric's remark: it is true that the discussion at cograph could give more details and better explanation. I think this would be a good place for Eric make people spell out more details there.
-
- CommentRowNumber18.
- CommentAuthorUrs
- CommentTimeNov 9th 2009
- (edited Nov 9th 2009)
I added a section "With special properties" and a section "Generalizations" to functor.
Eric, you are now asking for a definition of functors in terms of cographs. At cograph of a functor it is indicated how cograophs encode profunctors, which are a bit more general than functors. That is the route how functors may be defined in terms of categories equipped with a map to the interval category.
I am just saying this to indicate the road map. I agree that it would be good to describe this in more detail.
I think your graphics could go pretty much as is currently to cograph of a functor and would be a very useful addition there.
-
- CommentRowNumber19.
- CommentAuthorEric
- CommentTimeNov 9th 2009
Thank you Urs. I believe that thinking about things this way is probably an easier introduction for "scientists and engineers". It is neat how it seems to carry through naturally for various degrees. For example, we have 1-profunctors and 0-profunctors. How about (-1)- and (-2)-profunctors? Toby? :)
I'm still EXTREMELY foggy on the concepts, but I feel a sudden improvement in focus.
-
- CommentRowNumber20.
- CommentAuthorUrs
- CommentTimeNov 9th 2009
- (edited Nov 9th 2009)
The trouble is that at cograph of a functor the simple definition isn't at the moment spelled out at the beginning. It is hidden in the proof of that proposition a bit further down.
Somebody should try to start writing a description of what a cograph of a functor is for scientists and engineers.
(Sorry for saying "somebody should", but I can't at the moment...)
-
- CommentRowNumber21.
- CommentAuthorUrs
- CommentTimeNov 9th 2009
I added some more examples to functor
-
- CommentRowNumber22.
- CommentAuthorTobyBartels
- CommentTimeNov 9th 2009
@ Todd #16 (OT)
ReCaptcha always uses one word which is recognisable and legible and one word which may not be recognisable and legible. And it is only the recognisable and legible word that you have to get correct!
(To be more specific, it uses one word which was recognised and read by a computer before it was distorted, and one word which the computer could not recognise and read, even before it was distorted. If you find that you can recognise and read the other word after all, then you are helping the computer to digitise books.)
-
- CommentRowNumber23.
- CommentAuthorTodd_Trimble
- CommentTimeNov 9th 2009
The entry for cograph of a functor starts off pretty scary, it seems to me. I'd ease into it much more gently. I'll see if I can say something more specific and constructive soon (not having a lot of time right now either). -
- CommentRowNumber24.
- CommentAuthorTodd_Trimble
- CommentTimeNov 9th 2009
I added a query box at the beginning of cograph of a functor to suggest some of my thoughts for rewriting it. I can add more later.
@Toby: my problem is sometimes both words are fairly illegible, and I have to refresh several times before I feel confident I'll get either one right. -
- CommentRowNumber25.
- CommentAuthorUrs
- CommentTimeNov 9th 2009
- (edited Nov 9th 2009)
Thanks, Todd!
Yes, your suggestion looks good. You should feel free to go ahead and implement it.
The reason it started off scary was because I created it at some point together with graph of a functor just to indicate that the concepts exist and have useful applications. This arose in some discussion. So the state of the entry isn't meant to be indicative of how such an entry should eventually look like.
-
- CommentRowNumber26.
- CommentAuthorEric
- CommentTimeMar 27th 2010
- (edited Mar 27th 2010)
By the way, I believe I found a way to express my alternative definition in a clean way that does not resort to non-standard morphism-like maps
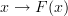 or cographs. Basically it goes like this...
or cographs. Basically it goes like this...Given categories
 and
and  , a map
, a map 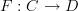 is a functor if for every morphism
is a functor if for every morphism 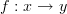 in
in  we have
we have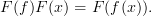
I gave my best attempt at a proof on the page experimental alternative definition of functor.
-
- CommentRowNumber27.
- CommentAuthorUrs
- CommentTimeMar 27th 2010
- (edited Mar 27th 2010)
What is
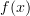 in your notation ?!
in your notation ?!I can dream up a good way to make sense of this, please think about it and let me know which pieces are unclear:
Namely here is the deal: a morphism
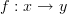 in a category is just abstractly an arrow from here to there. If the category is that of sets and functions, then the morphism will denote an actual function that takes elements
in a category is just abstractly an arrow from here to there. If the category is that of sets and functions, then the morphism will denote an actual function that takes elements  in the set
in the set  to elements in
to elements in 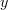 , but for a general category no such mapping of elements is a priori in the definition.
, but for a general category no such mapping of elements is a priori in the definition.But a beautiful fact is that there is always a way to look at the situation such that it does become of this form: every morphism in any category is a genuine map of sets of elements -- but of generalized elements.
A generalized element of an object
 in a category is just another word for any morphism with codomain
in a category is just another word for any morphism with codomain  , i.e. any morphism of the form
, i.e. any morphism of the form 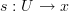 .
.The set of all such morphisms into
 is taken by a morphism
is taken by a morphism 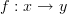 to the set of all such generalized elements of
to the set of all such generalized elements of 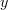 . How? By composition:
. How? By composition: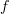 sends the generalized element
sends the generalized element 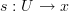 of
of  to the generalized element
to the generalized element 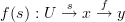 of
of 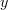 .
.Do you see what I mean?
If we do adopt this notation of
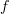 acting on generalized elements, then it does become true that some
acting on generalized elements, then it does become true that some 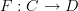 is a functor if for
is a functor if for 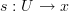 any generalized element of
any generalized element of  in the category
in the category 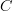 and
and 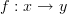 any morphism in
any morphism in 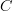 we have
we have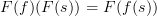 .
.That's because this equation of generalized elements is by definition the following equation between just morphisms and their composites:
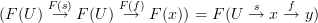
and this is the defining condition on a functor!.
-
- CommentRowNumber28.
- CommentAuthorEric
- CommentTimeMar 27th 2010
- (edited Mar 27th 2010)
Neat! Thank you Urs.
Let me repeat that using my words to make sure I get it...
My latest incarnation was "closer" but not quite good enough because it relied on their being some "
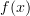 ". Apparently, this needs a refinement. The refinement involves generalized elements. Instead of
". Apparently, this needs a refinement. The refinement involves generalized elements. Instead of  , I need a generalized element
, I need a generalized element 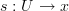 .
.Then we CAN define a functor as a map
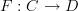 such that for all morphisms
such that for all morphisms 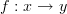 and all generalized elements
and all generalized elements 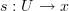 in
in 
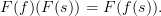
This makes perfect sense and is beautiful :)
Can we promote this to the nLab? For example, can I add a section "In terms of generalized elements" to functor?
-
- CommentRowNumber29.
- CommentAuthorUrs
- CommentTimeMar 27th 2010
Yes, you got it.
Can we promote this to the nLab?
Done:
Functors and generalized elements
(I also edited the rest of the entry a bit. Also expanded the Idea-section.)
-
- CommentRowNumber30.
- CommentAuthorEric
- CommentTimeMar 27th 2010
- (edited Mar 27th 2010)
Awesome.
I added a diagram to accompany the new section.
In drawing the diagram, I now see that probably the most succinct way to say what I've been trying to say is:
Definition:
Given categories
 and
and  , a functor
, a functor 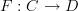 is a map that sends every commuting diagram in
is a map that sends every commuting diagram in  to a commuting diagram in
to a commuting diagram in  .
.How does that sound?
-
- CommentRowNumber31.
- CommentAuthorEric
- CommentTimeMar 27th 2010
- (edited Mar 27th 2010)
PS:
Commuting Diagram #1:
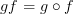
In order for this commuting diagram in
 to map to a commuting diagram in
to map to a commuting diagram in  , we need
, we need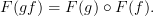
Commuting Diagram #2:
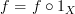
In order for this commuting diagram in
 to map to a commuting diagram in
to map to a commuting diagram in  , we need
, we need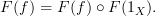
THIS, I believe, is the clean (yet equivalent) statement I've been looking for all along.
-
- CommentRowNumber32.
- CommentAuthorFinnLawler
- CommentTimeMar 27th 2010
That's exactly right, as long as you take
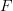 's action on a diagram in
's action on a diagram in  to be the composite in
to be the composite in  of
of 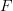 's action on each individual arrow in the diagram, and not
's action on each individual arrow in the diagram, and not 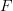 applied to the composite in
applied to the composite in  (which would make the definition trivial). I'm sure that's what you had in mind, though.
(which would make the definition trivial). I'm sure that's what you had in mind, though. -
- CommentRowNumber33.
- CommentAuthorHarry Gindi
- CommentTimeMar 27th 2010
Eric, this definition is the standard definition!
-
- CommentRowNumber34.
- CommentAuthorEric
- CommentTimeMar 27th 2010
- (edited Apr 22nd 2010)
@Finn: Yep yep. That is what I meant.
@Harry: I never said I wanted to create some new concept and call it "functor". I wanted to find a different wording for the definition that was equivalent, yet more pleasing to me personally.
Definition #1:
Given categories
 and
and  , a functor
, a functor 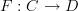 is a map that sends each object
is a map that sends each object  in
in  to an object
to an object 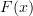 in
in  and each morphism
and each morphism 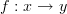 in
in  to a morphism
to a morphism 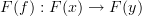 in
in  such that:
such that: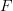 preserves compositions,
preserves compositions,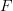 preserves identities.
preserves identities.
Definition #2:
Given categories
 and
and  , a functor
, a functor 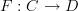 is a map that sends each object
is a map that sends each object  in
in  to an object
to an object 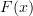 in
in  and each morphism
and each morphism 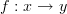 in
in  to a morphism
to a morphism 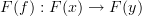 in
in  such that each commuting diagram in
such that each commuting diagram in  maps to a commuting diagram in
maps to a commuting diagram in  .
.
Of the two, in my opinion, Definition #2 is more motivated than Definition #1, although it is easy to show the two are equivalent.
-
- CommentRowNumber35.
- CommentAuthorHarry Gindi
- CommentTimeMar 27th 2010
if (ab)c=a(bc) is harder for you to visualize than the diagram expressing it, then you're not visualizing it right.
-
- CommentRowNumber36.
- CommentAuthorEric
- CommentTimeMar 27th 2010
I'll keep that in mind. Thanks! :)
-
- CommentRowNumber37.
- CommentAuthorEric
- CommentTimeMar 28th 2010
Since I am fairly fond of this "equivalent yet worded differently" definition of functor, I added a few more prominent sentences and a new diagram to the "External Definition".
An expert might want to give it their blessing though because I am a little confused why in the standard definition, we need to expressly state the condition about identities because it seems to me that it follows from the first statement about compositions. So the reason why we need that second statement about identities could be a source for some needed refinement in what I wrote.
Please have a look at functor
-
- CommentRowNumber38.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
I can think up a really strange situation where it does not imply it.
Consider an endomorphism that is a partial identity of the object so that when composed with all morphisms of a certain subclass, it acts as the identity, but it acts differently on morphisms outside of that class.
now consider a map into this category where for all morphisms f, F(f) belongs to this class.
Then map the identity to this endomorphism.
Then given the definition without the identity maps to identity axiom, this is a functor, but it is not under the standard defintion.
Edit: A better one as follows.
Fix a monoid M with a subset P with a partial identity, i.e., P is closed under multiplication and there is an element x in P such that xa=ax=a for all a in P, but suppose that x is not the identity of M. Then the inclusion of P in M is not a homomorphism, and similarly the induced map on deloopings is not a functor, although it satisfies the composition criterion.
The classic examples of this usually happen in a ring-theoretic context where nontrivial idempotents often exist, but the delooping statement is easier to explain for a raw monoid. The only difference in the case of a ring would be to further require additive enrichment.
The good part about this example is that since there is only one object, we can be totally explicit about what's going on.
For example, consider the following commutative ring: Q x Q (Q is the rational numbers)
Then Q is also a ring, but the set Q x {0} is not a subring although it is technically itself a ring. If we look at the inclusion Q x {0} ->QxQ and look at the deloopings, this gives an explicit example where identity does not map to identity.
Edit 2:
Here's a formula to come up with a wealth of other examples for monoids: Let i be a nontrivial idempotent of a monoid M. Then consider the set {ixi:x is in M}. Then this set is equipped with a submagma structure, and it is in fact a monoid by inspection. However, it is not a submonoid because identity does not map to identity. QED.
-
- CommentRowNumber39.
- CommentAuthorMike Shulman
- CommentTimeMar 28th 2010
Just to avoid any possible confusion: In #38 I think all occurrences of the word "automorphism" should be "idempotent."
Of the two, in my opinion, Definition #2 is more motivated than Definition #1, although it is easy to show the two are equivalent.
Interesting. This can be viewed as another instance of the biased/unbiased dichotomy. It's my view that unbiased notions are always the "right" ones, and biased ones are only correct insofar as they can be shown to be equivalent to unbiased ones. But for some reason a lot of people find it easier to think about biased definitions as "the" definition. This already appears in basic abstract algebra, e.g. a group homomorphism is usually defined as a map which preserves composition and identities (and in that case, it really does follow that the first implies the second), but "really" it is a map which preserves n-ary composites for all n.
-
- CommentRowNumber40.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
Yes, endomorphism. My mistake! I've fixed it.
Edit:
Mike, the reason why it is more common in algebra to do this is because strict associativity gives you this freedom. In fact, Bourbaki treats the very beginning of algebra using unbiased n-ary composites. It's in chapter 1 of Algebra. It's actually quite interesting, because they prove a number of things about index-arithmetic which are nice to know (yes, literally arithmetic on indices).
-
- CommentRowNumber41.
- CommentAuthorEric
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
Sorry. This seems interesting, but a little over my head.
Did Harry show that Definition #2 and Definition #1 are not equivalent? Or just that Definition #1 requires the statement about identities?
I'm also interested in Mike's dichotomy. I'm still not 100% clear whether Definition #2 is a good definition or if its flawed. If it is good, I'm not sure it implies it is biased or unbiased. I don't think I would ever choose one equivalent definition over another one as being "the right" one, but I would choose one definition over another as "being right for me". We all have our biases and those biases determine which definition among choices is "right" for them. It is an interesting question whether you could formalize what "right" means.
My bias is that I'd like to do as much as I can with pictures and as few words as possible.
-
- CommentRowNumber42.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
My examples showed teh necessity of the identity axiom.
-
- CommentRowNumber43.
- CommentAuthorEric
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
If
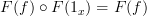 for all morphisms in
for all morphisms in 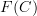 out of
out of 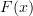 and
and 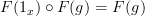 for all morphisms in
for all morphisms in 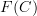 into
into 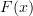 , then wouldn't that mean
, then wouldn't that mean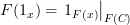 ?
?So is the issue that
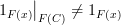
for morphisms not in
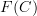 ? If so, then I don't understand why that matters. This is probably the source of my confusion. Why does it matter?
? If so, then I don't understand why that matters. This is probably the source of my confusion. Why does it matter?PS: Since Definition #2 does not have an explicit identity axiom, does that mean it is not equivalent to Definition #1? A yes or no would be helpful. I'm still not sure whether Definition #2 is correct. If not, I need to remove some lines from functor.
PPS: For example, without the identity axiom, then
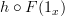 may not equal
may not equal 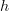 if
if 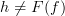 for some
for some 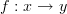 in
in  , but why does that matter? As long as
, but why does that matter? As long as 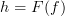 for some
for some 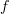 , then we always have
, then we always have 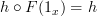 .
. -
- CommentRowNumber44.
- CommentAuthorEric
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
Sorry. I'm slow.
I think Definition #2 is the same as Definition #1 if you neglect the identity axiom, so Definition #2 is not complete.
By the way, Definition #2 is stated almost word-for-word (with the same variable names!) in Goldblatt to explain the preserving compositions condition.
-
- CommentRowNumber45.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
You an have morphisms called partial identities that act like identities but aren't.
-
- CommentRowNumber46.
- CommentAuthorEric
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
Thanks Harry.
From what I understand (which is little and often incorrect), some authors historically defined categories purely in terms of morphisms (I think), where the identity morphisms were identified with objects (or something). Could that explain why we want
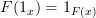 on the nose? In other words, if
on the nose? In other words, if  really is the same as
really is the same as 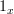 , then of course we want
, then of course we want 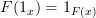 because it is essentially the same as saying
because it is essentially the same as saying 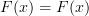 :)
:)See what I mean?
Edit: From wikipedia:
From these axioms, it can be proved that there is exactly one identity morphism for every object. Some authors deviate from the definition just given by identifying each object with its identity morphism.
-
- CommentRowNumber47.
- CommentAuthorMike Shulman
- CommentTimeMar 28th 2010
@Harry #40: I don't think strictness has much to do with it; if anything, unbiased versions are even more easier in the weak world.
@Eric: I would consider your definition #2 to be unbiased, and to include definition #1. The two axioms in definition #1 are both particular sorts of commuting diagrams: a composition of arrows is a commuting triangle, and an identity is a commuting loop.
-
- CommentRowNumber48.
- CommentAuthorEric
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
Oh! Thanks Mike. That is great. I had second thoughts, so removed a statement I made at functor. I'll roll it back.
That is a neat point about
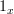 being a commuting loop. I hadn't thought of it that way (and I doubt Goldblatt did either or he probably would have mentioned it when he mentioned composition was a commuting triangle).
being a commuting loop. I hadn't thought of it that way (and I doubt Goldblatt did either or he probably would have mentioned it when he mentioned composition was a commuting triangle). -
- CommentRowNumber49.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
@Mike: It needs to preserve more than all commutative diagrams. It must preserve identities as well. (This is strictly stronger, as I've just shown.)
-
- CommentRowNumber50.
- CommentAuthorEric
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
@Harry: The point is that identities ARE commuting diagrams. That is pretty neat.
PS: I've now updated functor to reflect all this.
-
- CommentRowNumber51.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
You do not understand my example then. I've just given you an example where all diagrams commute but it is not an identity.
-
- CommentRowNumber52.
- CommentAuthorEric
- CommentTimeMar 28th 2010
Your example demonstrates nicely that "preserving composition" is not strong enough.
But "preserving commutative diagrams" is strong enough because composition is a commutative triangle and identities are commutative loops.
Bask in the beauty. This is kind of neat :)
-
- CommentRowNumber53.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
No. You're totally and categorically incorrect. Bask in the... I dunno... wrongness of your assertion.
Any nontrivial idempotent is a commuting loop as well =p.
-
- CommentRowNumber54.
- CommentAuthorEric
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
Sorry Harry. You must not have gotten enough sleep :)
Any commuting loop must be equal to the identity by definition. Consider an idempotent
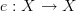
and the diagram consisting of one object
 and and two morphisms
and and two morphisms 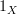 and
and  .
.For this diagram to commute, it would mean
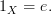
Plus, as an old man, I've learned there is rarely any benefit to accusing someone else of being wrong (especially in public). There is only downside risk to such statements.
-
- CommentRowNumber55.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
You must not have gotten enough sleep..
Just because you put LaTeX in there does not make it correct.
-
- CommentRowNumber56.
- CommentAuthorEric
- CommentTimeMar 28th 2010
The fact I haven't gotten enough sleep is usually a given :)
Please have another look. The basic fact here is that any commuting loop must be an identity. Do you agree with that?
-
- CommentRowNumber57.
- CommentAuthorEric
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
Here is the diagram I described above in pictures:
 [bummer: lefttorightarrow does not parse here though it does at the nLab. The picture is basically two loops
[bummer: lefttorightarrow does not parse here though it does at the nLab. The picture is basically two loops 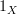 and
and  coming out of
coming out of  .]
.]Stating this diagram commutes is the same thing as stating
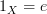 . This is true for any loop regardless of whether it is an idempotent.
. This is true for any loop regardless of whether it is an idempotent. -
- CommentRowNumber58.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
If you map an identity to an idempotent, then all diagrams still commute.
No, I don't agree that a commuting loop is the identity.
A loop is just any endomorphism.
Anyway, even if it were, it still does not address what I said.
If you map the identity to a nontrivial idempotent then all diagrams still commute.
-
- CommentRowNumber59.
- CommentAuthorEric
- CommentTimeMar 28th 2010
<p>Speaking of lack of sleep, it is close to 1:30am here in HK so I'm going to hit the sack soon. Just some parting notes:</p> <p><a href="https://ncatlab.org/nlab/show/experimental+alternative+definition+of+functor">experimental alternative definition of functor</a></p> <p>Let's consider a category <img src="/extensions/vLaTeX/cache/latex_ca43fb5496104dcafda44acbe4014b0e.png" title="C" style="vertical-align:-20%;" class="tex" alt="C" /> with two objects <img src="/extensions/vLaTeX/cache/latex_04d0eb37f084cb02c47fa2a271035fef.png" title="X" style="vertical-align:-20%;" class="tex" alt="X" /> and <img src="/extensions/vLaTeX/cache/latex_4dc4f99626c3d159bf0a8ca65ee0e5e3.png" title="Y" style="vertical-align:-20%;" class="tex" alt="Y" /> and two non-identity morphisms <img src="/extensions/vLaTeX/cache/latex_703bca9bbf49947bbfea319ffe4929b7.png" title="f:X\to Y" style="vertical-align:-20%;" class="tex" alt="f:X\to Y" /> and <img src="/extensions/vLaTeX/cache/latex_87b5da867a9a34ae700a0905c3cf18f4.png" title="g:Y\to X" style="vertical-align:-20%;" class="tex" alt="g:Y\to X" />. By declaring this diagram commutes, we are saying</p> <img src="/extensions/vLaTeX/cache/latex_f879b26adb445e3f09c31c9c3f814014.png" title="g\circ f = 1_X" style="vertical-align:-20%;" class="tex" alt="g\circ f = 1_X" /> <p>and</p> <img src="/extensions/vLaTeX/cache/latex_73c442c9e4cf3906c12f62f223cd2aa9.png" title="f\circ g = 1_Y." style="vertical-align:-20%;" class="tex" alt="f\circ g = 1_Y." /> <p>A map <img src="/extensions/vLaTeX/cache/latex_4ab4a8e1b1343def201689148996e8cd.png" title="F:C\to D" style="vertical-align:-20%;" class="tex" alt="F:C\to D" /> from this category to any other category that "preserves commuting diagrams" sends these two equations to</p> <img src="/extensions/vLaTeX/cache/latex_0d21ffba5b7b0ec9f05a73ef16c2d60e.png" title="F(g)\circ F(f) = 1_{F(X)}" style="vertical-align:-20%;" class="tex" alt="F(g)\circ F(f) = 1_{F(X)}" /> <p>and</p> <img src="/extensions/vLaTeX/cache/latex_68a93e879d75bee1d4056affe71f5ab4.png" title="F(f)\circ F(g) = 1_{F(Y)}" style="vertical-align:-20%;" class="tex" alt="F(f)\circ F(g) = 1_{F(Y)}" /> <p>due to the fact the two loops must commute and must therefore equal the identity. Since the LHS's also map to <img src="/extensions/vLaTeX/cache/latex_fa4650b3477c45ce7c902c18a7dde49e.png" title="F(1_X)" style="vertical-align:-20%;" class="tex" alt="F(1_X)" /> and <img src="/extensions/vLaTeX/cache/latex_6f7698e0a51cb5fdbfb0313ce12b2a54.png" title="F(1_Y)" style="vertical-align:-20%;" class="tex" alt="F(1_Y)" /> respectively, we have</p> <img src="/extensions/vLaTeX/cache/latex_6f25d68c9c91a8f905a8b4e385d60771.png" title="F(1_X) = 1_{F(X)}" style="vertical-align:-20%;" class="tex" alt="F(1_X) = 1_{F(X)}" /> <p>and</p> <img src="/extensions/vLaTeX/cache/latex_ee51ae21e48ba564cfdafc1471bda749.png" title="F(1_Y) = 1_{F(Y)}." style="vertical-align:-20%;" class="tex" alt="F(1_Y) = 1_{F(Y)}." /> <p>For a reference, see this exact same example on <a href="http://mathworld.wolfram.com/CommutativeDiagram.html">Mathworld</a>.</p> <p>The sticking point seems to be that you do not agree that a commuting loop must equal the identity. I don't know what to say about that except to please have another look at what it means for a loop to commute. It means it is equal to the identity.</p> <p>I didn't get that at first either, but had my EUREKA moment <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=1000&Focus=7144#Comment_7144">here</a>.</p> -
- CommentRowNumber60.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
- (edited Mar 29th 2010)
Edit: I said something stupid that I've removed.
Please refrain from lecturing me on functors.
-
- CommentRowNumber61.
- CommentAuthorEric
- CommentTimeMar 28th 2010
No, I don't agree that a commuting loop is the identity.
Hmm... maybe an authoritative voice can help? Urs? Mike? David?
A loop begins at one object
 and ends at same object. However, there is always a second loop also coming from
and ends at same object. However, there is always a second loop also coming from  , i.e.
, i.e. 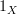 . So to say a loop commutes means that it commutes with
. So to say a loop commutes means that it commutes with 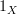 and for it to commute with
and for it to commute with 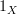 , it must equal
, it must equal 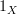 .
.In a way, I hope I am wrong...
-
- CommentRowNumber62.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
A contractible loop is homotopic to the constant loop, but what you're saying doesn't mean anything...
-
- CommentRowNumber63.
- CommentAuthorEric
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
No, you're absolutely mistaken. It is not necessary for a loop to map to a loop.
Valient effort, but as stated at functor, i.e. if
 -objects
-objects  map to
map to  -objects
-objects 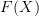 and
and  -arrows
-arrows 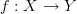 map to
map to  -arrows
-arrows 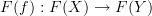 , then most certainly loops will map to loops.
, then most certainly loops will map to loops. -
- CommentRowNumber64.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
False. A loop that is contractible in the domain need not be contractible in the range.
-
- CommentRowNumber65.
- CommentAuthorEric
- CommentTimeMar 28th 2010
2am. Really time for me to sleep. It's been fun being able to spend some time on this stuff. I hope you eventually learn to like Definition #2, but no worries either way. I'm very happy.
Now I need to go back to the real world for a while. Thanks for the escape! Good night :)
-
- CommentRowNumber66.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
I hope that you one day realize that you're incorrect.
-
- CommentRowNumber67.
- CommentAuthorEric
- CommentTimeMar 28th 2010
False. A loop that is contractible in the domain need not be contractible in the range.
True, but it is still a loop :)
-
- CommentRowNumber68.
- CommentAuthorEric
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
I hope that you one day realize that you're incorrect.
Don't worry. I realize that I'm incorrect multiple times each day and I'm ok with that. I hope you can become ok with mistakes as well. Everyone makes them.
-
- CommentRowNumber69.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
Come back to me when you understand my counterexample.
-
- CommentRowNumber70.
- CommentAuthorEric
- CommentTimeMar 28th 2010
I will. Let's discuss it when you understand what a commuting loop is ;)
-
- CommentRowNumber71.
- CommentAuthorHarry Gindi
- CommentTimeMar 28th 2010
"Commuting loop" has no meaning unless you're defining it to mean contractible.
-
- CommentRowNumber72.
- CommentAuthorDavidRoberts
- CommentTimeMar 28th 2010
- (edited Mar 28th 2010)
I'm afraid, Eric, that a loop really only contains one arrow, and that for it commute all you're asking is that it is equal to itself. If you put in the implicit assumption that the identity arrow is hiding there, so that given an endomorphism f = id then after applying F:C -> D you just get F(f) = F(id). With no assumptions past definition #2, you don't know that any identities in D are even in the image of F, then it doesn't work to claim that since F(f) is an endomorphism it is necessarily equal to the identity in D, because the axiom in #2 is about preserving things that come from C.
I was going to respond to Harry's claim about the images of loops being non-contractible, but I realised that since topology does work like it should, fundamental groupoids/path categories are a bad analogy to use here. A better example to use, perhaps, is of maps or pointed sets. Consider a monoid or a group as a one-object category. Then a functor between them has to give rise to a _pointed_ map between the sets of arrows which are pointed sets by taking the identity element as the point. For this to work we need the point to be mapped to a point. As there is no algebra, we need to state this explicitly, and it is no different in the case for categories and functors. Somewhere in your reasoning, Eric, some assumption has slipped in I'm afraid.
Where the other are talking about unbiased definitions, the identities are preserved because they are 0-ary compositions of arrows, and unbiased definitions of functors require that compositions of strings of n arrows (for n greater or equal to 0) are preserved. Unless you make some caveats on what you mean a commuting diagram to be (and to me it seems you are) then the straight-up definition #2 is not strong enough.
To me saying a functor takes identities to identities, and preserves all commuting diagrams is not a bad compromise, because one is about composition and one is about identities, and in the definition of category the existence of these are taken separately.
Edit: I've just seen your other thread on commuting diagrams. IF (and that's a bold if) you take unadorned loops to be implicitly commuting diagrams with the invisible identity arrow, then I agree that the definition works, but I posit that this has to be included as a caveat before or after stating the definition, and you have not gained any parsimony for reducing the number of axions on functors. I guess it comes down to convetions. Anyway, I need to get ready for work, else I'll be late. Big shmozzle last week, got to find out if everything's gone to the dogs with the client. :) -
- CommentRowNumber73.
- CommentAuthorFinnLawler
- CommentTimeMar 28th 2010
It looks to me like this is just a disagreement over what a commutative diagram is. If asked I'd say that it's given by two paths (= composable sequences of arrows) whose composites are equal, so this debate seems to be over whether that includes the empty sequence, whose composite is the identity. I'd say it does. It's true that if you want to say that a path composes to 1 then you usually draw that arrow explicitly, but this seems to me to be a matter of disambiguation rather than mathematics: most people won't understand you if you say that a loop 'commutes', but that's because they don't know what the other path is that the loop is supposed to equal (because it's not shown).
David says:
IF (and that's a bold if) you take unadorned loops to be implicitly commuting diagrams with the invisible identity arrow, then I agree that the definition works, but I posit that this has to be included as a caveat before or after stating the definition, and you have not gained any parsimony for reducing the number of axions on functors.
Firstly, I think what this caveat amounts to is just an explanation of what the 'degenerate' cases of commuting diagrams are supposed to mean. I don't think it conflicts with any standard definitions. Secondly, I'm pretty sure Eric's after not parsimony but clarity.
-
- CommentRowNumber74.
- CommentAuthorHarry Gindi
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
Adopting a convention about degenerate cases of commutativity is bound to be harder to understand than explicitly stating it.
It's not really clear to me how you would even phrase such a convention in general.
-
- CommentRowNumber75.
- CommentAuthorDavidRoberts
- CommentTimeMar 29th 2010
<p>Actually, thinking about it on the train this morning, I find I agree with Eric. In practice (at least, until others tell me otherwise) I reckon that what Eric says about identity arrows in diagrams (here, and in the <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=1000&Focus=7144#Comment_7144">other thread</a>) is true. Just talking about a little arrow from a vertex to itself is degenerate and boring, but if you have a massive diagram, with a path around the page back to the source object, then saying this commutes is tantamount to saying this big composite is equal to the identity. If you are in a 2-category, then drawing a iso-2-arrow in a diagram from a composite to an object (and so the composite is necessarily an endo-1-arrow) means that the composite is isomorphic to the identity arrow (Urs' thesis has a lot of this :)</p> <p>Harry said:</p> <blockquote> <p>No, I don't agree that a commuting loop is the identity. ... A loop is just any endomorphism.</p> </blockquote> <p>this is almost like saying a commuting square is just a square diagram of arrows. By fiat we can say that a diagram with an endomorphism drawn (be it a composite of other stuff or no) commutes iff that endomorphism is the identity. This is a very handy convention if you ever need it.</p> <p>With my revised viewpoint, I'm afraid that experience of mathematical practice wins out, Harry. Having drawn a scad-load of big big diagrams (in bicategories and smaller) for computations, I hope you take my word for this.</p> -
- CommentRowNumber76.
- CommentAuthorHarry Gindi
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
There should be a way to express this diagrammatically then, and I can't see an easy way to do so.
Anyway, with degenerate cases like these, you must explicitly state the convention you are using.
Here's my issue: If you take a nontrivial idempotent, there is a diagram that commutes for it in that loop:
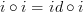 , or
, or 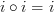
Then if you do not define commutativity, I've shown that this diagram commutes, and this diagram certainly has as much right to be called commutative as the other diagram.
-
- CommentRowNumber77.
- CommentAuthorEric
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
I'd be happy to say Harry and I were both right, but that it depends on how you define what it means for a degenerate loop, i.e. an endomorphism, to commute.
If it is a non-degenerate loop, i.e. involves more than one object, then to say it commutes means that it is equal to the identity. Regardless of how long the loop is. I don't think this is debatable. If you take this to include length = 1 (which seems logical), i.e. an endomorphism, then it means any commuting loop is equal to the identity.
If you draw a little "
 " (or "bowtie") diagram with a single object
" (or "bowtie") diagram with a single object  at the intersection and label the left loop
at the intersection and label the left loop 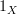 and the right loop
and the right loop  for any idempotent, then to say this diagram commutes means that
for any idempotent, then to say this diagram commutes means that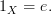
I suppose you might be able to define "commuting loop" such that loops of length 1 are treated differently than loops of length greater than 1, but then you'd have to have a very good reason for doing so I would think.
-
- CommentRowNumber78.
- CommentAuthorHarry Gindi
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
I don't see how that follows. What I'm saying is that "a commutative loop" has no meaning regardless of how many objects are involved unless you take the definition of it commuting to be that it is equal to the identity.
To say that a diagram commutes, it means that starting at a specific vertex, all concatenations of paths are equal. Then any graph with one vertex and one edge automatically commutes (this statement is vacuously true).
-
- CommentRowNumber79.
- CommentAuthorDavidRoberts
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
<p>(Edit: took a long time to write this, this was started after <a href="http://www.math.ntnu.no/~stacey/Vanilla/nForum/comments.php?DiscussionID=332&Focus=7186#Comment_7186">Harry's number 26 on this page</a>.)</p> <p>Hmm, I guess that it is convention that informs me: I would draw this as a triangle. and call it a commuting triangle. Drawing a diagram with two endomorphisms as loops on a single object is ambiguous unless they are the same, because we have no composition order. Likewise, saying 'these two endomorphisms compose to this third endomorphism, and I've drawn the object only once for simplicity' removes all content from the diagram, because we now know nothing about which endomorphisms to compose, in which order, or even if the composite of all three is the identity (as could be the case for the imaginary diagram corresponding to your idempotent). This is as the fuzzy edge of the formalism of diagram drawing, but one thing is for certain: no one should look at a diagram and not know in what order the composition happens.</p> <p>There is some ambiguity in drawing a square diagram with all arrows pointing clockwise, because one needs a start object. But, the point is, the diagram commutes, this can be clarified by words if necessary, and no one would argue. Unless you are proposing a project to create a formal diagrammatic language, I do not feel that debating the finer points of how to interpret diagrams with specially constructed examples if terribly useful for the present purposes ;)</p> <p>I do agree that convention would need to be established for definition #2 to make sense, but once it is established, it is useful (and is used in practice). This is what should inform choices of definitions. If Eric's alternative helps others to understand (in such a way they can put to use in practice) functors, then well and good. If padding needs to be inserted, then insert it. Most mathematical definitions come with padding, before or after, and most people are Bourbakian about it, formalising everything in definition sequences.</p> <p>Maybe only Eric will use his definition, and in private. He knows the official definition, but now has a grasp on what the definition of functor implies in practice, and how that practice can provide a working definition. I say good on him for persevering through criticism and his own false starts and so on. Everyone who does mathematics goes through times like this, longer or shorter, when absorbing new concepts. Do you criticise Grothendieck for writing huge swathes of stuff that is blatantly incorrect in Pursuing Stacks and sending it out for the world to read? Hardly. It was a work in progress. With the advent of tools like the nlab and this forum, the process of understanding and creating mathematics can be public, and with it comes the embarrassments of barking up the wrong tree. I wrote some shocking stuff on the Cafe when it was starting out, in an attempt to understand the Klein-2-geometry program in terms of categorified incidence geometry. I wasn't castigated, and I'm glad for that; my own shame was enough to make me try harder, I gained a lot of experience and I have a nice research program up my sleeve from insights gained in the process.</p> -
- CommentRowNumber80.
- CommentAuthorHarry Gindi
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
Absolutely. My point was that without explicitly establishing such a convention, the statement is nonsensical. My argument is not that such a convention would be a bad idea, merely that it is not an established convention and needs to be spelled out explicitly. If it is not, then Eric's definition does not suffice.
-
- CommentRowNumber81.
- CommentAuthorDavidRoberts
- CommentTimeMar 29th 2010
Well, some people (myself and Mike at least) think it is a semi-established convention at minimum, so I'm not so fussed.
-
- CommentRowNumber82.
- CommentAuthorDavidRoberts
- CommentTimeMar 29th 2010
And I agree (see my earlier posts) that without the convention the definition is not strong enough.
-
- CommentRowNumber83.
- CommentAuthorMike Shulman
- CommentTimeMar 29th 2010
I don't have time to read all the many comments on this thread carefully, but Finn, David, and Eric have taken my meaning correctly. Of course it depends on what is meant by a diagram "commuting," but the only general formal definition I know of for when a diagram "commutes" is that any two paths through it having the same starting and ending points have equal composites. (I guess for this to make sense one needs to first define a "diagram" as a map from a directed graph into a category.) And the path of length zero is just as good a path as any other path, and its composite is the identity, so in a commuting diagram any loop must be the identity. Likewise, in a commuting diagram any two parallel arrows must be equal.
On the other hand, we do sometimes want to talk about diagrams which don't commute in this sense, but in which any two parallel paths of length >1 have equal composites. For instance, the diagram defining an equalizer or coequalizer is of this form. Sometimes people say of such a diagram that it "serially commutes." But sometimes I think this phrase is also used in an even more general sense, and I'm not sure if it has any formal definition.
The word "diagram" also is sometimes used to mean an arbitrary functor (generally with very small domain). I would say that such a diagram "commutes" by definition, the requisite commutativities being specified by the compositions in the domain category. One could then say that a functor is a map of graphs which takes such "commutative" diagrams to commutative diagrams (not just to maps of graphs), although of course that is not suitable as a non-circular definition.
-
- CommentRowNumber84.
- CommentAuthorEric
- CommentTimeMar 29th 2010
Then there are probably concepts like "2-commute", i.e. an equalizer probably 2-commutes or something...
-
- CommentRowNumber85.
- CommentAuthorHarry Gindi
- CommentTimeMar 29th 2010
@Mike: That definition of commutativity works with the standard definition of a functor though.
-
- CommentRowNumber86.
- CommentAuthorEric
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
Attention is limited, but with a quick glance, I don't see any problem with equalizers and the alternative definition. With limits (in terms of universal cones), you do not specify that all diagrams commute together at once, but only that each individual diagram commutes. None of the diagrams are loops (by the way cones are constructed), so we bypass the issue of commuting loops.
I've likely misunderstood the concern (due to having no time)...
-
- CommentRowNumber87.
- CommentAuthorHarry Gindi
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
Defining a commuting diagram before defining a functor makes no sense to me, since diagrams are functors.
I mean, you can talk about diagrams by throwing out a lot of the categorical structure, but this is the whole point of the free category/diagram adjunction, which you need functors to define in the first place. It all just feels very imprecise to me, and to make it precise seems like it would require being circular.
-
- CommentRowNumber88.
- CommentAuthorEric
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
What's wrong with just saying a diagram is a subcategory?
Or maybe just defining what it means for a category to commute and not worry about diagrams?
Or maybe a little of both?
Or course we could change the definition of subcategory so instead of compositions and identities, it is about commuting diagrams :)
-
- CommentRowNumber89.
- CommentAuthorHarry Gindi
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
I don't know, why would we? That seems like an awful lot of trouble to go to...
-
- CommentRowNumber90.
- CommentAuthorDavidRoberts
- CommentTimeMar 29th 2010
Defining a commuting diagram before defining a functor makes no sense to me, since diagrams are functors.
ah, but the definition of functor (the usual one) only requires commuting diagrams of very small size: involving no more than three objects. This sort of thing can be defined by hand. However, Eric's definition #2 requires that all diagrams are preserved, and so we cannot use this argument. I'm not sure I can add much more here (and it is a terrible distraction at work :) except to say that some of this could be written up on a page unbiased definition of a functor, with the caveat we all agree is necessary to take care of identities.
-
- CommentRowNumber91.
- CommentAuthorEric
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
At the end of the day, wouldn't any commuting diagram reduce to the two simple cases: triangles (or even parallel morphisms) and loops?
For example, if you have parallel paths, one of length
 and one of length
and one of length 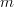 , these each reduce to paths of length one once you compose everything. So there are really only two cases you have to worry about and those are the same as compositions and identities.
, these each reduce to paths of length one once you compose everything. So there are really only two cases you have to worry about and those are the same as compositions and identities.If you have a loop of length
 , when you compose all morphisms, you end up with a loop of length 1.
, when you compose all morphisms, you end up with a loop of length 1.Or so I think :)
Edit: I'm pretty sure this statement is wrong, but I'll leave it. But I thought I would provide a link to Mathworld again. It is a nice little reference to come back to once in a while.
-
- CommentRowNumber92.
- CommentAuthorUrs
- CommentTimeMar 29th 2010
- (edited Mar 29th 2010)
Hi everybody,
a huge thread here has developed while i wasn't watching just for a little bit! I don't have quite the energy to read it now. But I looked at the additions to the entry. And these looks good!
Two remarks:
Given the pictures and discussion that is already there, maybe some of you might enjoy going further and discussing how functors between categories are in bijection with morphisms of simplicial sets between the corresponding nerves. I think this might shed light on the "meaning" of that issue of loops.
The two figures illustrating how a functor produces an image of a category in another category are very good. This is precisely the picture to draw and to have in mind. Just one minor remark: for full clarity, could we have the vertical dashed arrows that indicate where objects are sent be equipped with a little orthogonal line at their source, so as to be of the form "
 " instead of "
" instead of " ". That might help reduce the chance that somebody mixes these arrows up with the other arrows in the picture. Both are of crucially very different nature.
". That might help reduce the chance that somebody mixes these arrows up with the other arrows in the picture. Both are of crucially very different nature.
-
- CommentRowNumber93.
- CommentAuthorHarry Gindi
- CommentTimeMar 29th 2010
@Urs #1: Yes, this was the source for my statement about contractibility =).
-
- CommentRowNumber94.
- CommentAuthorDavidRoberts
- CommentTimeMar 30th 2010
@Eric (and Urs)
the simplicial description Urs mentioned occurred to me last night: one does need triangles, Eric, and this is reflected that a functor is the same thing as a map of truncated simplicial sets (truncated to dimension 2, or 3 to be safe): triangles are sent to triangles, and this is the same as preserving composition.
The whole issue of 'loops' (identity arrows) is possibly resolved by thinking of them as 0-ary composition. -
- CommentRowNumber95.
- CommentAuthorEric
- CommentTimeMar 30th 2010
Something occurred to me last night too, but it was in a dream, so you have been warned :)
The two important pieces in definitions relating to categories and functors are: compositions and identities.
Fundamentally, these are commuting triangles and commuting loops, respectively.
So what if we could define things directly in terms of these shapes? Something like, "A category is any shape that can be built from a collection of commuting triangles and commuting loops."
Composition is just a commuting triangle.
Identity is just a commuting loop (which can be identified with objects).
Associativity is just gluing two commuting triangles together.
The rule of the game is that if you glue any two commuting things together, you get a commuting thing.
Anyway, I haven't had my coffee yet. So there you go :)
-
- CommentRowNumber96.
- CommentAuthorDavidRoberts
- CommentTimeMar 30th 2010
This idea is, I think, contained in the result (of Grothendieck) that a category is a simplicial set such that (blah), where blah basically tells us that morphisms have a unique composite and this composition is associative and so on. The simplicial set is then the nerve of the category.
After the discussion we've had here, I advise against coming up with a new definition of category :) There are lots of nice ways to explain what a category is. -
- CommentRowNumber97.
- CommentAuthorEric
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
<blockquote> <p>After the discussion we've had here, I advise against coming up with a new definition of category :)</p> </blockquote> <p>Hehe :) You can guess I am not very good at taking advice like that, but I <strong><em>would</em></strong> like to learn about Grothendieck's result and see if it can be phrased in "high school" terms. Even elementary school kids could understand how to connect triangular puzzle pieces together.</p> <p>I know some people (present company excluded!) take pride in the fact the work they spend their days on is completely incomprehensible to the general population, but I still think that some of the basic results in category theory could be understood by my 4.5 year old daughter. There are two concepts that I think any kid who has seen an "=" sign could understand:</p> <ul> <li>Commuting triangles</i> <li>Gluing commuting triangles together</li> </ul> <p>I would be curious to see how much category theory could be built from those two simple concepts.</p> <p>Note: A commuting loop can be turned into a commuting triangle by replicating the object three times as Urs is fond of doing.</p> -
- CommentRowNumber98.
- CommentAuthorHarry Gindi
- CommentTimeMar 30th 2010
- (edited Mar 30th 2010)
Category theory is not the study of commuting diagrams. It's the study of objects by studying the morphisms between them. Higher category theory is the study of objects by studying the morphisms between the morphisms between the.... morphisms between the objects. Diagrams are a useful tool to do this, but they are a means rather than an end. If you want to study diagrams, you should check out homological algebra and read Peter Freyd's book on Abelian Categories.
-
- CommentRowNumber99.
- CommentAuthorMike Shulman
- CommentTimeMar 30th 2010
One thing that category theory does is study objects by studying the morphisms between them. But sometimes category theory studies morphisms by studying the objects they go between. And sometimes category theory studies commuting diagrams. I wouldn't say that there's any one thing of which category theory is the study, except perhaps "categories" (insofar as that is tautological).
-
- CommentRowNumber100.
- CommentAuthorEric
- CommentTimeMar 30th 2010
Is there anything remotely close to a reference for "scientists and engineers" that explains Grothendieck's results regarding simplices?